Определение . Точечной называют оценку, которая определяется одним числом.

Все оценки, рассмотренные выше, являются точечными. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Определение. Интервальной называют оценку, которая определяется двумя числами – началом и концом интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть 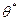 - это оценка неизвестного оцениваемого параметра 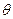. Пусть  - это некоторое положительное число. Если выполняется неравенство:

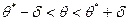, то говорят, что интервал  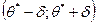покрывает неизвестный параметр .

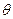Определение . Надежностью оценки  параметра 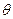 для заданного  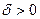называют вероятность того, что интервал  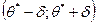покрывает параметр 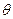, и обозначают в виде

.

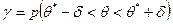Иными словами,  есть мера доверия вычисленной оценке .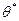

Определение . Доверительным интервалом называют найденный по данным выборки интервал 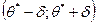, который покрывает неизвестный параметр  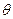с заданной надежностью .

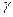Надежность 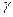 задается по условию задачи и обычно принимается равной 0,95, или 0,99, или 0,999.

Границы доверительного интервала и его длина находятся по выборочным данным, и являются случайными величинами. Величина доверительного интервала уменьшается с ростом объема выборки n и увеличивается с ростом доверительной вероятности γ. Если количественный признак генеральной совокупности X имеет нормальное распределение, то доверительный интервал для математического ожидания имеет вид:

, где 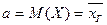- математическое ожидание;

- выборочная средняя;

- объем выборки;

 - при большом объеме выборки;

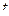- значение аргумента функции Лапласа, при котором она равна 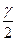, то есть 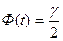, где 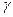- заданная надежность. Аргумент  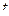находится по таблицам значений функции Лапласа (приложение 2).

Данная формула доверительного интервала математического ожидания будет справедлива только при большом объеме выборки, то есть если 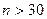. В противном же случае, равенство  не будет выполнятся и считают  неизвестной величиной.

Таким образом, если объем выборки не большой , то доверительный интервал для генеральной средней будет иметь вид:

,

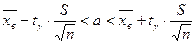где 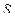 - это исправленное среднее квадратическое отклонение;

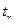 - это число, взятое из таблицы (приложение 3), и зависящее от объема выборки  и заданной надежности 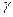, то есть .

Доверительный интервал для оценки среднего квадратического отклонения  вычисляется по формуле

,

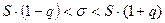где 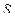 - это исправленное среднее квадратическое отклонение;

 - это табличное значение, которое зависит от объема выборки 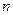 и заданной надежности 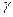, то есть  (приложение 4).

Пример. Найти интервальную оценку признака  генеральной совокупности, то есть доверительный интервал для математического ожидания, если известно, что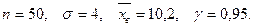  

Решение.

Для того чтобы воспользоваться приведенной выше формулой, найдем 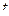 из равенства

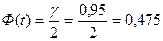, следовательно .

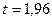Тогда, доверительный интервал будет иметь вид

;

; .

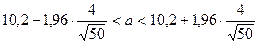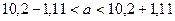Таким образом, с вероятностью 95% можно утверждать, что неизвестна генеральная средняя может находится в промежутке от 9,09 до 11,31.