В прикладных задачах часто требуется по эмпирическим данным проверить то или иное предположение. Например, используя полученную выборку, предполагают, что генеральная совокупность распределена по нормальному закону, или по показательному закону и т.д. Другими словами, выдвигают гипотезу: генеральная совокупность распределена по закону 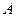, то есть речь идет о виде предполагаемого распределения.

Определение . Статистической гипотезой называют всякое высказывание о генеральной совокупности (случайной величине) проверяемое по выборке (по результатам наблюдений).

Например, статистическими являются гипотезы:

1) генеральная совокупность распределена по нормальному закону;

2) дисперсии двух нормальных совокупностей равны между собой;

3) математическое ожидание признака Х нормально распределенной генеральной совокупности равно 25,5.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Поэтому эти гипотезы принято различать.

Определение . Нулевой (основной) называют выдвинутую гипотезу и обозначаю 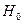, а гипотезу, которая противоречит нулевой, называют конкурирующей и обозначают в виде .

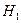Например, если 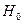- это математическое ожидание а нормального распределения равно 15, то конкурирующая ей гипотеза может состоять в предположении, что 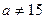. Коротко это записывают так: : ;

: .

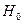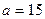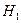Также различают гипотезы, которые содержат только одно и более одного предположения.

Определение. Простой называют гипотезу, содержащую только одно предположение, а сложной  называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Например, если 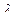- это параметр показательного распределения, то 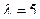- простая, а 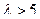- сложная гипотеза, так как состоит из бесконечного множества простых гипотез.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Так как проверку производят статистическими методами, то ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, то есть могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Последствия этих ошибок могут оказаться различными.

Например, пусть испытывается вновь созданный лекарственный препарат. Испытывая этот препарат, можно, например, выдвинуть гипотезу, что он в самом деле эффективен при лечении определенного заболевания. Если эта гипотеза верна, и она будет отвергнута, то эта ошибка первого рода, которая может привести к дальнейшему протеканию болезни. Если эта гипотеза не верна, но она будет принята, то это ошибка второго рода, которая тоже приведет к дальнейшему протеканию заболевания.

Замечание.

 1. Правильное решение может быть принято так же в двух случаях: 1) гипотеза принимается и в действительности она правильная; 2) гипотеза отвергается, причем и в действительности она не верна.

2. Вероятность совершить ошибку первого рода принято обозначать через , ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принять уровень значимости равный 0,05, то это означает, что в пяти случаях из 100 имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).