Задачи № 1-20. Используя классическое определение вероятности, решить задачу:
В лотереи из 50 билетов 8 выигрышных. Какова вероятность того, что среди пяти наугад выбранных билетов два окажутся выигрышными?
Из 60 экзаменационных вопросов учащийся подготовил 50. На экзамене он должен ответить на два вопроса. Какова вероятность того, что учащийся ответит на оба вопроса?
Из 10 билетов лотереи выигрышными являются два. Какова вероятность того, что среди взятых наудачу пяти билетов два выигрышных?
Из 50 электролампочек имеется 4 бракованных. Какова вероятность того, что две взятые наугад лампы окажутся бракованными?
Экзаменационные билеты занумерованы числами от 1 до 35. Какова вероятность того, что номер выбранного билета четный?
В партии из 100 деталей 5% бракованных. Какова вероятность того, что наугад выбранная деталь окажется стандартной?
В ящике 14 деталей, среди которых 8 окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что только 3 извлеченные детали окажутся окрашенными.
Задания программированной контрольной работы занумерованы всеми двухзначными числами. Какова вероятность того, что номер наугад выбранного задания состоит из одинаковых цифр?
Из шести одинаковых карточек разрезной азбуки: «а», «е», «м», «н», «о», «р» наудачу выбирают четыре карточки и складывают их в ряд в порядке их извлечения. Какова вероятность получить при этом слово «море»?
Четырехтомное собрание сочинений Н.В.Гоголя расположено на полке в случайном порядке. Какова вероятность того, что а) тома стоят по порядку номеров; б) хотя бы один том не стоит на своем месте?
11). В отделе работают 7 мужчин и 3 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них две женщины.
12). Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в подкомитете будут менеджеры.
13). На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, нет изготовленных в Симферополе.
14). В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных - две квитанции заполнены неверно.
15). В группе 13 студентов, среди которых 5 отличников. По списку наудачу отобраны 8 студентов. Найти вероятность того, что среди них трое отличников.
16). В компьютерном классе 10 машин, 7 из которых подключены к сети Internet. Наудачу выбраны три машины. Найти вероятность того, что одна из них подключена к сети Internet.
17). В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных только одна бракованная.
18). В чемпионате института по футболу участвуют 6 команд, 4 из которых представляют факультет экономики. Для жеребьевки декан пригласил трех капитанов команд, какова вероятность того, что все они с факультета экономики?
19). Из 30 вопросов, входящих в билеты зачета студент подготовил 26. Какова вероятность того, что взятый наудачу студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?
20). В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных нет неверно заполненных квитанций.
Задачи № 21-40. Используя теоремы сложения и умножения вероятностей, решить задачу:
21) Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только два устройства б) хотя бы одно.
22) Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,75. Найти вероятность того, что среди трех проверенных изделий: а) только два изделия высшего сорта; б) хотя бы одно изделие высшего сорта.
23) Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.
24) Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем ящике соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что деталь содержится: а) не более чем в двух ящиках; б) хотя бы в одном ящике.
25) Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятности того, что при однократном измерении: а) хотя бы один из исследователей допустит ошибку; б) только один исследователь допустит ошибку.
26) Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попал в цель; б) хотя бы два стрелка попали в цель.
27) Вероятности того, что нужная формула имеется в первом, втором, третьем справочнике соответственно равны 0,9; 0,6; 0,7. Найти вероятности того, что формула содержится: а) во всех трех справочниках; б) хотя бы в одном справочнике.
28) Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,8, вторым – 0,7, третьим – 0,6. Найти вероятность того, что: а) только два попали в цель; б) хотя бы один стрелок попал в цель.
29). В мешке смешаны нити, среди которых 80% белые, а остальные - красные. Определить вероятность того, что вынутые наудачу две нити окажутся: а) одного цвета; б) разных цветов.
30). Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок равна 0.3, второй - 0.35, третий - 0.15. Найти вероятность того, что в течение смены внимания рабочего потребуют: а) какие-либо два станка; б) хотя бы один станок.
31). В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров: а) нет синих; б) нет красных.
32). Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0.85. Найти вероятность того, что из трех проверенных деталей: а) только две будут стандартные; б) хотя бы одна стандартная.
33). Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство равна 0.7, второе - 0.9. Найти вероятность того, что при аварии сработает: а) только одно устройство; б). Хотя бы одно устройство.
34). В одном ящике 3 белых и 7 красных шаров, в другом 6 белых и 4 красных. Из каждого ящика наудачу извлекают по одному шару. Найти вероятность того, что оба извлеченных шара: а) красные; б) хотя бы один белый.
35). Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство равна 0.7, второе - 0.9. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) хотя бы одно устройство.
36). Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем ящике соответственно равны 0.7, 0.5, 0.9. Найти вероятность того, что деталь содержится: а) только в двух ящиках; б) хотя бы в одном ящике.
37). Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок равна 0.3, второй - 0.35, третий -0.15. Найти вероятность того, что в течение смены внимания рабочего потребует: а) только два станка; б) хотя бы один станок.
38). Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0.85. Найти вероятность того, что из трех проверенных деталей: а) только две нестандартные; б) хотя бы одна нестандартная.
39). Студент записан в три библиотеки, в которых он разыскивает нужную ему книгу по комбинаторике. Вероятность найти книгу в первой библиотеке равна 0.2, во второй - 0.7, в третьей - 0.5. Найти вероятность того, что книгу можно найти: а) хотя бы в одной библиотеке; б). только в двух библиотеках.
40). В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров нет белых шаров?
Задачи № 41-60. Используя формулу полной вероятности и формулу Бейеса, решить задачу:
41) Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,04, в период экономического кризиса – 0,13. Предположим, что вероятность того, что начнется период экономического роста, равна 0,65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?
42) При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0,65, если председатель совета директоров поглащаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха равна 0,3. Предполагается, что вероятность ухода в отставку председателя составляет 0,7. Чему равна вероятность успеха сделки?
43) Агент по недвижимости пытается продать участок земли под застройку. Он полагает, что участок будет продан в течение ближайших шести месяцев с вероятностью 0,9 (если экономическая ситуация в регионе не будет ухудшаться). Если же экономическая ситуация будет ухудшаться, то вероятность продать участок уменьшится до 0,5. Экономист, консультирующий агента, полагает, что с вероятностью, равной 0,7 экономическая ситуация в регионе в течение следующих шести месяцев будет ухудшаться. Чему равна вероятность того, что участок будет продан в течение ближайших шести месяцев?
44) Три организации представили в контрольное управление счета для выборочной проверки: первая – 10 счетов, вторая – 20, третья – 15. Вероятности правильного оформления счетов у этих организаций соответственно равны: 0,95; 0,8; 0,9. Какова вероятность того, что выбранный счет правильный? Определить вероятность того, что этот счет принадлежит третьей организации.
45) Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны).
46) Судоходная компания организует средиземноморские круизы в течение летнего времени и проводит несколько круизов в сезон. Поскольку в этом виде бизнеса очень высокая конкуренция, то важно, чтобы все каюты зафрахтованного под круизы корабля были полностью заняты туристами, тогда компания получит прибыль. Эксперт по туризму, нанятый компанией, предсказывает, что вероятность того, что корабль будет полон в течение сезона, равна 0,92, если доллар не подорожает по отношению к рублю, и с вероятностью 0,75, если доллар подорожает. По оценкам экономистов, вероятность того, что в течение сезона доллар подорожает по отношению к рублю, равна 0,23. Чему равна вероятность того, что билеты на все круизы будут проданы?
47) Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,1, в период экономического кризиса – 0,25. Предположим, что вероятность того, что начнется период экономического роста, равна 0,7. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?
48) При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0,7, если председатель совета директоров поглащаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха равна 0,4. Предполагается, что вероятность ухода в отставку председателя составляет 0,8. Чему равна вероятность успеха сделки?
49) Ткань проходит через 4 машины. Вероятность появления брака на первой машине равна 0,12; на второй – 0,1; на третьей – 0,15; на четвертой – 0,07. В конце ткани обнаружен брак. Какова вероятность того, что этот брак дала вторая машина?
50) Три организации представили в контрольное управление счета для выборочной проверки: первая – 20 счетов, вторая – 10, третья – 30. Вероятности правильного оформления счетов у этих организаций соответственно равны: 0,8; 0,9; 0,7. Какова вероятность того, что выбранный счет правильный? Определить вероятность того, что этот счет принадлежит второй организации.
51). В студенческой группе 20 человек. из них 4 человека сдали экзамен по высшей математике на «отлично», 11 на «хорошо» и 5 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0.9, для хорошиста 0.8, для троечника 0.7. Определить вероятность того, что наудачу выбранный студент не решит задачу.
52). В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0.9, для велосипедиста 0.8 и для бегуна 0.75. Найти вероятность того, что наудачу выбранный спортсмен не выполнит норму.
53). Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 4 студента, из второй группы 6 студентов, из третьей группы 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0.6, 0.9, 0.5. Найти вероятность того, что наудачу выбранный студент не попадет в сборную.
54). Имеется два одинаковых ящика с шарами. В первом ящике 4 белых и 6 красных шаров, во втором 5 белых и 10 красных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется белым?
55). Предприятие имеет три источника поставки комплектующих - фирмы А, В, С. на долю фирмы А приходится 50% общего объема поставок, В - 30% и С - 20%. Из практики известно, что 10% поставляемых фирмой А деталей - бракованные, В - 5% и С - 6%. Какова вероятность того, что наугад взятая деталь стандартная?
56). В первом ящике 20 деталей, из них 15 стандартные. Во втором ящике 25 деталей, из них 20 стандартные. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика - стандартная.
57). В первой урне 3 белых и 7 черных шаров, во второй - 6 белых и 4 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Какова вероятность того, что вынутый шар ранее находился во второй урне, если известно, что он белый.
58). Сборщик получил 5 коробок деталей изготовленных заводом №1 и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна равна 0.9, а завода №2 - 0.72. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
59). В студенческой группе 25 человек. из них 5 человека сдали экзамен по высшей математике на «отлично», 12 на «хорошо» и 8 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0.9, для хорошиста 0.8, для троечника 0.7. Определить вероятность того, что наудачу выбранный студент решит задачу.
60). На заводе изготовляют комплектующие детали. Первая машина производит 25% всех изделий, вторая 35%, третья 40%. Брак составляет соответственно 5%, 4% и 10%. Какова вероятность того, что случайно выбранная деталь имеет дефект?
Задание 61-80. Повторные независимые испытания по схеме Бернулли
61). Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 600 взятых наугад изделий: а) 25 бракованных; б) бракованных менее 25 изделий.
62). Вероятность события А в каждом испытании равна 0.2. Произведено 400 испытания. Найти вероятность того, что событие А наступит: а) ровно 75 раз; б) менее 75 раз.
63). В первые классы должно быть принято 200 детей. Вероятность рождения мальчика равна 0.515.Определить вероятность того, что среди них окажется: а) не более 100 мальчиков; б) 100 девочек.
64). Вероятность появления успеха в каждом испытании равна 0.4. Найти вероятность того, что при 550 испытаниях успех наступит: а) ровно 200 раз; б) не менее 210 и не более 240 раз.
65). Вероятность появления успеха в каждом испытании равна 0.3. Найти вероятность того, что при 400 испытаниях успех наступит: а) не более 110 раз; б) ровно 110 раз.
66). В первые классы должно быть принято 400 детей. Вероятность рождения мальчика равна 0.515. Определить вероятность того, что среди них окажется: а) не менее 200 девочек; б) 200 девочек.
67). Вероятность рождения мальчика равна 0.515, а девочки - 0.485. в некоторой семье шестеро детей. Найти вероятность того, что среди них: а) все мальчики; б) не больше двух девочек.
68). Вероятность появления события А равна 0.6. Какова вероятность того, что при 800 испытаниях событие А появится: а). ровно 470 раз; б) не более 470 раз?
69). Вероятность поражения мишени при одном выстреле равна 0.8. Найти вероятность того, что при 300 выстрелах мишень будет поражена: а) ровно 230 раз; б) не менее 230 раз.
70). Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 500 взятых наугад изделий: а) 20 бракованных; б) бракованных менее 20 изделий.
71). Вероятность события А в каждом испытании равна 0.2. Произведено 400 испытания. Найти вероятность того, что событие А наступит: ровно 90 раз; б) не менее 75 и не более 90 раз
72). Вероятность поражения мишени при одном выстреле равна 0.9. Найти вероятность того, что при 200 выстрелах мишень будет поражена: а) не менее 175 раз; б) ровно 175 раз.
73). Вероятность изготовления нестандартной детали на станке-автомате равна 0.003. Найти вероятность того, что среди 1000 деталей окажется: а). не менее 3 нестандартных; б). 4 нестандартных.
74). Принимая вероятность рождения девочки равной 0,5 , найти вероятность того, что из 800 родившихся детей девочек: а) будет 420; б) не менее 400.
75). Вероятность появления события в каждом из независимых испытаний равна 0,7. Найти вероятность того, что в 900 испытаниях событие произойдет: а) не менее 600 и не более 850 раз; б) ровно 660 раз.
76). Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что в 100 испытаниях событие наступит: а) более 35 раз; б) 20 раз.
77). Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей бракованных окажется: а) ровно 3; б) не более трех.
78). Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,9. Найти вероятность тог, что при 100 выстрелах стрелок поразит мишень: а) ровно 50 раз; б) не менее 80 и не более 95 раз
79). Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 20 и не более 60 раз; б) 80 раз.
80). Вероятность появления события в каждом из независимых испытаний равна 0,4. Найти вероятность того, что в серии из 1500 испытаний это событие произойдет: а) не менее 800 и не более 1100 раз; б) 600 раз.
Задачи № 81-100. Дискретные случайные величины.
Независимые дискретные величины X и Y заданы законами распределения: Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z .
81.
| X | -6 | 8 | 9 | 10 | Y | -8 | 2 | ||
| p | 0,1 | 0,1 | 0,6 | 0,2 | p | 0,4 | 0,6 |
Z=3X-2Y
82.
| X | -2 | -1 | 0 | 3 | Y | -3 | 2 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=3X-2Y.
83.
| X | -6 | 8 | 9 | 10 | Y | -8 | 2 | |
| p | 0,1 | 0,1 | 0,6 | 0,2 | p | 0,4 | 0,6 |
Z=3X-Y.
84.
| X | -5 | -4 | 2 | 3 | Y | -8 | -1 | |
| p | 0,1 | 0,5 | 0,2 | 0,2 | p | 0,7 | 0,3 |
Z=3X-2Y.
85.
| X | -6 | -3 | 2 | 1 | Y | -2 | 8 | |
| p | 0,3 | 0,3 | 0,2 | 0,2 | p | 0,2 | 0,8 |
Z=3X-2Y.
86.
| X | -6 | 8 | 9 | 10 | Y | -8 | 2 | |
| p | 0,1 | 0,1 | 0,6 | 0,2 | p | 0,4 | 0,6 |
Z=2X+4Y.
87.
| X | -5 | -4 | 2 | 3 | Y | -8 | -1 | |
| p | 0,1 | 0,5 | 0,2 | 0,2 | p | 0,7 | 0,3 |
Z=3X-Y.
88.
| X | -6 | -3 | 2 | 1 | Y | -2 | 8 | |
| p | 0,3 | 0,3 | 0,2 | 0,2 | p | 0,2 | 0,8 |
Z=2X+4Y.
89.
| X | -4 | -2 | -1 | 3 | Y | -3 | -1 | |
| p | 0,1 | 0,3 | 0,2 | 0,4 | p | 0,4 | 0,6 |
Z=3X-2Y.
90.
| X | -5 | -4 | 2 | 3 | Y | -8 | -1 | |
| p | 0,1 | 0,5 | 0,2 | 0,2 | p | 0,7 | 0,3 |
Z=2X+4Y.
91.
| X | -2 | -1 | 0 | 3 | Y | -3 | 2 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=2X+4Y.
92.
| X | -6 | -3 | 2 | 1 | Y | -2 | 8 | |
| p | 0,3 | 0,3 | 0,2 | 0,2 | p | 0,2 | 0,8 |
Z=3X-Y.
93.
| X | -4 | -2 | -1 | 3 | Y | -3 | -1 | |
| p | 0,1 | 0,3 | 0,2 | 0,4 | p | 0,4 | 0,6 |
Z=3X-Y.
94.
| X | -4 | -2 | -1 | 3 | Y | -3 | -1 | |
| p | 0,1 | 0,3 | 0,2 | 0,4 | p | 0,4 | 0,6 |
Z=2X+4Y.
95.
| X | -2 | -1 | 0 | 3 | Y | 1 | 2 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=2X-3Y.
96.
| X | -2 | -1 | 0 | 3 | Y | -3 | 2 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=3X-Y.
97.
| X | -2 | -1 | 0 | 3 | Y | -3 | 2 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=X-4Y.
98.
| X | -3 | -1 | 0 | 2 | Y | -2 | 2 | |
| p | 0,1 | 0,5 | 0,1 | 0,3 | p | 0,4 | 0,6 |
Z=3X-Y.
99.
| X | -1 | 0 | 1 | 2 | Y | 2 | 3 | |
| p | 0,2 | 0,5 | 0,1 | 0,2 | p | 0,3 | 0,7 |
Z=3X+Y.
100.
| X | -3 | -2 | 0 | 1 | Y | -4 | 3 | |
| p | 0,2 | 0,4 | 0,2 | 0,2 | p | 0,3 | 0,7 |
Z=2X-4Y.
Задачи №101-120. Непрерывные случайные величины.
Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X; б) вероятность попадания случайной величины в интервал (А;В); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X. Построить графики функции и плотности распределения случайной величины Х.
101. 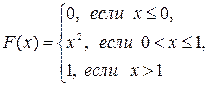 А=0,2; B=0,9.
А=0,2; B=0,9.
102. 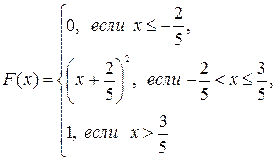 А=0; В=
А=0; В= 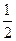 .
.
103. 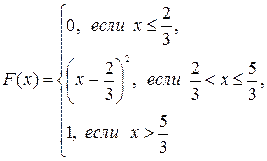 А=1; В=
А=1; В= 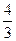 .
.
104. 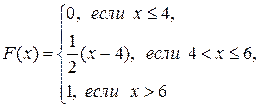 А=
А=  ; В= 5.
; В= 5.
105. 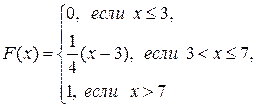 А=4; В= 5.
А=4; В= 5.
106. 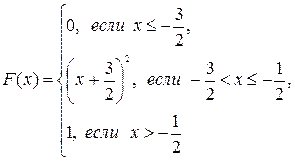 А=-1; В=
А=-1; В= 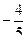 .
.
107. 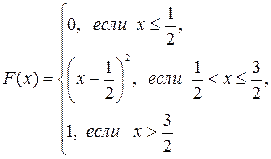 А=
А= 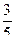 ; В=
; В=  .
.
108.  А=3; В=6.
А=3; В=6.
109.  А=-1; В=2.
А=-1; В=2.
110. 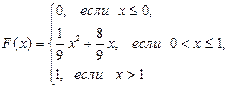 А=
А= 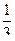 ; В=
; В=  .
.
111.  А=
А= 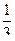 ; В=
; В=  .
.
112. 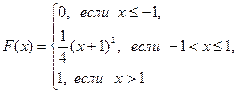 А=
А= 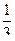 ; В=
; В=  .
.
113. 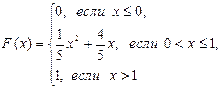 А=
А= 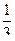 ; В=
; В=  .
.
114. 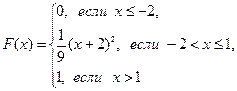 А=
А= 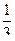 ; В=
; В=  .
.
115. 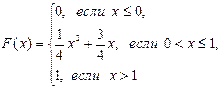 А=
А= 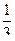 ; В=
; В=  .
.
116.  А=
А= 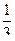 ; В=
; В=  .
.
117. 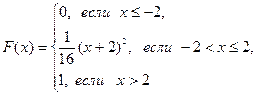 А=
А= 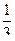 ; В=
; В=  .
.
118. 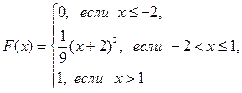 А=
А= 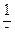 ; В=
; В=  .
.
119. 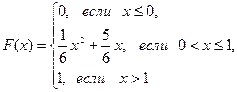 А=
А= 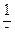 ; В=
; В=  .
.
120. 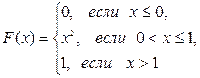 А=
А= 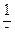 ; В=
; В= 
Дата: 2019-05-28, просмотров: 592.