Пусть эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частот.
1. Находим выборочную среднюю, дисперсию, среднеквадратическое отклонение. В качестве вариант принимают среднее арифметическое концов интервала.
2. Нормируют случайную величину 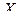 , то есть переходят к величине
, то есть переходят к величине 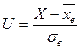 и находят значения
и находят значения 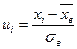 .
.
3. Находят значение функции Лапласа 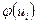 .
.
4.Вычисляют значение 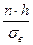 и умножают на
и умножают на 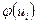 .
.
5. Получаем теоретические частоты 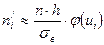 .
.
6. Сравниваем эмпирические и теоретические частоты. Для этого:
а) находим наблюдаемое значение критерия Пирсона:
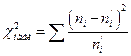 .
.
Эта величина случайная, так как в различных опытах она принимает различные заранее не известные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина 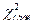 , то есть он характеризует близость эмпирического и теоретического распределения.
, то есть он характеризует близость эмпирического и теоретического распределения.
б) по таблице критических точек распределения 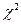 , по заданному уровню значимости
, по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы 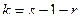 , где
, где 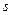 - число групп выборки;
- число групп выборки; 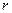 - это число параметров предполагаемого распределения, которые оценены по данным выборки. найдем критическую точку
- это число параметров предполагаемого распределения, которые оценены по данным выборки. найдем критическую точку 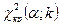 .
.
Если 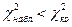 - нет оснований отвергать нулевую гипотезу.
- нет оснований отвергать нулевую гипотезу.
Если  - нулевую гипотезу отвергают.
- нулевую гипотезу отвергают.
Замечание. В частности, если предполагаемое распределение – нормальное  , то оценивают два параметра, математическое ожидание и среднее квадратическое отклонение, поэтому
, то оценивают два параметра, математическое ожидание и среднее квадратическое отклонение, поэтому 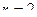 и число степеней свободы
и число степеней свободы 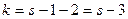 .
.
Пример: Дано следующее статистическое распределение выборки
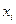
| 156 | 160 | 164 | 168 | 172 | 176 | 180 |
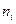
| 10 | 14 | 26 | 28 | 12 | 8 | 2 |
Найти теоретические частоты данного распределения и проверить гипотезу о нормальном законе этого распределения при уровне значимости 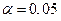 с помощью критерия согласия
с помощью критерия согласия 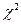 Пирсона.
Пирсона.
Решение:
Подсчитаем выборочную среднюю и среднеквадратическое отклонение.
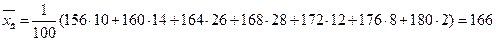

 и
и  .
.
Составим расчетную таблицу для вычисления теоретических частот пользуюсь указанной схемой. Для этого найдем величину 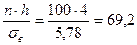 .(h-длина интервала или шаг).
.(h-длина интервала или шаг).
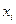
| 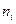
| 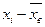
| 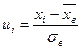
| 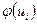
| 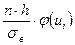
| 
|
| 156 | 10 | -10 | -1,73 | 0,0893 | 6,18 | 6 |
| 160 | 14 | -6 | -1,04 | 0,2323 | 16,08 | 16 |
| 164 | 26 | -2 | -0,35 | 0,3752 | 25,96 | 26 |
| 168 | 28 | 2 | 0,35 | 0,3752 | 25,96 | 26 |
| 172 | 12 | 6 | 1,04 | 0,2323 | 16,08 | 16,1 |
| 176 | 8 | 10 | 1,73 | 0,0893 | 6,18 | 6,2 |
| 180 | 2 | 14 | 2 | 0,054 | 3,73 | 3,7 |
| 100 | 100 |
Посчитаем величину
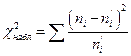 .
.
Воспользуемся расчетной таблицей
| 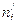
| 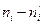
| 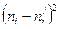
| 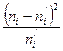
|
| 10 | 6 | 4 | 16 | 2,67 |
| 14 | 16 | -2 | 4 | 0,25 |
| 26 | 26 | 0 | 0 | 0 |
| 28 | 26 | 2 | 4 | 0,15 |
| 12 | 16,1 | -4,1 | 16,81 | 1,04 |
| 8 | 6,2 | 1,8 | 3,24 | 0,52 |
| 2 | 3,7 | 1,7 | 2,89 | 0,78 |
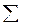
| 5,41 |
Таким образом, 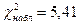 .
.
Найдем  . Так как
. Так как 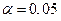 и
и 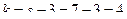 , то
, то  .
.
Так как 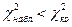 , то нет оснований отвергать гипотезу о нормальном законе распределения данной величины, то есть она принимается при уровне значимости
, то нет оснований отвергать гипотезу о нормальном законе распределения данной величины, то есть она принимается при уровне значимости 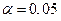 и есть основания считать, что эмпирические и теоретические частоты различаются не значимо, различия случайны.
и есть основания считать, что эмпирические и теоретические частоты различаются не значимо, различия случайны.
Пример решения типовой задачи
Комитетом по физической культуре и спорту были проведены исследования спортсменов, занимающихся стрельбой. Было отобрано 200 стрелков из 4000 для определения среднего количества патронов, необходимых одному спортсмену для одной тренировки. Результаты обследования приведены в таблице
| Число патронов (шт.) | Менее 200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | Более 700 |
| Число спортсменов (чел.) | 4 | 20 | 57 | 65 | 31 | 15 | 8 |
1. Перейти к вариационному ряду, и построить полигон частот.
2. Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.
4. Используя критерий 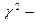 Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение.
1. Перейдем от данного интервального ряда к вариационному. Для этого найдем середину каждого интервала (сложим концы каждого интервала и поделим пополам):
| Число патронов (шт.), х i | 150 | 250 | 350 | 450 | 550 | 650 | 750 |
| Число спортсменов (чел.), ni | 4 | 20 | 57 | 65 | 31 | 15 | 8 |
Построим полигон частот для полученного вариационного ряда.
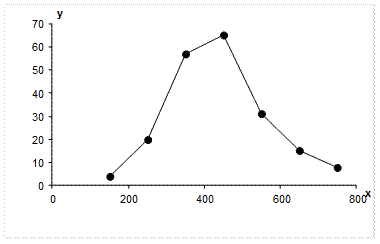
2. Находим выборочную среднюю по формуле:
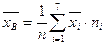 .
.
Объем выборки n=200.
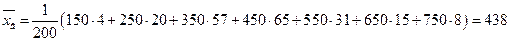
Таким образом, среднее число патронов необходимых одному спортсмену для одной тренировки равно 438 шт.
Находим выборочную дисперсию:
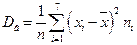 = 16656
= 16656
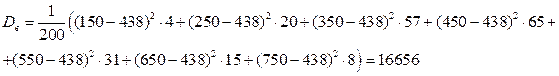
Посчитаем выборочную дисперсию вторым способом:
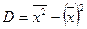 , где
, где 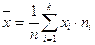 и
и 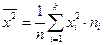 .
.
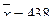
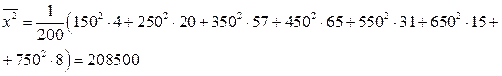
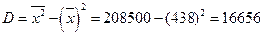
Среднеквадратическое отклонение: 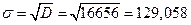
Исправленную выборочную дисперсию посчитаем по формуле:
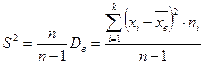
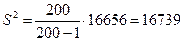
Исправленное выборочное среднеквадратическое отклонение случайной величины Х :
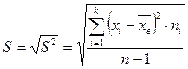

3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95. Тем самым, найдем границы, в которых с вероятностью 0,95 заключено среднее число патронов, необходимых для тренировки одного спортсмена.
Доверительный интервал для генеральной средней находим по формуле:
 , где
, где 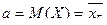 - математическое ожидание;
- математическое ожидание;
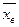 - выборочная средняя;
- выборочная средняя;
 - объем выборки;
- объем выборки;
 - при большом объеме выборки;
- при большом объеме выборки;
t- значение аргумента функции Лапласа, при котором она равна 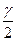 , то есть
, то есть 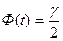 , где
, где 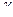 - заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95
- заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95 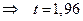 .
.

 ;
; 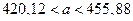
Доверительный интервал для оценки среднеквадратического отклонения  вычисляется по формуле
вычисляется по формуле
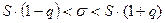 ,
,
где 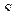 - это исправленное среднеквадратическое отклонение;
- это исправленное среднеквадратическое отклонение;
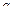 - это табличное значение, которое зависит от объема выборки
- это табличное значение, которое зависит от объема выборки  и заданной надежности
и заданной надежности 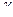 , то есть
, то есть 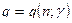 (приложение 4).
(приложение 4).
Найдем значение q: 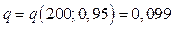
Тогда доверительный интервал для оценки среднеквадратического отклонения  будет равен:
будет равен:
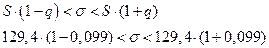
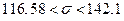
4. Используя критерий 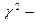 Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Примечание: В качестве дисперсии нормального закона распределения следует взять исправленную выборочную дисперсию. Но т.к. количество наблюдений – 200 достаточно велико, то подойдет и “обычная”  .
.
| xi | ni | 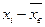
| 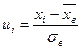
| 
| 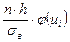
| 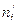
|
| 150 | 4 | -288 | -2,23 | 0,0332 | 5,144974 | 5,1 |
| 250 | 20 | -188 | -1,46 | 0,1374 | 21,29275 | 21,3 |
| 350 | 57 | -88 | -0,68 | 0,3166 | 49,06321 | 49,1 |
| 450 | 65 | 12 | 0,09 | 0,3973 | 61,56922 | 61,6 |
| 550 | 31 | 112 | 0,87 | 0,2732 | 42,33755 | 42,3 |
| 650 | 15 | 212 | 1,64 | 0,1040 | 16,11678 | 16,1 |
| 750 | 8 | 312 | 2,42 | 0,0213 | 3,300841 | 3,3 |
| 200 | 198,8 |
Составим расчетную таблицу для вычисления теоретических частот пользуюсь указанной схемой.
Для этого найдем величину
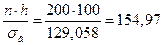 .(h-длина интервала или шаг).
.(h-длина интервала или шаг).
Из первого пункта данной задачи известно, что 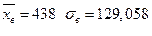 .
.
Составим таблицу для подсчета 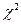
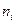
| 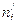
| 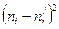
| 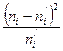
|
| 4 | 5,1 | 1,21 | 0,237255 |
| 20 | 21,3 | 1,69 | 0,079343 |
| 57 | 49,1 | 62,41 | 1,271079 |
| 65 | 61,6 | 11,56 | 0,187662 |
| 31 | 42,3 | 127,69 | 3,018676 |
| 15 | 16,1 | 1,21 | 0,075155 |
| 8 | 3,3 | 22,09 | 6,693939 |
| 200 | 198,8 | 11,56311 |
Итого, значение статистики  .
.
Определим количество степеней свободы по формуле: 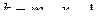 .
.
m–число интервалов (m=7), r – число параметров закона распределения (в нормальном распределении r = 2)
Т.е. k = 7-2-1=4.
Соответствующее критическое значение статистики 
Поскольку  , гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
, гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
Ниже показана кривая эмпирического (сплошная линия) и теоретического (пунктирная линия) распределений

Вывод. Сопоставив обе кривых видим, что наилучшее соответствие эмпирических данных нормальному распределению наблюдается на первом, втором, и шестом интервалах, что подтверждается таблицей. А вот на участке от 500 до 600 патронов отклонение очень большое – это видно из графика. Оно и оказало “фатальное” влияние на критерий согласия – это видно из таблицы.
Дата: 2019-05-28, просмотров: 460.