Корреляционное отношение удовлетворяет двойному неравенству
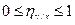 и
и  .
.
Если  и
и  , то признаки
, то признаки  и
и  не связаны между собой корреляционной зависимостью.
не связаны между собой корреляционной зависимостью.
Если корреляционное отношение 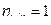 , то между признаками
, то между признаками  и
и  существует функциональная зависимость.
существует функциональная зависимость.
Выборочный коэффициент линейной корреляции  по абсолютной величине не больше корреляционных отношений, то есть
по абсолютной величине не больше корреляционных отношений, то есть
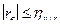 и
и 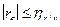 .
.
Если 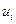 - это условные варианты признака
- это условные варианты признака 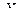 , и
, и  - это условные варианты признака
- это условные варианты признака  , то
, то
 и
и 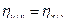 .
.
Как показывает первое свойство, корреляционное отношение может принимать значения из промежутка от 0 до 1, причем, чем ближе значение корреляционного отношения к 1, тем теснее связь между рассматриваемыми признаками, и чем ближе это значение к 0, тем слабее связь между рассматриваемыми признаками.
Замечание: Как было сказано выше, корреляционное отношение служит мерой тесноты любой связи, в том числе и линейной формы. В этом состоит преимущество корреляционного отношения. Но так же оно имеет и недостатки: а) оно определяют только тесноту связи, но не указывают на направление связи, так как они вычисляются с помощью средних квадратических отклонений, которые всегда положительны; б) оно не позволяет судить на сколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т.д. Это объясняется тем, что при определении корреляционного отношения форма связи во внимание не принимается.
Пример. Распределение признаков 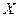 и
и  приведено в следующей корреляционной таблице
приведено в следующей корреляционной таблице
| X Y | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | ny |
| -2 | 1 | 2 | 1 | 4 | ||||||
| -1 | 1 | 3 | 3 | 1 | 8 | |||||
| 0 | 2 | 4 | 4 | 2 | 12 | |||||
| 1 | 1 | 5 | 5 | 1 | 12 | |||||
| 2 | 3 | 3 | 6 | |||||||
| nx | 4 | 7 | 5 | 4 | 2 | 4 | 5 | 7 | 4 | 42 |
Найти корреляционные отношения  и
и  , и сравнить их с соответствующим коэффициентом линейной корреляции.
, и сравнить их с соответствующим коэффициентом линейной корреляции.
Решение.
Найдем групповые средние:
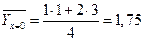 ;
; 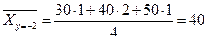 ;
;
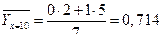 ;
;  ;
;
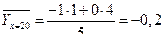 ;
;  ;
;
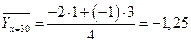 ;
; 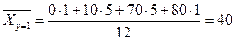 ;
;
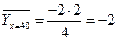 ;
;  .
.
 ;
;
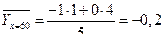 ;
;
 ;
;
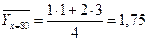 .
.
Для вычисления общих средних построим расчетные таблицы.
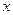
| 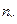
| 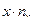
| 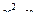
| 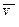
| 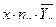
|
| 0 | 4 | 0 | 0 | 1,75 | 0 |
| 10 | 7 | 70 | 700 | 0,714 | 50 |
| 20 | 5 | 100 | 2000 | -0,2 | -20 |
| 30 | 4 | 120 | 3600 | -1,25 | -150 |
| 40 | 2 | 80 | 3200 | -2 | -160 |
| 50 | 4 | 200 | 10000 | -1,25 | -250 |
| 60 | 5 | 300 | 18000 | -0,2 | -60 |
| 70 | 7 | 490 | 34300 | 0,714 | 350 |
| 80 | 4 | 320 | 25600 | 1,75 | 560 |
| ∑ | 42 | 1680 | 97400 | - | 320 |

| 
| 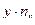
| 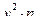
| 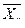
| 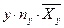
|
| -2 | 4 | -8 | 16 | 40 | -320 |
| -1 | 8 | -8 | 8 | 40 | -320 |
| 0 | 12 | 0 | 0 | 40 | 0 |
| 1 | 12 | 12 | 12 | 40 | 480 |
| 2 | 6 | 12 | 24 | 40 | 480 |
| ∑ | 42 | 8 | 60 | - | 320 |
Тогда:
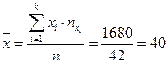 ;
;
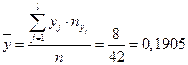 ;
;
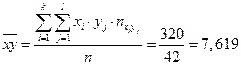 ;
;
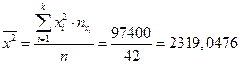 ;
;
 ;
;
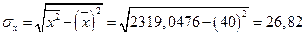 ;
;
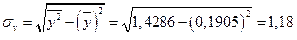 .
.
 , следовательно, линейной связи между признаками
, следовательно, линейной связи между признаками 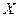 и
и  нет.
нет.
Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних 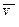 и
и 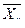 по формулам
по формулам
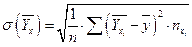 ,
, 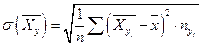 .
.
Получим
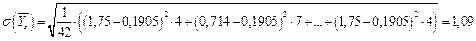 ;
;
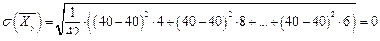 .
.
Тогда  ;
; 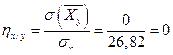 .
.
Корреляционное отношение 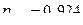 показывает, что признак
показывает, что признак  зависит от влияния признака
зависит от влияния признака 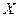 , а отношение
, а отношение  показывает, что признак
показывает, что признак 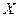 не зависит от влияния признака
не зависит от влияния признака  .
.
Пример решения типовой задачи
В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х (%) и стоимости Y (тыс. руб):
| Х \ У | 3-9 | 9-15 | 15-21 | 21-27 | 27-33 | Более 33 | итого |
| 20-30 | 2 | 5 | 2 | 9 | |||
| 30-40 | 4 | 8 | 4 | 3 | 19 | ||
| 40-50 | 4 | 10 | 20 | 10 | 44 | ||
| 50-60 | 5 | 36 | 23 | 6 | 70 | ||
| 60-70 | 12 | 11 | 11 | 34 | |||
| 70-80 | 6 | 10 | 16 | ||||
| 80-90 | 8 | 8 | |||||
| Итого | 14 | 27 | 55 | 54 | 35 | 15 | 200 |
Необходимо:
1. Вычислить условные средние 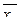 и
и 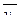 и построить эмпирические линии регрессии.
и построить эмпирические линии регрессии.
2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;
б) вычислить коэффициент корреляции на уровне значимости 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
Решение:
Найдем условные средние по формулам
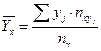 и
и 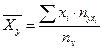 .
.
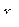 ,
, 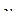 - середины соответствующих интервалов.
- середины соответствующих интервалов.
Найдем середины интервалов и запишем в таблицу:
| Х \ У | 6 | 12 | 18 | 24 | 30 | 36 | итого |
| 25 | 2 | 5 | 2 | 9 | |||
| 35 | 4 | 8 | 4 | 3 | 19 | ||
| 45 | 4 | 10 | 20 | 10 | 44 | ||
| 55 | 5 | 36 | 23 | 6 | 70 | ||
| 65 | 12 | 11 | 11 | 34 | |||
| 75 | 6 | 10 | 16 | ||||
| 85 | 8 | 8 | |||||
| Итого | 14 | 27 | 55 | 54 | 35 | 15 | 200 |
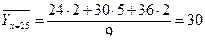


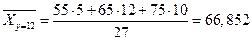


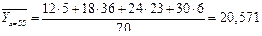
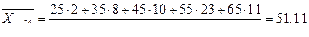


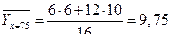

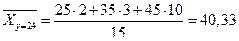
2а). Для нахождения уравнений регрессии вычисляем необходимые суммы. Для удобства их вычислений составим расчетные таблицы.
| 
| 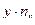
| 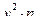
| 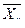
| 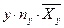
|
| 6 | 14 | 84 | 504 | 80,714 | 6778,8 |
| 12 | 27 | 324 | 3888 | 66,852 | 21675,6 |
| 18 | 55 | 990 | 17820 | 54,812 | 54261,9 |
| 24 | 54 | 1296 | 31104 | 51,11 | 66238,56 |
| 30 | 35 | 1050 | 31500 | 42,714 | 44847,6 |
| 36 | 15 | 540 | 19440 | 40,33 | 21778,2 |
| ∑ | 4284 | 104256 | - | 215580 |
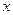
| 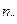
| 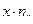
| 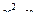
| 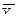
| 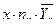
|
| 25 | 9 | 225 | 5625 | 30 | 6750 |
| 35 | 19 | 665 | 23275 | 25,895 | 17223,5 |
| 45 | 44 | 1980 | 89100 | 28,909 | 57239,82 |
| 55 | 70 | 3850 | 211750 | 20,571 | 79198,35 |
| 65 | 34 | 2210 | 143650 | 17,823 | 39388,83 |
| 75 | 16 | 1200 | 90000 | 9,75 | 11700 |
| 85 | 8 | 680 | 57800 | 6 | 4080 |
| ∑ | 10810 | 621200 | - | 215580 |

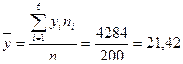
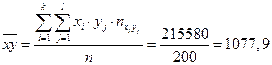


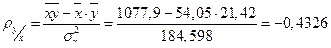
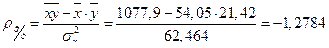
Тогда уравнение линейной регрессии у на х, будет иметь вид
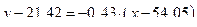 ,
,
или 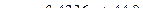
Тогда уравнение линейной регрессии х на у, будет иметь вид
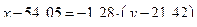 ,
,
или 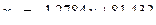
Ниже представлены графики полученных уравнений регрессии совместно с соответствующей эмпирической регрессией
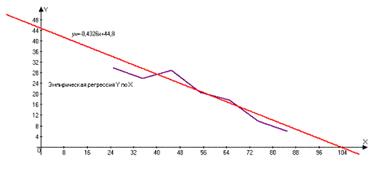

2б). Находим коэффициент корреляции 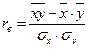
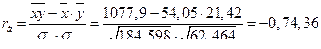
Так как 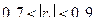 , то связь между рассматриваемыми признаками высокая, и так как
, то связь между рассматриваемыми признаками высокая, и так как  , то связь обратная.
, то связь обратная.
Проверим гипотезу о значимости коэффициента корреляции, то есть проверим гипотезу 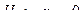 и
и
 .
.
Воспользуемся t - критерием Стьюдента, найдем 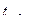 и
и 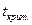 :
:
 .
.
Так как 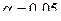 ,
, 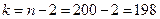 , то
, то
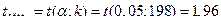 .
.
Таким образом, так как  , то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.
, то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.
2в). Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних 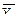 и
и 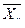 по формулам
по формулам
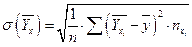 ,
,
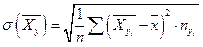 .
.
Получим
 ;
;
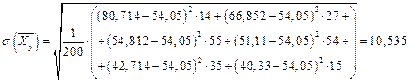 .
.
Тогда  ;
; 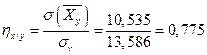 .
.
Корреляционное отношение 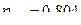 показывает, что признак
показывает, что признак  зависит от влияния признака
зависит от влияния признака 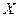 , а отношение
, а отношение 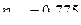 показывает, что признак
показывает, что признак 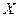 зависит от влияния признака
зависит от влияния признака  .
.
Дата: 2019-05-28, просмотров: 338.