Решение второй задачи корреляционного анализа, то есть определение тесноты связи между признаками, сводится к нахождению выборочного коэффициента линейной корреляции
 .
.
Значение коэффициента  изменяется в пределах от -1 до 1. Чем ближе значение
изменяется в пределах от -1 до 1. Чем ближе значение 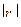 к 1, тем корреляционная связь между рассматриваемыми признаками теснее. Чем ближе значение
к 1, тем корреляционная связь между рассматриваемыми признаками теснее. Чем ближе значение 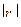 к нулю, тем слабее связь между рассматриваемыми признаками. Оценку тесноты линейной связи между можно представить в следующей таблице.
к нулю, тем слабее связь между рассматриваемыми признаками. Оценку тесноты линейной связи между можно представить в следующей таблице.
Оценка тесноты линейной связи
Значение 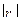
| 0-0,1 | 0,1-0,3 | 0,3- 0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 | 1 |
| Теснота линейной связи | Нет | Слабая | Умеренная | Заметная | Высокая | Очень высокая | Функциональная |
Знак коэффициента  указывает на направление связи. Если
указывает на направление связи. Если  , то связь между рассматриваемыми признаками прямая, то есть с увеличением значений одного признака значения другого признака тоже увеличиваются. Если
, то связь между рассматриваемыми признаками прямая, то есть с увеличением значений одного признака значения другого признака тоже увеличиваются. Если  , то связь между рассматриваемыми признаками обратная, то есть с увеличением значений одного признака значения другого признака уменьшаются.
, то связь между рассматриваемыми признаками обратная, то есть с увеличением значений одного признака значения другого признака уменьшаются.
Замечание: С помощью выборочного коэффициента корреляции можно судить не только о тесноте и направлении связи между признаками, но и предположить вид функциональной зависимости. Если значение 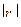 близко с корреляционным отношением
близко с корреляционным отношением  , то это дает основание выдвинуть гипотезу о том, что в генеральной совокупности функция регрессии линейная, то есть имеет вид
, то это дает основание выдвинуть гипотезу о том, что в генеральной совокупности функция регрессии линейная, то есть имеет вид 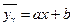 . Причем, заметим схожесть формулы для вычисления выборочного коэффициента корреляции и коэффициентов линейной регрессии
. Причем, заметим схожесть формулы для вычисления выборочного коэффициента корреляции и коэффициентов линейной регрессии  и
и 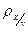 , запишем их
, запишем их
 ;
; 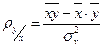 ;
; 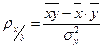 .
.
Следовательно, формулы для вычисления коэффициентов линейной регрессии можно преобразовать к виду
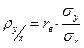 ;
;  .
.
Выборочный коэффициент корреляции  является оценкой для коэффициента корреляции
является оценкой для коэффициента корреляции 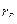 генеральной совокупности. Допустим, что выборочный коэффициент корреляции
генеральной совокупности. Допустим, что выборочный коэффициент корреляции  , найденный по выборке оказался отличен от нуля, то есть связь между рассматриваемыми признаками существует. Но это не значит, что коэффициент корреляции генеральной совокупности так же отличен от нуля, так как выборка производится случайным образом.
, найденный по выборке оказался отличен от нуля, то есть связь между рассматриваемыми признаками существует. Но это не значит, что коэффициент корреляции генеральной совокупности так же отличен от нуля, так как выборка производится случайным образом.
Поэтому, возникает необходимость проверки гипотезы о значимости коэффициента корреляции, то есть, значимо ли он отличается от нуля в генеральной совокупности.
Пусть  и
и 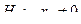 .
.
Если нулевая гипотеза будет принята, то коэффициент корреляции является не значимым, то есть он не значимо отличается от нуля в генеральной совокупности, следовательно, связь между рассматриваемыми признаками отсутствует. Если основная гипотеза будет отвергнута, то коэффициент корреляции является значимым, следовательно, связь между рассматриваемыми признаками существует.
Проверка гипотезы о значимости коэффициента корреляции производится по t- критерию Стьюдента. Для его применения необходимо знать две величины  и
и 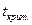 , которые сравнивают между собой, и, если будет получено неравенство
, которые сравнивают между собой, и, если будет получено неравенство  , то основную гипотезу отвергают и считают коэффициент корреляции значимым с вероятностью
, то основную гипотезу отвергают и считают коэффициент корреляции значимым с вероятностью 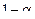 . В противном случае основную гипотезу принимают и считают коэффициент корреляции не значимым.
. В противном случае основную гипотезу принимают и считают коэффициент корреляции не значимым.
Наблюдаемое значение критерия  вычисляют по формуле
вычисляют по формуле

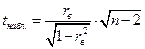 .
.
Для нахождения критического значения 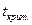 , необходимо знать уровень значимости
, необходимо знать уровень значимости  и число степеней свободы
и число степеней свободы 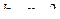 , и воспользоваться таблицей критических точек распределения Стьюдента (приложение 6).
, и воспользоваться таблицей критических точек распределения Стьюдента (приложение 6).
Кроме проверки гипотезы о значимости генерального коэффициента корреляции, находят для него доверительный интервал по формуле
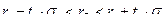 ,
,
где 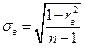 - это стандартная ошибка при вычислении выборочного коэффициента корреляции;
- это стандартная ошибка при вычислении выборочного коэффициента корреляции;
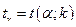 - табличное значение (приложение 6).
- табличное значение (приложение 6).
Пример. Найти выборочный коэффициент корреляции по данным, приведенным в таблице. Проверить значимость коэффициента корреляции при уровне значимости 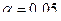 . Найти доверительный интервал для генерального коэффициента корреляции.
. Найти доверительный интервал для генерального коэффициента корреляции.
| x y | 2 | 3 | 5 | ny |
| 25 | 20 | 20 | ||
| 45 | 30 | 1 | 31 | |
| 110 | 1 | 48 | 49 | |
| nx | 20 | 31 | 49 | 100 |
Решение. Найдем условные средние
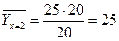 ;
; 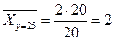 ;
;
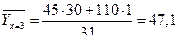 ;
; 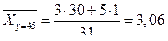 ;
;
 ;
; 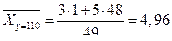 .
.
Для удобства вычислений составим расчетные таблицы.
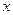
| 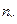
| 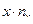
| 
| 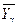
| 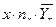
|
| 2 | 20 | 40 | 80 | 25 | 1000 |
| 3 | 31 | 93 | 279 | 47,1 | 4380,3 |
| 5 | 49 | 245 | 1225 | 108,67 | 26624,15 |
| ∑ | 100 | 378 | 1584 | - | 32004,45 |

| 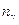
| 
| 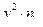
| 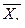
| 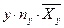
|
| 25 | 20 | 500 | 12500 | 2 | 1000 |
| 45 | 31 | 1395 | 62775 | 3,06 | 4268,7 |
| 110 | 49 | 5390 | 592900 | 4,96 | 26734,4 |
| ∑ | 100 | 7285 | 668175 | - | 32003,1 |
Тогда 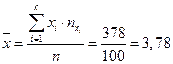 ;
; 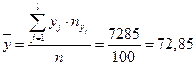 ;
;
 ;
; 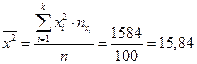 ;
;
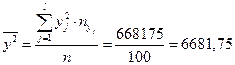 ;
;
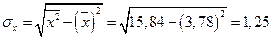 ;
;
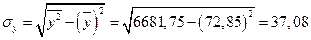 .
.
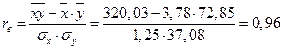 .
.
Так как 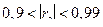 , то связь между рассматриваемыми признаками очень высокая, и так как
, то связь между рассматриваемыми признаками очень высокая, и так как  , то связь прямая.
, то связь прямая.
Проверим гипотезу о значимости коэффициента корреляции, то есть проверим гипотезу  и
и
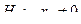 .
.
Воспользуемся t - критерием Стьюдента, найдем 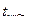 и
и 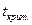 :
:
 .
.
Так как 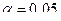 ,
, 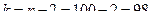 , то
, то
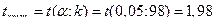 .
.
Таким образом, так как  , то основную гипотезу отвергаем и считаем генеральный коэффициент корреляции значимым с вероятностью 0,95, то есть он значимо отличается от нуля и связь между рассматриваемыми признаками X и Y в генеральной совокупности существует.
, то основную гипотезу отвергаем и считаем генеральный коэффициент корреляции значимым с вероятностью 0,95, то есть он значимо отличается от нуля и связь между рассматриваемыми признаками X и Y в генеральной совокупности существует.
Найдем доверительный интервал для генерального коэффициента корреляции, для этого рассчитаем стандартную ошибку для выборочного коэффициента корреляции 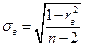 . Получим
. Получим
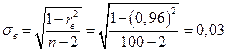 .
.
Найдем 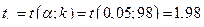 . Тогда доверительный интервал
. Тогда доверительный интервал 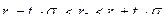 будет иметь вид:
будет иметь вид:
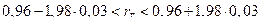 ;
;  .
.
Найденный интервал показывает, что при повторении опыта 100 раз в 95 случаях истинное значение коэффициента линейной корреляции генеральной совокупности будет заключено в интервале от 0,9 до 1.
Оценка тесноты любой связи
Как рассматривалось выше, оценка тесноты линейной связи осуществляется с помощью выборочного коэффициента корреляции. Но связь между признаками  и
и  не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
Пусть данные наблюдений над количественными признаками  и
и  сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения
сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения  , которые соответствуют определенному значению
, которые соответствуют определенному значению  .
.
Пример. Пусть дана следующая корреляционная таблица
| x y | 2 | 3 | 5 | ny |
| 25 | 20 | 20 | ||
| 45 | 30 | 1 | 31 | |
| 110 | 1 | 48 | 49 | |
| nx | 20 | 31 | 49 | 100 |
Данные этой таблиц можно разбить на группы относительно признаков  и
и  . Рассмотрим группы по признаку
. Рассмотрим группы по признаку  .
.
К первой группе относится 20 значений 
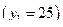 , которые соответствуют
, которые соответствуют 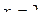 .
.
Ко второй группе относится 31 значений 
 , которые соответствуют
, которые соответствуют  .
.
К третей группе относится 49 значений 
 , которые соответствуют
, которые соответствуют 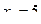 .
.
Таким образом, в данном случае, все исходные значения по признаку  , можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
, можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
 ;
; 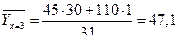 ;
;  .
.
Аналогично, можно разбить данные по признаку 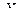 так же на три группы и найти групповые средние
так же на три группы и найти групповые средние 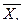 , получим
, получим
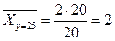 ;
; 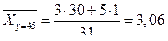 ;
; 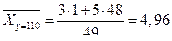 .
.
После разбиения данных на группы и вычисления групповых средних можно вычислить средние квадратические отклонения условных средних 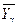 и
и 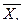 по формулам
по формулам 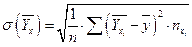 ,
, 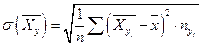 .
.
С помощью этих средних квадратических отклонений, вычисляют корреляционные отношения  по
по 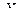 и
и  по
по  , по формулам
, по формулам
 и
и 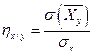 ,
,
где 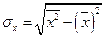 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака  ;
;
 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака  .
.
По приведенным корреляционным отношениям определяют тесноту любой связи, как линейной, так и нелинейной.
Дата: 2019-05-28, просмотров: 337.