Глава 10. Элементы корреляционного анализа
Основные понятия корреляционного анализа.
Во многих задачах требуется установить зависимость изучаемой случайной величины  от одной или нескольких случайных величин. Рассмотрим зависимость случайной величины
от одной или нескольких случайных величин. Рассмотрим зависимость случайной величины  от одной случайной (или неслучайной) величины
от одной случайной (или неслучайной) величины  .
.
Две случайные величины могут быть связаны между собой либо функциональной зависимостью, либо статистической, либо быть независимыми.
Определение . Функциональной называют зависимость, при которой каждому возможному значению случайной величины 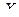 соответствует одно возможное значение случайной величины
соответствует одно возможное значение случайной величины  и обозначают
и обозначают
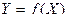 .
.
Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще воздействию случайных факторов, причем среди них могут быть и общие для обеих случайных величин факторы. Такую зависимость называют статистической.
Определение . Статистической называется зависимость, при которой изменение одной случайной величины влечет изменение закона распределения другой случайной величины.
Определение . Статистическая зависимость называется корреляционной, если при изменении одной случайной величины изменяется среднее значение другой.
Пример. Пусть случайная величина  - это количество внесенных удобрений, а
- это количество внесенных удобрений, а  - это урожайность зерна. Как показывает практика, между этими величинами нет функциональной связи, так как урожайность может зависеть и от других факторов (осадки, температура воздуха и др.), поэтому, от количества внесенных удобрений зависит только средняя урожайность, следовательно связь между случайными величинами
- это урожайность зерна. Как показывает практика, между этими величинами нет функциональной связи, так как урожайность может зависеть и от других факторов (осадки, температура воздуха и др.), поэтому, от количества внесенных удобрений зависит только средняя урожайность, следовательно связь между случайными величинами 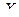 и
и  является корреляционной.
является корреляционной.
Таким образом, в основе корреляционного анализа лежит соотношение, существующее между значением одной случайной величины и средним значением другой.
Задача установления корреляционной связи распадается на две задачи. Первая состоит в установлении формы связи, то есть в определении вида функции, связывающей значения одной случайной величины со средним значением другой. Вторая задача состоит в оценке силы (тесноты) корреляционной связи. Рассмотрим каждую из этих задач.
10.2. Корреляционная таблица и корреляционное поле
Для установления формы связи между случайными величинами 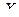 и
и  строят корреляционную таблицу, а затем корреляционное поле.
строят корреляционную таблицу, а затем корреляционное поле.
Пусть при выборе объема 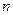 некоторое значение
некоторое значение 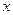 встречалось
встречалось 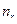 раз, некоторое значение
раз, некоторое значение 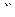 встречалось
встречалось  раз, и одна и та же пара чисел пара чисел
раз, и одна и та же пара чисел пара чисел 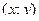 встречалась
встречалась 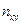 раз. Полученные данные удобно группировать в виде таблицы, которую называют корреляционной таблицей.
раз. Полученные данные удобно группировать в виде таблицы, которую называют корреляционной таблицей.
Поясним устройство корреляционной таблицы на примере.
Пример. Пусть  - это прибыль предприятия в год (млн. руб.);
- это прибыль предприятия в год (млн. руб.); 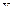 - это фонд материального поощрения (% от прибыли).
- это фонд материального поощрения (% от прибыли).
| x y | 10 | 20 | 30 | 40 | ny |
| 5 | 5 | 7 | 14 | 26 | |
| 10 | 2 | 6 | 4 | 12 | |
| 15 | 3 | 19 | 22 | ||
| nx | 8 | 21 | 13 | 18 | 60 |
В первой строке таблицы указаны наблюдаемые значения прибыли предприятия, а в первом столбце – процент от прибыли в фонд материального поощрения работников. На пересечении строк и столбцов находятся частоты  наблюдаемых пар значений
наблюдаемых пар значений 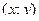 , например, пара (10;5) – встречалась на 5-ти предприятиях, а пара (30;15) – не встречалась не одного раза.
, например, пара (10;5) – встречалась на 5-ти предприятиях, а пара (30;15) – не встречалась не одного раза.
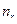 - это частота повторений значений
- это частота повторений значений 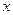 признака
признака 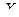 , равная сумме всех частот столбца, и указывающая, сколько раз всего встречалось данное значение
, равная сумме всех частот столбца, и указывающая, сколько раз всего встречалось данное значение 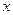 , например,
, например, 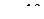 встречалось 8 раз.
встречалось 8 раз.
 - частота повторений значений
- частота повторений значений 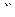 признака
признака 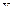 , равная сумме всех частот по строке и указывающая, сколько раз встречалось значение
, равная сумме всех частот по строке и указывающая, сколько раз встречалось значение 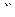 , например, значение
, например, значение 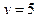 встречалось 26 раз.
встречалось 26 раз.
В правом нижнем углу таблицы указывается объем выборки 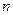 , равный сумме всех частот по строке (и по столбцу), то есть
, равный сумме всех частот по строке (и по столбцу), то есть
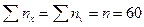 .
.
Таким образом выборка проведена по 60-ти предприятиям.
После того, как данные сгруппированы в виде корреляционной таблицы, строят корреляционное поле. Для этого в прямоугольной системе координат отмечают точки с координатами 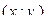 , то есть пары наблюдаемых значений величин
, то есть пары наблюдаемых значений величин  и
и  . По разбросу точек предполагают, какой именно можно считать связь между признаками, то есть с помощью какой функции ее можно описать.
. По разбросу точек предполагают, какой именно можно считать связь между признаками, то есть с помощью какой функции ее можно описать.
Пример. Построим корреляционное поле для предыдущего примера.
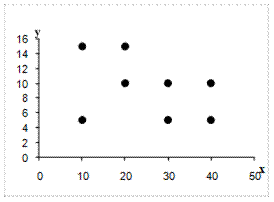
В данном примере связь предположительно можно считать линейной, так как все точки корреляционного поля располагаются в близи некоторой прямой линии.
Дата: 2019-05-28, просмотров: 362.