Для проверки нулевой гипотезы используют специально подобранную случайную величину, распределение которой известно. Обозначим эту величину .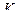

Определение . Статистическим критерием называют случайную величину , которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Определение . Наблюдаемым значением 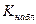 называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.

Определение . Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают, а совокупность значений критерия, при которых гипотезу принимают, называют областью принятия гипотезы.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают, а если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Критическая область и область принятия гипотезы, это есть некоторые интервалы, следовательно, существуют точки, которые их разделяют.

Определение . Критическими точками (границами)  называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством 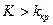, где 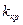- положительное число.

Левосторонней называют критическую область, определяемую неравенством , где - отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами 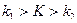, где .

В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствам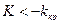и  и 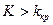 или равносильным неравенством .

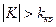Для отыскания правосторонней или левосторонней критической области, необходимо найти критическую точку 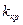. Для ее нахождения задаются достаточно малой вероятностью- уровнем значимости . Затем находят критическую точку 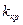, исходя из требований

 (для правосторонней области)

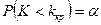 (для левосторонней области.).

Двусторонняя критическая область определяется неравенствами 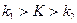. Поэтому, критические точки находят исходя из требований

.

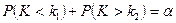Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этим требованиям.

После того, как критическая точка найдена, вычисляют по данным выборок наблюдаемое значение критерия 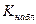, и если выполняется неравенство 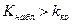, то нулевую гипотезу отвергают; если же 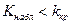, то нет оснований, чтобы отвергнуть нулевую гипотезу.

Наряду с уровнем значимости , то есть вероятностью того, что будет отвергнута правильная гипотеза, рассматривают вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза. Эту вероятность называют мощностью критерия.