1. Выборочное среднее равно 19,9. Гипотеза H0 для математического ожидания М
1). 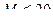 ; 2).
; 2).  ; 3).
; 3). 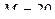 ; 4).
; 4). 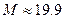 ; 5).
; 5). 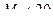 .
.
2. Относительная частота равна 0,25. Интервальная оценка вероятности может иметь вид:
1). (0; 1); 2). (0; 0,5); 3). (0,25; 0,5).
3. Статистическим аналогом математического ожидания является:
1). Абсолютная частота события;
2). Относительная частота события;
3). Выборочное среднее значение случайной величины.
4. Выборочное среднее равно 19. Интервальная оценка для математического ожидания М может иметь вид
1). (18; 20); 2). (17, 22); 3). (18; 21).
5. Совокупность наблюдений, отобранных случайным образом из генеральной совокупности, называется
| 1). | Репрезентативной | 2). | Вариантой |
| 3). | Выборкой | 4). | Частотой |
6. Объем выборки 1, 2, 2, 2, 3, 3, 4, 4, 6 равен …
7. Математическое ожидание оценки  параметра
параметра  равно оцениваемому параметру. Оценка
равно оцениваемому параметру. Оценка  является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
8. Оценка 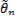 параметра
параметра 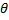 сходится по вероятности к оцениваемому параметру. Оценка
сходится по вероятности к оцениваемому параметру. Оценка 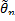 является
является
| 1) | Смещенной | 2) | Состоятельной |
| 3) | Несмещенной | 4) | Эффективной |
9. Произведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 8, 8. Тогда несмещенная оценка математического ожидания равна …
| 1) | 5 | 2) | 6 | 3) | 5,5 | 4) | 5,25 |
10. Выборочная дисперсия вариационного ряда равна 3,5. Объем выборки равен 50. Исправленная выборочная дисперсия равна …
| 1) | 3,43 | 2) | 3,57 | 3) | 0,07 | 4) | 3,5 |
11. Дана выборка объема n. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее 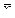 …
…
| 1) | Не изменится | 2) | Увеличится в 25 раз |
| 3) | Уменьшится в 5 раз | 4) | Увеличится в 5 раз |
12. Дан вариационный ряд
| варианта | 1 | 2 | 3 |
| частота | 4 | 2 | 3 |
Величина 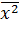 равна …
равна …
13. Дан вариационный ряд
| варианта | 1 | 2 | 3 |
| частота | 5 | 2 | 3 |
Выборочная дисперсия равна …
| 1) | 4 | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
14. Дан вариационный ряд
| варианта | 1 | 2 | 3 |
| частота | 5 | 2 | 3 |
Исправленная выборочная дисперсия равна …
| 1) | 4 | 2) | 1,8 | 3) | 0,84 | 4) | 0,76 |
15. Относительная частота равна 0,25. Гипотеза H 0 для вероятности P
16. 1). 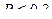 2).
2).  ; 3).
; 3). 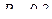 ; 4).
; 4).  ; 5).
; 5). 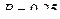 .
.
17. Множеством значений системы двух случайных величин является:
а) промежуток на числовой оси
б) часть координатной плоскости
в) числовая последовательность
18. Статистическим аналогом закона распределения системы двух дискретных случайных величин является
1). Гистограмма; 2). Дисперсия;
3). Корреляционная таблица;
4). Функция распределения вероятности.
19. Какие параметры имеет плотность равномерного закона?
1). Дисперсия; 2). Математическое ожидание;
3). Границы множества значений; 4). Интенсивность потока событий .
20. Дан интервальный вариационный ряд
| варианта | 1-3 | 3-5 | 5-7 | 7-9 |
| частота | 2 | 3 | 4 | 1 |
Выборочная средняя равна…
21. Статистическим аналогом вероятности события является
1). Абсолютная частота события;
2). Относительная частота события;
3). выборочное среднее значение индикатора события.
22. Сумма всех относительных частот дискретного вариационного ряда равна:
1). Значению функции распределения в точке х=1;
2). Вероятности достоверного события;
3). выборочному среднему значению случайной величины.
Дата: 2019-05-28, просмотров: 382.