В качестве характеристики разброса значений количественного признака X вокруг своего среднего значения используется дисперсия.
Определение . Генеральной дисперсией 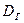 называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения  .
.
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются числовой характеристикой, называемой средним квадратическим отклонением.
Определение . Генеральным средним квадратическим отклонением называют корень квадратный из генеральной дисперсии и обозначают в виде
Пусть для изучения генеральной совокупности относительно количественного признака  произведена выборка объема
произведена выборка объема 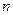 .
.
Определение . Выборочной дисперсией 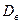 называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочной средней  .
.
Если все значения признака 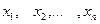 выборки объема
выборки объема  различны, то
различны, то 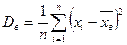 .
.
Если же значения признака 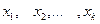 имеют соответственно частоты
имеют соответственно частоты 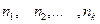 , причем
, причем 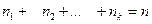 , то
, то 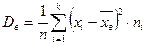 .
.
Определение . Выборочным средним квадратическим отклонением называют корень квадратный из выборочной дисперсии и обозначают в виде
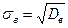 .
.
Записанные выше формулы вычисления выборочной и генеральной дисперсии можно упрости, используя следующую теорему.
Теорема . Дисперсия равна разности между средним квадратов значений признака и квадратом общей средней, то есть
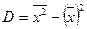 , где
, где 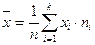 и
и 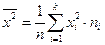 .
.
Пример. Выборочная совокупность задана таблицей распределения
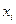
| 1 | 2 | 3 | 4 |
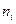
| 20 | 15 | 10 | 5 |
Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение.
Решение.
Найдем выборочную среднюю.
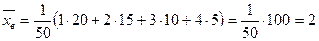 .
.
Найти выборочную дисперсию.
 .
.
Общая средняя уже известна  .
.
Найдем среднюю квадратов значений признака:
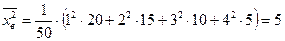 .
.
Тогда 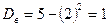 и
и  - это среднее отклонение от среднего значения выборки, то есть от числа
- это среднее отклонение от среднего значения выборки, то есть от числа  .
.
Если в качестве оценки генеральной дисперсии использовать выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. 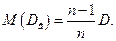
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия
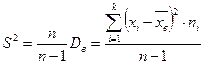
Обе предложенные оценки - выборочная дисперсия и исправленная выборочная дисперсия – являются состоятельными оценками генеральной дисперсии, и разница между ними заметна лишь при небольшом числе наблюдений n. При n > 30 в качестве оценки для D вполне можно использовать Dв. В случае нормально распределенной генеральной совокупности обе эти оценки также являются асимптотически эффективными, т.е. при n→∞ они будут стремиться к эффективной оценке.
Для оценки же среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии и обозначается в виде
 .
.
Пример. Найти выборочную и исправленную дисперсии для следующего статистического распределения
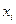
| 1 | 2 | 5 | 8 | 9 |
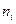
| 3 | 4 | 6 | 4 | 3 |
Решение.
Найдем выборочную среднюю.
 .
.
Найдем выборочную дисперсию по определению.
 .
.
Тогда 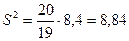 .
.
Дата: 2019-05-28, просмотров: 350.