Чтобы подтвердить некоторые закономер­ности поведения систем при воздействии на них разных соотношений управляющих факторов, уточ­нить и расширить представления о каждом из алго­ритмов, характерных для моделей "А", "В", "Д", разработать убедительные практические рекоменда­ции, было проведено специальное математическое исследование. Цель его состояла в возможности по­лучения математической модели, аппроксимирующей реальный процесс с оптимальной точностью и затра­тами, уменьшения или выделении ошибки экспери­ментальных исследований, возможности принятия решений на основе формализованных правил, оптимизации воздействий в тренировочном процессе для достижения реальных результатов в заданное время.

Представим организм футболиста в виде вектора исходных состояний Z = (Z₁, Z₂, … Z_i,… Z_n), подтверж­денных с определенной точностью задаваемых векто­ром влияющих факторов X = (Х₁-Х₂...Х...Х_n) с (последующей реакцией измеряемых параметров Y = (Y₁-Y_{2, …} Y_{j …} Y_n). Задача состоит в том, чтобы на основании экспериментальных данных каждого пара­метра определить функцию

y_j = f (x, z)                                                        (1)

с определенной точностью аппроксимирующую про­цесс. Это возможно с использованием теории плани­рования эксперимента.

Планом эксперимента называется некоторая мат­рица F (X, Z), строки которой содержат значение факторов и исходных состояний в опыте U}( п = 1 • 2 ..., N ), а столбцы — значение фактора Х_i для исходного состояния Z_l в N опытах. В зависимости от свойства плана эксперимента можно получить поли­ном ( уравнение регрессии) различного порядка:

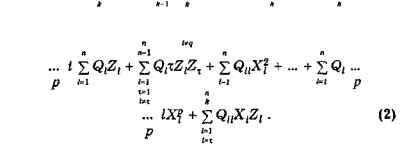
где Q₀, Q_i, Q_ii, ..., Q_i…i — коэффициенты уравнения регрессии нулевого, первого, второго и т.д. порядка соответственно;

Q_ij — коэффициент уравнения регрессии для эф­фекторов взаимодействия факторов Х_1пХ аналогично­го коэффициента уравнения регрессии для исходных состояний;

Q_{1 j} — коэффициент уравнения регрессии для взаи­модействия факторов Х _i и исходного состояния Zi .

Задача нахождения коэффициентов уравнения ре­грессии решается методом наибольших квадратов или в матричной форме:

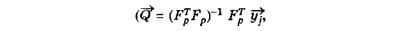
где

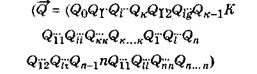
где — F_p расширенная матрица плана эксперимента размера

N_x [1 + Р_к + К (K-1) 2 + Р_n  + П (n-1)*2];

y_j = (y_1j,_, y_2j, y_Nj),

— вектор параметра j в размерах N; Т — знак транспонирования .

Уравнение регрессии для значимых (1) коэффици­ентов проверяется на адекватность результатов экспе­римента полиномом выбранного порядка с помощью F — критерия Фишера.

В случае адекватности представленных результатов уравнение вида (2) принимаем в качестве математи­ческой модели тренировочного воздействия.

Дальнейшее исследование различных воздействий можно проводить по математической модели расчет­ным способом.

Специфика исследования тренировочных процессов определяет круг вопросов, требующих дальнейшего развития или совершенствования нужных функций. Наличие математических моделей существенно упро­щает формализацию поиска оптимальных воздей­ствий на биологическую систему и позволяет использовать для этих целей аппарат нелинейного программирования (2). В этой связи существенно важными являются вопросы формирования целевых функций, введения ограничений на область определе­ния моделей и разработки эффективных процедур оптимизации в условиях сложных взаимодействий параметров (систем).

Значительный интерес представляет поиск опти­мальных условий не только для отдельных парамет­ров, но и для совокупности их (качественных показателей мышечной работоспособности, техничес­кой подготовленности и т.д., т.е. составляющих спе­циальную работоспособность).

Включение в эту совокупность математических мо­делей, связывающих влияние факторов (интенсивно­сти, продолжительности и т.д.) и исходных состояний (сократительной способности мышц, сопротивляемос­ти мышц утомлению, разных дифференцировок, фер­ментов крови и т.д.) на дисперсии параметров, позволяет получить оптимальные результаты с мини­мально допустимой погрешностью.

Для поиска таких условий использовали регуляр­ный алгоритм Нелдера—Мида минимизации функций по деформируемому многограннику с учетом ограни­чений методом штрафных функций (2).

Используя предложенный методологический под­ход по математическому моделированию (3) и опти­мизации (4) необходимых соотношений функцио­нальной активности биологических систем, мы иссле­довали условия для дифференцированного развития качеств, обеспечивающих уровень специальной рабо­тоспособности в игровой деятельности.

Для этого в качестве влияющих факторов выбрали основные структурные элементы управляющих воз­действий:

Х₁— интенсивность выполнения серий игровых действий (- i _у );

Х₂ — продолжительность серий игровых действий ( t _у );

Х₃ — режим чередования серий игровых действий с отдыхом ( t _оп );

Х₄ — количество повторений серий игровых дей­ствий ( k_y ).

В качестве исходных состояний выбрали 10 упра­вляемых систем, на которые воздействовали указан­ные факторы: различные виды дифференцировок ( F , t ,Р), ферменты крови (СДГ, МДГ, ЛДГ, a-ГФДГм, a-ГФДГг), качественные показатели мышечной рабо­тоспособности (ССМ, СМУ), ускорения различных зве­ньев тела, скорость переработки разных видов информации и т.д.

Для примера остановимся на некоторых из них:

Z₁ — сократительная способность мышц (ССМ);

Z ₂ — сопротивляемость мышц утомлению (СМУ);

Zз — ускорение общего центра массы ( q ).

Состояние указанных параметров оценивалось до воздействий и после выполнения серий игровых уп­ражнений в восстановительном периоде (t₀ = О, t₁ = 2, t₂ = 24, t₃ = 30, t₄ = 48, t_Ь = 72 ч отдыха).

В качестве параметров математических моделей использованы те же управляемые системы, но после тренирующих воздействий, которые обозначим: у₁ — ССМ; y₂ — СМУ; у₃ = q.

В силу того, что влияющие факторы и .исходные состояния варьируют в различных диапазонах вели­чин и имеют разные размерности, при матемаатическом моделировании производили их нормирование на интервале (-1, 1) по правилу :

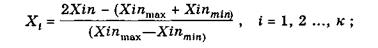
где Хi — нормирование значения фактора; Х _{i п} — натуральное значение фактора; Х in _тах , Х in _{т i} — соответственно максимальное и минимальное значение фактора.

Аналогично проводили нормирование вектора Z:

В математических моделях, таким образом, при­сутствуют только нормированные значения факторов и исходных состояний.

Вычисления коэффициентов регрессии, анализ их значимости и адекватности математическим моделям проводили с помощью программы

В результате получены математические модели, адекватно описывающие влияние тренирующих воз­действий и исходных состояний с вероятностью до 97,5%.

С помощью уравнения регрессии для различных стадий восстановительного периода находили опти­мальные воздействия при заданных исходных состо­яниях для каждого параметра в отдельности и общего критерия параметров, используя программу оптими­зации Simnel на ЭВМ ЕС 1020.

Изложенная выше и апробированная в условиях практики методика моделирования и поиска опти­мальных тренирующих воздействий показала, что во­зможен строго формализованный выбор оптимальных соотношений количественных сторон функциональ­ных биологических систем. При этом оказалось воз­можным создание необходимых состояний в заданное время расчетным путём с учетом временной адапта­ции (срочной и отдаленной).

Как было определено, алгоритм воздействия типа "А" (табл.1) создает соотношение функциональной активности систем, способствующее развитию разных.сторон специальной выносливости (в зависимости от применяемых средств — скоростной, силовой или координационной выносливости).

Таблица 1.