Предположим, что в пространстве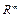 
внешних координат задана некоторая вектор-функция 
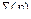вида
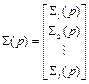=0, (2.79)
где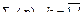 
- дважды дифференцируемые функции своих аргументов.
Тогда говорят, что в пространстве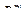 
выражениями (2.79) задано многообразие 
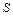[5]. Многообразие 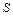может формироваться планировщиком системы управления и отражать желаемые требования к траектории движения манипуляционного робота [6], формируемой в пространстве внешних (базовых) координат.
Дифференцируя по времени выражение (2.79), получим:
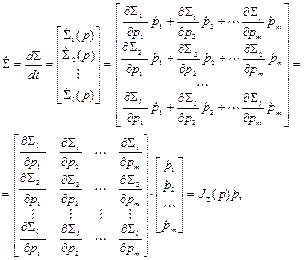(2.80)
здесь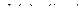 
- матрица Якоби вектора 
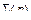(2.79).
Остальные элементы выражения (2.80) определены нами ранее.
Система функций (2.79) будет независимой и, следовательно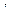 
компонентов вектора 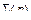действительно определяют в пространстве 
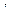-мерное многообразие 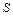, если выполнено следующее условие [5]:
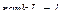, (2.81)
где 
- ранг матрицы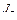 
, 
.
Условие (2.81) соответствует случаю линейной независимости вектор-строк матрицы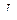 
, которые можно рассматривать как базис натянутого на них 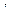-мерного линейного пространства 
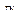, называемого пространством, ортогональным к многообразию 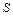в рассматриваемой точке 
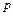[5].
Как записать математическую модель динамики манипуляционного робота в этом пространстве? Используя полученные в предыдущем параграфе результаты, представим модель вида (2.77) в пространстве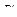 
.
Продифференцируем по времени выражение (2.80):
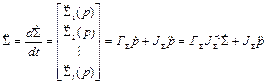, (2.82)
где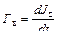 
- 
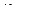-матрица, элементы которой определяются дифференцированием по времени элементов матрицы .
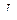Выразим из равенства (2.82) вторую производную по времени от вектора внешних координат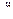 
. В результате получим:
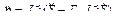. (2.83)
Аналогично выражению (2.72) составим баланс мощностей для пространств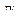 
и
и получим зависимость вектора сил и моментов сил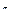 
, действующих на робот в пространстве , с вектором тех же сил и моментов сил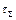 
, но трансформированных уже в пространство :
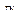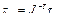, (2.84)
здесь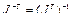 
- матрица, обратная транспонированной матрице Якоби 
.
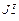Принимая во внимание выражения (2.80), (2.84) и подставив равенство (2.83) в математическую модель динамики робота, представленную в пространстве 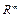, например (2.77), получим:
(2.85)
В случае необходимости, при найденных функциональных зависимостях
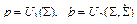
уравнение (2.85) может быть приведено к виду
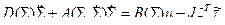. (2.86)
Уравнение (2.86) описывает динамику манипуляционного робота в пространстве .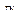
Результаты, изложенные в настоящем параграфе, позволяют синтезировать высокоэффективные алгоритмы управления манипуляционными роботами, не требуя решения обратной задачи кинематики, а структура системы управления может и не содержать интерполяторов и аппроксимирующих устройств [6, 25].
Контрольные задания
Задание № 1. Для кинематической схемы трехзвенного манипуляционного робота, представленной в табл. 1, в соответствии с заданным вариантом, требуется:
а) решить прямую задачу кинематики;
б) определить базовые координаты центра тяжести 3-го звена;
в) решить обратную задачу кинематики для координаты qk, где индекс k определяется по таблице 1.
Кинематические схемы трехзвенных манипуляторов. Табл.1
| Номер варианта | Кинематическая схема | Значение индекса k |
| 1 | 
| 2 |
| 2 | 
| 3 |
| 3 | 
| 3 |
| 4 | 
| 1 |
| 5 | 
| 2 |
| 6 | 
| 1 |
Задание №2. В состав робототехнического комплекса входят два шестизвенных манипуляционных робота МР1 и МР2. Текущее положение рабочего органа МР1, в базовой системе координат, описывается матрицей Т1, а робота МР2 матрицей Т2. В соответствии с данными, представленными в табл.2 и заданным вариантом, требуется определить положение рабочего органа МР2 в системе координат рабочего органа МР1.
Значения матриц Т1 и Т2. Табл.2
| Номер варианта | Значения матриц Т1 и Т2 |
| 1 |
 , 
|
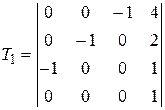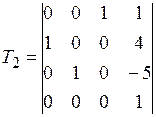
| 2 |
 , 
|
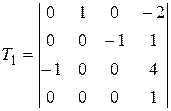| 3 |
 , 
|
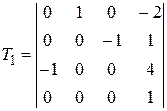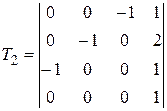
| 4 |
 , 
|
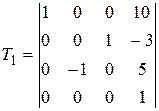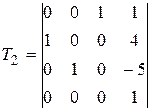
| 5 |
 , 
|
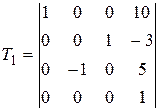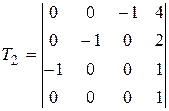
| 6 |
 , 
|
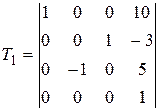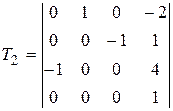
Задание №3. Используя результаты выполнения задания 1, требуется определить следующие элементы уравнения динамики манипуляционного трехзвенника: элементы матрицы инерции Dij, вектора кориолисовых и центробежных сил и моментов hs, вектора гравитационных сил и моментов cl , где значения индексов i , j , s , l определяются по табл. 3, в соответствии с заданным вариантом.
Значения индексов i , j , s , l к заданию №3 . Табл.3
|
Индекс | Номер варианта | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| i | 2 | 3 | 2 | 1 | 3 | 1 |
| j | 1 | 2 | 2 | 1 | 3 | 2 |
| s | 3 | 2 | 1 | 3 | 2 | 1 |
| l | 3 | 2 | 1 | 3 | 1 | 3 |
Библиографический список
1. Попов Е.П., Верещагин А.Ф., Зенкевич С.Л. Манипуляционные роботы. Динамика и алгоритмы.-М.: Наука, 1978.- 400 с.
2. Козырев Ю.Г. Промышленные роботы: Справочник.- М.: Машиностроение, 1983.- 376 с.
3. Фу К., Гонсалес Р., Ли К. Робототехника.- М.: Мир, 1989.-624 с.
4. Denavit J., Hartenberg R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech., 77, p.p. 215-221, 1955.
5. Величенко В.В. Матрично-геометрические методы в механике с приложениями к задачам робототехники. М.. Наука,1988, 288 с.
6. Пшихопов В.Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов// В сборнике РАЕН «Синтез алгоритмов сложных систем», выпуск 9, Москва-Таганрог, 1997, 318 с. С. 93-108.
7. Tchon K., Muszynski R. A normal form solution to the singular inverse kinematic problem for robotic manipulator: the quadratic case. Proc. of the IEEE Inter. Conf. on Robotics and Automation. Leuven, Belgium, 1998, p.p. 3222-3227.
8. Кинематика, динамика и точность механизмов. Справочник./ Под ред. Г.В. Крейнина.- М.:Машиностроение, 1984.- 224 с.
9. Кобринский А.А., Кобринский А.Е. Манипуляционные системы роботов.- М.: Наука, 1985.- 344 с.
10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.- М.: Наука, 1984.- 832 с.
11. Робототехника и гибкие автоматизированные производства. В 9-ти кн. Кн.3. Макаров И.М., Рахманкулов В.З. и др./ Под ред. И.М. Макарова. М.: Высшая школа, 1986.- 159 с.
12. Краснощеков П.С., Петров А.А. Принципы построения моделей. М.: Фазис, 2000.- 412 с
13. Мелентьев Ю.И., Телегин А.И. Динамика манипуляционных систем роботов.- Иркутск: Изд-во Иркутского университета, 1985.- 352 с.
14. Бурдаков С.Ф. Математические модели и дентификация роботов с упругими элементами: Учебное пособие. Л.: Изд-во ЛГТУ, 1990.- 96 с.
15. Уитеккер Э. Аналитическая динамика. - Ижевск: Издательский дом «Ижевский университет», 1999.- 588 с.
16. Краснов М.Л., Кисилев А.И. Макаренко Г.И. и др. Вся высшая математика: Учебник. Т.6.- М.: Едиториал УРСС. 2003.- 256 с.
17. Юревич Е.И. Робототехника: Учебное пособие. СПб.: Изд-во СПбГТУ, 2001.- 300 с.
18. Вукобратович М., Стокич Д., Кирчански Н. Неадаптивное и адаптивное управлении манипуляционными роботами.- М.: Мир,1989. 376 с.
19. Зенкевич С. Л., Ющенко А. С. Управление роботами. Основы управления манипуляционными роботами. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. -399 с.
20. Шахинпур М. Курс робототехники. М.: Мир, 1990.- 527 с.
21. Пол Р. Моделирование, планирование траекторий и управление движением робота-манипулятора. М.: Наука, 1976.- 104 с.
22. Гайдук А.Р. Алгебраические методы анализа и синтеза систем автоматического управления. Ростов-на-Дону: Изд-во РГУ, 1988.- 208 с.
23. Чаки Ф. Современная теория управления.- М.: Мир, 1975.- 424 с.
24. Филипс Ч., Харбор Р. Системы управления с обратной связью.-М.: Лаборатория базовых знаний. 2001.- 616 с.
25. Pshikhopov V. Kh. New Approach to the Design of the Near Time Optimal Path Following Controller for the Manipulating Robots. Proceedings CD (without pages numbers, 6 pages) and Abstracts Book (473 p., p. 353) of Int. Conf. «Mathematical Theory of Network and Systems», Perpignian, France, June 19-23, 2000.
Пшихопов Вячеслав Хасанович
МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАНИПУЛЯЦИОННЫХ РОБОТОВ
Редактор
Корректор
Подписано к печати
Офсетная печать Усл. п.л. – 6,6 Уч.-изд.л. – 6,2
Заказ № Тираж 500
“С”
Издательство
Дата: 2019-04-23, просмотров: 209.
