Предположим, что известны массы и моменты инерции двигателей и передаточных механизмов, осуществляющих перемещение звеньев манипуляционного робота, а также их параметры, позволяющие записать математическую модель исполнительного механизма в виде следующего векторно-матричного уравнения:

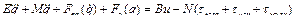,…. (2.62)

где 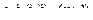 - векторы соответственно обобщенных координат, скоростей, ускорений и третьей производной по времени от ;

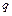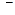- диагональная матрица известных коэффициентов, ; 

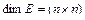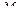 - диагональная матрица приведенных моментов и масс собственно двигателей и передаточных механизмов, ;

а

б

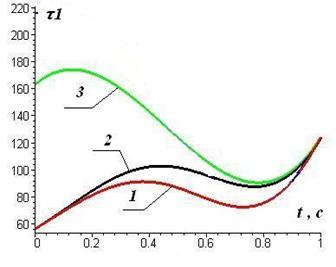
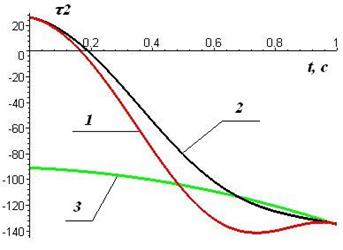
Рис.2.8. Силыи моменты сил в сочленениях при различных методах упрощения модели: а) - в 1-м сочленении; б) - в 2-м сочленении, здесь 1- полная модель; 2- модель, упрощенная по Полу; 3- модель, линеаризованная в конечной точке

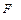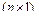 - -вектор известных функций сил вязкого трения;

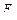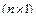 - -вектор известных функций сил и моментов сил демпфирования;

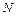 - диагональная матрица передаточных отношений дополнительных механизмов (редукторы, червячные передачи и т.п., для пневмо- и

гидроприводов это, как правило, единичная матрица). Например, для 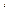- й редукторной передачи 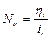, здесь 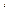- передаточное число, 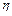- кпд редуктора;

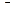 - диагональная матрица коэффициентов управления, ;

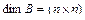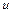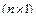 - -вектор управляющих воздействий;

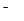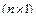- -вектор обобщенных сил и моментов, приведенных к осям соответствующих сочленений и вызванных механической системой манипулятора. По существу, вектор  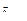однозначно определяется из уравнения динамики (2.25), = ;

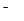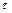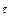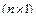- -вектор измеряемых дополнительных возмущений (например, измеряемых силомоментными датчиками), приведенных к осям соответствующих двигателей;

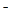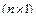- -вектор неизмеряемых возмущений (вязкое трение механической системы робота в среде, неизмеряемые нагрузки силового взаимодействия со средой и т.п.), приведенных к осям соответствующих двигателей;

здесь 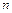- число степеней подвижности манипуляционного робота.

С учетом принятых положений о динамике двигателей и полученного ранее уравнения динамики механической системы (2.25) полная динамика робота может быть представлена следующим матричным выражением:

.(2.63)

Или, сгруппировав элементы уравнения (2.63) по степени производной по времени от вектора 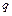, получим:

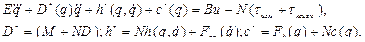 (2.64)

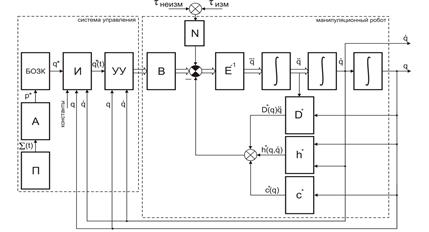
Структурная схема манипуляционного робота, соответствующая уравнению (2.64), представлена на рис. 2.9.

При допустимости предположения, что 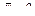 (например, для двигателей постоянного тока), справедливо следующее уравнение динамики манипуляционного робота с учетом двигателей:

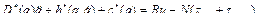              (2.65)

При малых значениях коэффициентов передачи передаточных механизмов (до 10) влияние динамики приводов на общую динамику манипуляторов незначительно и для описания полной модели динамики робота, в левой части уравнений (2.63)-(2.65), достаточно учитывать только динамическую модель его механической системы.