С точки зрения динамики всякая материальная система состоит из материальных точек, связанных различного рода связями. Так, твердое тело можно рассматривать как систему материальных точек, которые при помощи соответствующих внутренних сил реакции удерживаются, при принятых допущениях, на неизменных расстояниях друг от друга.
Если известно строение такого рода системы, как-то: форма, величина и масса ее частей, то конфигурация системы в любой момент времени может быть задана как функция определенных величин, изменяющихся при изменении конфигурации. Эти величины называются координатами системы. Мы будем обозначать число координат, необходимых для определения конфигурации механической системы манипуляционных роботов, через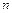 
. Сами координаты мы будем обозначать через 
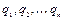и понимать под ними обобщенные координаты, рассмотренные в предыдущем разделе.
В механике различают двоякого рода динамические системы, различие которых весьма существенно при аналитическом исследовании движения. Это различие мы поясним на простом примере [14].
Рассмотрим движение шара данного радиуса, который при своем движении все время касается некоторой неподвижной плоскости, которую мы примем за плоскость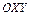 
. Положение шара в каждое мгновение вполне определяется пятью координатами: двумя прямоугольными координатами 
центра шара и тремя углами Эйлера 
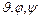, определяюшими вращение шара вокруг своего центра. Шар может занимать любое положение, при котором он сохраняет соприкасание с плоскостью, поэтому все пять координат 
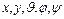могут принимать любые значения.
Если плоскость - гладкая, то перемещение из положения с координатами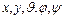 
в бесконечно близкое положение, определяемое координатами 
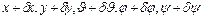где,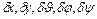 
- любые бесконечно малые величины, является возможным перемещением, т. е. шар может выполнить это перемещение без нарушения наложенных на него связей. Но если плоскость является абсолютно шероховатой, то это перемещение при произвольных 
не будет возможным. В самом деле, перемещение точки касания (с точностью до величин порядка выше первого) должно равняться нулю, и поэтому величины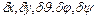 
не являются более независимыми. В рассматриваемом случае эти величины удовлетворяют двум неинтегрируемым линейным дифференциальным уравнениям. Таким образом, для шара, находящегося на абсолютно шероховатой плоскости, перемещение, определяемое произвольными бесконечно малыми изменениями координат, не является обязательно возможным.
Система называется голономной, если всякое перемещение, определяемое любым бесконечно малым изменением координат, является возможным (например, шар на гладкой плоскости), в противном случае система называется неголономной (например, шар на шероховатой плоскости).
Голономные системы характеризуются, следовательно, тем, что для них число степеней свободы всегда равно числу независимых координат, необходимых для определения конфигурации системы.
Рассмотрим движение голономной системы с 
степенями свободы. Обозначим через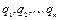 
координаты системы, определяющие ее конфигурацию в момент времени 
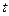, и через 
- координаты какой-нибудь точки массы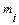 
относительно базовой системы координат. Эти базовые координаты, посредством решения прямой задачи кинематики, являются известными функциями величины 
.
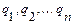Пусть эти функции представляются выражениями, полученными в результате решения прямой задачи кинематики:
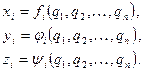
Если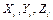 
означают компоненты равнодействующей всех сил (как внутренних, так и внешних), действующих на точку 
, то уравнения движения этой точки имеют вид
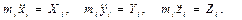
Умножим эти уравнения соответственно на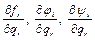 
, а затем сложим их и просуммируем по всем точкам системы. Тогда получим:
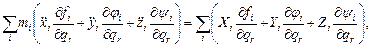
где знак 
означает суммирование по всем точкам системы, следовательно, либо интегрирование, либо суммирование по некоторому конечному числу точек.
Но
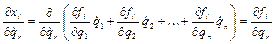
и поэтому
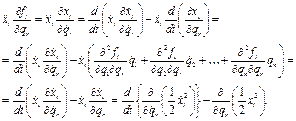
Отсюда
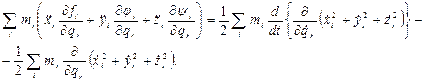
Выражение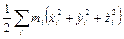 
, представляющее собой полусумму произведений массы каждой отдельно взятой точки на квадрат ее скорости, называется кинетической энергией системы. В силу того, что структура системы нам известна, мы можем кинетическую энергию выразить как функцию величин 
.
Мы будем ее в дальнейшем обозначать через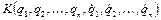 
и будем предполагать, что она нам известна как функция своих аргументов. Так как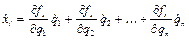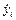
и 
и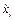 
суть также линейные функции от 
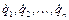, то 
есть квадратичная функция от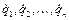 
. Функци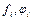и 
и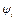 
не содержат явно времени (что представляется всякий раз, когда связи системы не зависят от времени) и 
являются однородными линейными функциями от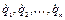 
, и будет однородной квадратичной функцией относительно тех же аргументов.
Кинетическая энергия системы в силу самого ее определения существенно положительна, следовательно,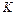 
есть определенная положительная квадратичная форма относительно 
.
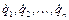Из уравнений движения мы получим, таким образом, следующее уравнение:
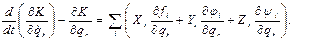
Левая часть этого уравнения не зависит явно от координат отдельных точек системы. Попытаемся и правую часть привести к такой же форме. Для этой цели сообщим системе перемещение, при котором координата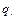 
принимает значение 
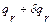, а остальные координаты остаются неизменными. Так как система голономна, то такое перемещение возможно без нарушения связей. Координаты точки 
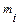принимают при таком перемещении значения
Поэтому сумма работ всех сил, действующих на систему, равна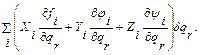 
Все силы, приложенные к системе, за исключением тех, которые не производят работы, называются внешними. Отсюда следует, что выражение 
представляет собой сумму работ внешних сил при перемещении, в котором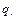 
переходит в 
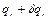, а остальные координаты остаются неизменными. Так как структура системы и приложенные силы нам известны, то эта величина есть известная функция от 
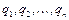. Обозначим ее через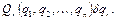 
Тогда будем иметь:
.
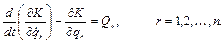Мы получили, таким образом, 
обыкновенных дифференциальных уравнений второго порядка, в которых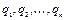 
являются зависимыми, а 
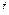- независимой переменными. Так как число уравнений равно числу зависимых переменных, то теоретически этих уравнений достаточно для определения движения при заданных начальных условиях. Резюмируя, мы можем полученный результат высказать следующим образом [15]
|
- кинетическая энергия системы, a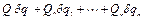 
─ работа приложенных к ней внешних сил при произвольно выбираемом перемещении 
, где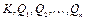 
в силу известности структуры системы суть известные функции от 
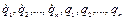. Тогда уравнения движения системы могут быть записаны в виде
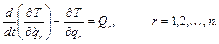
Эти уравнения называются уравнениями Лагранжа (в вариационном исчислении – уравнениями Эйлера [16]).
Некоторые силовые поля обладают тем свойством, что работа сил этих полей при движении динамической системы зависит лишь только от начального и конечного положений системы. Другими словами, работа имеет одно и то же значение независимо от того, из какой последовательности бесконечно малых перемещений складывается конечное движение.
Такого рода силовым полем является, например, поле силы тяжести. Как известно, работа силы тяжести при перемещении материальной точки массы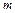 
из положения, имеющего высоту 
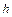, в положение с высотой 
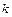равна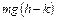 
, т. е. не зависит от пути, по которому точка перешла из первого положения во второе.
Такого рода силовые поля называются консервативными. Пусть конфигурация системы определяется координатами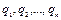 
. Примем какую-нибудь определенную конфигурацию, например соответствующую координатам 
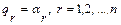, за основную. Если внешние силы, действующие на систему, - консервативны, то работа этих сил при перемещении системы из конфигурации 
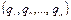есть определённая функция от 
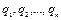, не зависящая от вида перемещения. Эта функция, обозначаемая в дальнейшем через 
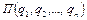, называется потенциальной энергией системы в конфигурации 
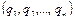. Работа внешних сил при бесконечно малом перемещении 
равна, очевидно, бесконечно малому уменьшению функции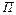 
, т. е. выражению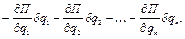 
В силу этого уравнения Лагранжа принимают вид
,
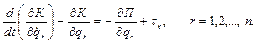где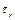 
- обобщенные силы и моменты , действующие в 
-м сочленении.
Вводя новую функцию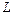 
от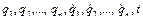 
при помощи равенства
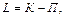мы можем эти уравнения привести к виду
(2.1)
Функция 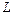называется кинетическим потенциалом, или функцией Лагранжа.
В качестве примера использования уравнения (2.1) рассмотрим вывод уравнений динамики материальной точки M массой m, находящейся в поле силы тяготения. Пример поясняется рис. 2.1, где OXYZ – неподвижная, базовая система координат, а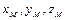 
- соответствующие координаты точки M.
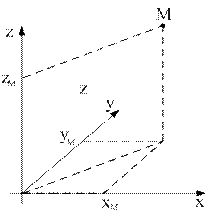
Рис.2.1. К примеру использования уравнений Лагранжа-Эйлера
Из курса физики известно, что потенциальная энергия этой точки определяется выражением
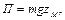
где g- величина ускорения свободного падения.
А кинетическая энергия этой же точки определяется выражением
.
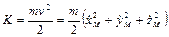Соответственно функция Лагранжа имеет вид
.
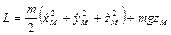Дифференцируя соответствующим образом функцию Лагранжа для материальной точки, получим следующие промежуточные выражения:
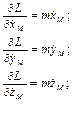
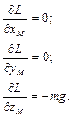
В соответствии с уравнением Лагранжа-Эйлера (2.1) имеем
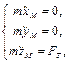(2.2)
где FT - сила тяжести, действующая на материальную точку.
Очевидно, что система уравнений (2.2) представляет собой запись второго закона Ньютона для материальной точки, находящейся в поле сил тяготения, и демонстрирует фундаментальную связь между лагранжевой и ньютоновой механикой.
2.2. Скорость произвольной точки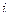 
-го звена манипулятора
Частные производные матриц преобразования однородных координат по обобщенным координатам и скорость произвольной точки механической системы манипулятора
Прежде, чем перейти к использованию уравнения Лагранжа-Эйлера (2.1) для описания динамики механической системы манипуляционных роботов, определим скорость произвольной точки манипулятора в терминах матриц однородных преобразований, используемых в предыдущем разделе. Скорости необходимо знать для определения кинетической энергии рассматриваемой физической системы.
Рассмотрим кинематическую схему произвольного манипуляционного робота, введем базовую систему координат 
и определим скорость точки, неподвижной относительно i-го звена, с учетом движения всех сочленений манипулятора (рис 2.2).
Выберем произвольную точку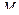 
на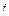 
-м звене, координаты которой в жестко связанной с 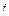-м звеном системе координат 
определены как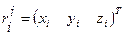 
. Тогда в базовой системе координат 
координаты 
этой же точки 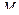можно определить следующим образом:
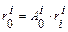, (2.3)
где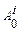 
– матрица преобразований однородных координат, определяющих пространственное положение системы координат 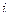- го звена относительно базовой системы координат.
Дифференцируя по времени выражение (2.3), скорость точки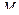 
в базовой системе координат 
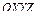определим следующим выражением:
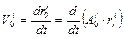. (2.4)
Но, в силу выражения (1.34),
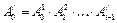(2.5)
В результате имеем: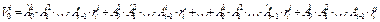 
(2.6)
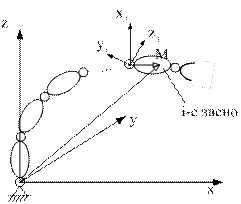
Рис.2.2. Кинематическая схема произвольного манипуляционного робота
В рамках предположения о том, что звенья манипулятора представляют собой твердые тела, точка 
так же, как и любая другая точка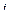 
-го звена, имеет нулевую скорость относительно 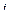-й системы координат, скорость точки 
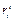относительно базовой системы координат может быть представлена следующим образом:
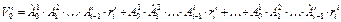. (2.7)
Поскольку каждая из матриц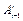 
, входящих в выражение (2.7), является функцией только лишь одной обобщенной координаты 
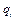, то (2.7) может быть представлено в виде
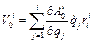. (2.8)
Частные производные матрицы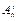 
по переменным 
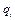легко вычислить с помощью матрицы 
[3], которая для вращательного сочленения имеет вид
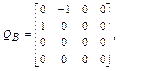(2.9, а)
а для поступательного сочленения
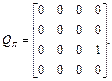(2.9, б)
Используя эту матрицу, можно написать
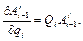(2.10)
Таким образом, для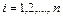 
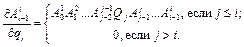(2.11)
По смыслу равенства (2.11) описывает изменение положения точек 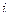-го звена, вызванное движением в 
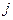-м сочленении манипулятора. Для упрощения формул введем обозначение 
с учетом которого равенство (2.11) можно представить в следующем виде для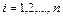 
:
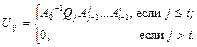(2.12)
Используя введенное обозначение, формулу (2.7) для вычисления скорости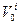 
можно представить в форме
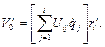(2.13)
Следует отметить, что частная производная матрицы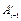 
по переменной 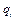уже не является матрицей преобразования однородных координат. Если рассматривается вращательное сочленение, то умножение матрицы 
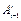слева на матрицу 
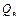эквивалентно перестановке первых двух строк матрицы 
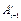с последующим изменением знака всех элементов первой строки на противоположный и обнулением всех элементов третьей и четвертой строк. Для поступательного сочленения эффект такого умножения, с использованием матрицы 
, состоит в перестановке третьей и четвертой строк матрицы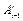 
и последующем обнулении элементов всех строк, кроме третьей. Смысл использования матриц 
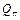и 
состоит в том, чтобы сохранить в формулах матрицы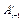 
и все операции производить только с ними [3].
Определим величину, характеризующую эффект взаимодействия сочленений, следующим образом [3]:
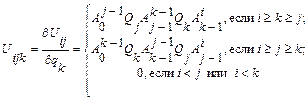(2.14)
Например, для манипулятора с вращательными сочленениями при i = j = k =1 имеем
Дата: 2019-04-23, просмотров: 382.
