Анализ динамических свойств механических систем манипуляторов на примере трехзвенника. Кубические сплайны и их использование при анализе динамики

Уравнения динамики манипуляционных систем используются при синтезе их систем управления и при анализе кинематических схем манипуляционных роботов. Вопросы синтеза выходят за рамки данного пособия и достаточно подробно рассмотрены в работах [3, 6, 14, 17, 18, 19]. В этом параграфе рассмотрим только элементы предварительного анализа динамических моделей на примерах уравнений, полученных в п. 2.7.

Из указанных уравнений видно, что величины обобщенного момента τ _i зависят не только от закона изменения i - й обобщенной координаты робота, но и от закона изменения всех остальных координат. Динамическая связность степеней подвижности приводит к дополнительным нагрузкам на двигатели и, в принципе, является нежелательным фактором. Попытаемся на примере механической системы трехзвенника, рассмотренного в предыдущем параграфе и описываемого выражениями (2.37), (2.44), (2.45) и (2.46), выявить причины этой взаимосвязанности и оценить возможность ее полного или частичного устранения.

Анализируя матрицу инерции (2.44), легко установить, что приведенный к оси первого сочленения момент инерции зависит от значений координаты q _3. Диапазон изменений параметров, вызванных изменением конфигурации механической системы робота, может быть весьма широким: отношение максимального момента инерции к минимальному во многих существующих роботах может достигать 10 и более. Естественно, это приводит к соответствующему диапазону изменения приведенных моментов, возникающих при отработке заданных программ изменения соответствующих обобщенных координат. Устранение этого влияния на конструктивном уровне является чрезвычайно сложной задачей. Так, например, возможно увеличение постоянных компонент моментов инерции звеньев для ослабления влияния на динамику механической системы их переменных частей, но такой вариант неприемлем для приводов, поскольку он приводит к снижению быстродействия системы и увеличению нагрузок при разгоне и торможении звеньев манипулятора. Наиболее целесообразным, в этих случаях, является возможно более полный учет переменных частей приведенных моментов инерции звеньев в моделях динамики, используемых в процедурах синтеза управлений.

Кроме того, инерционные силы, приведенные к оси первого сочленения, определяются ускорением, создаваемым в третьем сочленении, с коэффициентом пропорциональности am ₃. В силу симметричности матрицы 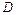, тот же коэффициент пропорциональности обуславливает наличие инерционных сил, возникающих в третьем сочленении, которые обусловлены ускорением в первом сочленении. Очевидно, что для исключения взаимовлияния степеней подвижности по этому каналу целесообразно изменить конструктивные параметры манипулятора таким образом, чтобы параметром a стал равен нулю.

Из выражения (2.45) следует, что изменение обобщенной скорости в третьем сочленении приводит к изменению обобщенного момента в первом сочленении в силу возникающей при движении манипулятора кориолисовой силы. Кроме того, в третьем сочленении возникает дополнительный момент, обусловленный центробежной силой, пропорциональной квадрату обобщенной скорости в первом сочленении. Указанная динамическая взаимосвязь определяется скоростями в соответствующих сочленениях и при их малых значениях может и не оказывать существенного влияния на общую динамику механической системы. При повышении требований к производительности робота будет возрастать и значимость этих составляющих динамики.

Что касается гравитационных сил и моментов, действующих в i-ом сочленении манипулятора, то, в общем случае, они также зависят от значений обобщенных координат в других сочленениях механической системы. В данном случае, в соответствии с выражениями для элементов вектора c (2.46), степени подвижности трехзвенника развязаны по этой составляющей динамической модели.

Следует отметить, что полное разделение степеней подвижности манипуляторов посредством изменения конструктивных параметров достигается в весьма редких случаях (например, в роботе с тремя поступательными сочленениями, оси которых взаимно перпендикулярны, или при организации парциальных движений, когда управление манипулятором осуществляется в данный момент времени только по одной из обобщенных координат, что, естественно, приводит к снижению производительности робота).

Помимо приведенного анализа уравнений динамики, выражения (2.37), (2.44), (2.45) и (2.46) могут быть использованы для корректного выбора исполнительных двигателей по моменту и передаточных механизмов. Для этого следует построить графики обобщенных моментов, действующих в сочленениях роботов, и их максимальное по модулю значение разделить на кпд η механизма (например, для редуктора η=0,8-0,9). Графики моментов обычно строят с использованием интерполирующих полиномов-сплайнов [20], определяющих закон изменения координаты q_i в i - м сочленении. Известно множество подходов к формированию сплайнов [20], которые являются полиномами в функции времени и, по существу, представляют собой задающие воздействия на соответствующие приводы манипулятора.

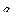Рассмотрим процедуру построения наиболее простых – кубических сплайнов , входными параметрами для которой являются задаваемые значения обобщенных координаты и скорости 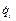в начальный  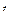и конечный  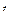 моменты времени: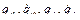

Тогда полином 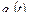, удовлетворяющий заданным граничным условиям, имеет вид

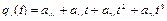,                 (2.47)

где значения коэффициентов 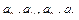 при 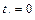 и определяются выражениями:

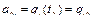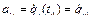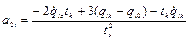, , ,                                      (2.47, а) , .

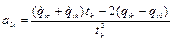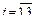           Соответственно, первая и вторая производные по времени полинома (2.47) имеют вид

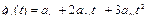,                                       (2.48)

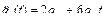 .                                                   (2.49)

Естественно, при формировании полиномов (2.47) необходимо учитывать кинематические и динамические ограничения, а также расположенные в рабочей зоне манипулятора препятствия.

Зададим следующие численные значения граничных условий по обобщенным координатам и скоростям и t_k для всех трех звеньев рассматриваемого трехзвенника: t_k =1 , q ₁₀ =0, q ₂₀ =0, q ₃₀ =0, q _{1 k} =2π, q _{2 k} =0,8, q _{3 k} =0,5, 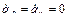, 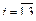. Тогда, в силу выражений (2.47), имеем

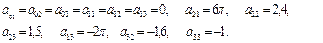(2.50)

Подставим полученные коэффициенты (2.50) в интерполирующие функции (2.47)-(2.49), которые, в свою очередь, подставим в выражения (2.37), (2.44), (2.45), (2.46), и вычислим возникающие моменты τ _i , задав следующие конструктивные параметры манипулятора: m ₁=20, кг; m ₂=12, кг; m ₃=6, кг; a=0,3, м; l ₁=1, м; l ₂=0,4, м; l ₃=0,15, м; r ₁=0,15, м.

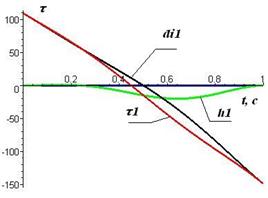
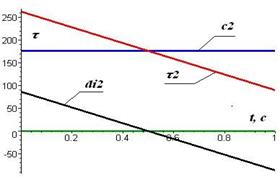
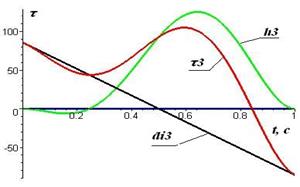
Графики моментов и сил, возникающих в сочленениях трехзвенника, представлены на рис. 2.7, где τ _i – обобщенный момент в i-м сочленении; di_i – момент инерционных сил в i-м сочленении; h_i- момент кориолисовых и центробежных сил в i-м сочленении; c_i – гравитационные силы и моменты в i-м сочленении . Очевидно, что кориолисовы силы не оказывают существенного влияния на динамику первого сочленения, но, с другой стороны, существенно влияют на третье сочленение и должны быть учтены при упрощении исходной модели. Обобщенный момент τ₁ и его составляющие могут быть корректно линеаризованы. Момент τ₂ отражает линейный характер динамики второго сочленения.

а

б

Рис. 2.7. Силы и моменты сил в сочленениях манипуляционного трехзвенника: а) в 1-м сочленении; б) во 2-м сочленении; в) в 3-м сочленении, где τ i – обобщенный момент, dii - инерционные силы и моменты, ci -гравитационные силы и моменты hi - кориолисовы и центробежные силы и моменты в i -м сочленении