Рассмотрим представленный на рис. 2.6 трехзвенник с произвольными сочленениями и получим расчетные формулы для вычисления динамических коэффициентов 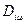, , 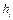 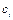в соответствии с рассмотренными ранее формулами (2.26) - (2.28).

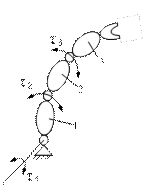
Рис. 2.6. Общий вид манипуляционного трехзвенника

В соответствии с выражением (2.25) уравнение динамики в матричной форме имеет вид

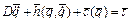,                                           (2.37)

где .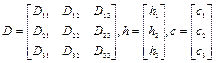

Соответственно, в скалярной форме уравнения (2.37) принимают вид

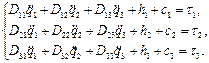                (2.38)

Определим динамические коэффициенты, входящие в уравнения (2.37) и (2.38). В соответствии с выражением (2.26) имеем:

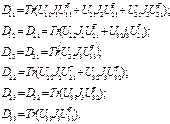                           (2.39)

Определим вспомогательные матрицы :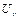

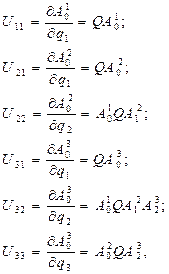                     …..(2.40)

где матрица 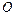 выбирается по выражениям (2.9) в соответствии с характером сочленения, по координате которого производится дифференцирование.

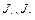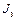Процедура построения  и  рассмотрена в п. 2.3.

Определим элементы вектора кориолисовых и центробежных сил и моментов, используя выражение (2.27):

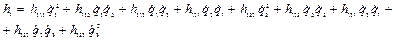(2.41)

При 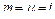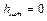. Следовательно,  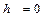и 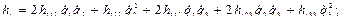.(2.41, а)

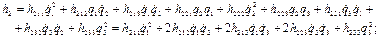(2.41,б)

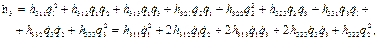(2.41, в)

где

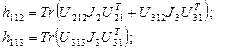
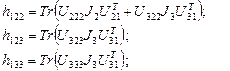
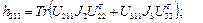……………………………(2.41-г)

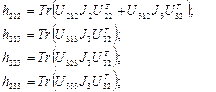
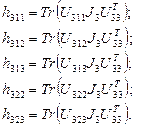
Определим вспомогательные матрицы 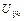, используя выражение (2.14):

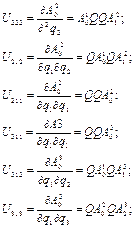                                                ……….(2.42)

,

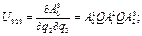
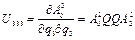где матрица 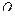 выбирается по выражениям (2.9) в соответствии с характером сочленения, по координате которого производится дифференцирование.

Для определения вектора 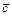 гравитационных сил и моментов используем выражение (2.28):

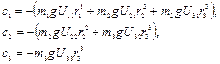                   (2.43)

Пример 2.2. Требуется определить коэффициенты уравнений динамики трехзвенника, представленного на рис. 1.12, если известны его матрицы однородных преобразований (см. п.1.7) и масса 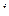-го звена равна 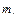. Тип кинематических сочленений и габаритные параметры определены на рис. 1.2.

Решение.

Уравнение динамики трехзвенника имеет вид (2.37).

1. Определим коэффициенты матрицы инерции 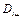, используя выражение (2.39) и (2.40).

Определим вспомогательные матрицы 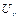 по выражениям (2.40).

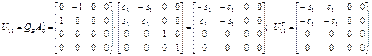
Аналогичным образом имеем:

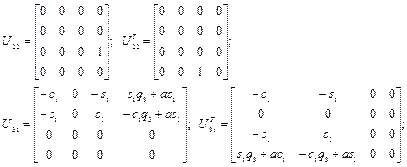
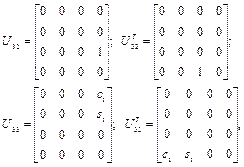
где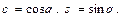

Получим матрицы инерции  соответствующих звеньев по правилам, изложенным в п. 2.3:

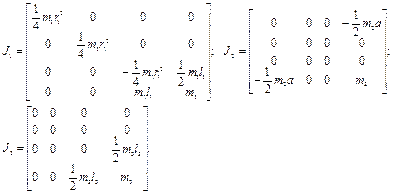
Тогда в соответствии с выражениями (2.39) имеем:

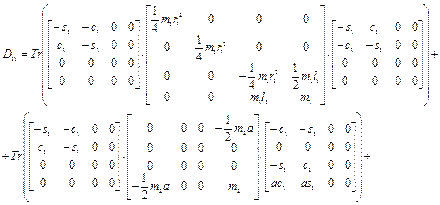
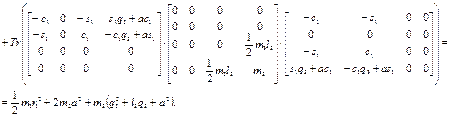
Аналогичным образом имеем:

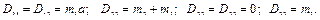
Таким образом, матрица инерции 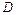 манипулятора имеет вид

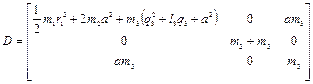. (2.44)

2. Определим элементы вектора 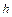 центробежных и кориолисовых сил, используя выражения (2.41). Определим вспомогательные матрицы  по выражениям (2.42).

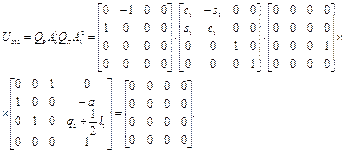
Аналогичным образом имеем:

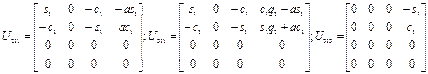
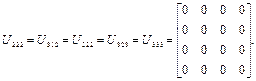
Используем теперь выражения (2.41) для определения элементов .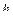

Поскольку матрицы 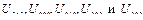являются нулевыми, то соответственно равны нулю и элементы  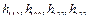в выражении (2.41-а) и следовательно ,

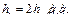где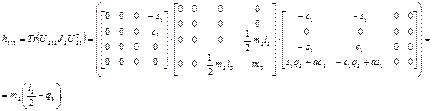

Аналогичным образом можно показать, что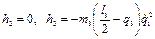

и, соответственно 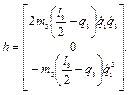                           ………… (2.45)

3. Посредством выражений (2.43), определим элементы 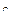 вектора  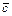гравитационных сил и моментов, действующих в сочленениях рассматриваемого трехзвенника.

В соответствии с расположением осей базовой системы координат 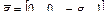, здесь .

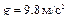В соответствии с рис.1.12 зададим координаты центров тяжести звеньев в связанных с этими звеньями системах координат следующими векторами:

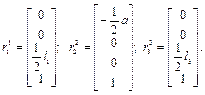
Определим элементы вектора  гравитационных сил и моментов, используя выражение (2.43) и вспомогательные матрицы, полученные в п.1 настоящего решения. В результате имеем:

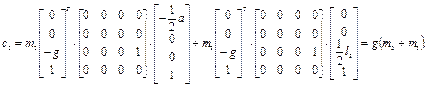
Можно показать, что элементы 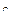 и 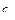 равны нулю, т.е.

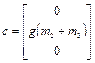.                                       (2.46)