Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

К численным методам решения ОЗК, получившим наибольшее распространение, относится метод Ньютона и методы, основанные на процедурах градиентного поиска.

Поясним содержание метода Ньютона на примере скалярной функции.

Пусть задано некоторое уравнение функции F* своего аргумента x вида F*(x)=0. Тогда решение этого уравнения может быть определено в численном виде посредством итерационной процедуры, записываемой в виде следующего выражения [10]:

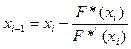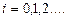,   ,                (1.49)

где .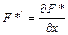

Выражение (1.49) определяет содержание метода Ньютона. Задается искомое решение исходного уравнения (его корень) произвольным образом и оно же выбирается в качестве нулевого приближения x₀. Вычисляется 1-е приближение корня по выражению (1.49), которое на втором шаге подставляется в правую часть выражения (1.49), позволяя вычислить 2-е приближение искомого корня и т.д. Причем выход из процедуры (1.49) определяется заданной погрешностью вычислений Δ и может быть осуществлен, например, при выполнении неравенства ‌ x_{i +1} - x_i ‌ < Δ.

Пусть, например, F*(x)=4x-20=0. Решение этого уравнения очевидно: x=5. Но попытаемся найти его, используя метод Ньютона. Поскольку 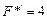, то выражение (1.49) может быть представлено в виде

.

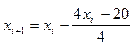В качестве нулевого приближения при i=0 примем x₀=20. Подставим его в последнее равенство. Имеем: x₁=5. Т.е. уже на первом шаге процедуры искомое решение найдено.

50

Вернемся к решению ОЗК. Предположим, что решение ПЗК известно и заданы желаемые координаты рабочего органа МР в пространстве внешних координат p _ж. Тогда, в силу выражения (1.1), мы можем сформировать векторную функцию I вида

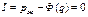,                                            (1.50)

корни которой и являются искомым решением ОЗК.

Тогда, в соответствии с выражением (1.49), получим:

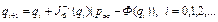,              (1.51)

где J _Ф- матрица Якоби решения ПЗК, определенная нами в п. 1.8.2.

Рассмотрим использование выражения (1.51) на примере манипуляционного робота с цилиндрической системой координат.

Пример 1.12. Пусть требуется решить ОЗК для МР с цилиндрической системой координат для желаемого положения схвата, заданного вектором P _ж = (-0,233, 0,596, 0,650)^Т. Используем выражение (1.51), приняв q ₀ = (80^o, 0,8 м, 0,13 м)^Т. Число шагов итерации определяется погрешностью позиционирования схвата, которая по каждой из внешних координат не должна превышать 1 мм.

Решение. Используем решение ПЗК (1.38) для рассматриваемого МР, полученное нами в п.1.7. Матрица Якоби данного манипулятора определена в примере 1.11, п. 1.8.2. Результаты использования процедуры (1.51) приведены в табл. 4. 

Таблица 4

Результаты решения ОЗК методом Ньютона

Значения

Параметра

Шаг итерации

0 1 2 3 1, град 80 54,132 60,923 59,989 q 2, м 0,8 0,600 0,600 0,600 q 3, м 0,13 0,179 0,094 0,100 Δx , мм 195 -16 7 0 Δy , мм 145 43 2 0 Δz , мм -200 0 0 0

 

Из табл. 4 видно, что обобщенные координаты принимают значения q=(59,989, 0,6, 0,1)^Т, удовлетворяющие поставленной задаче, уже на 3-м шаге итерации. Результаты решения ОЗК согласуются с полученными нами в примере 1.10, п. 1.8.1.

Следует отметить, что в области больших отклонений нулевого приближения от истинного значения корней уравнения (1.50), процедура, основанная на выражении (1.51), может и не дать устойчивых решений. Кроме того, найденные в результате итераций значения могут и не принадлежать области допустимых значений аргумента. Так, например, уже при q₁₀=90^o использование метода Ньютона дает значение q₃=0,899, что невозможно в силу конструктивных особенностей рассматриваемого манипулятора, поскольку должно соблюдаться очевидное условие: q₃<l₄=0.5. Поэтому при больших начальных отклонениях аргумента рассматриваемых функций от искомых значений их корней используются градиентные методы [10].

52

Суть градиентных методов заключается в пошаговом приближении к решению уравнения (1.50) в соответствии с выражением

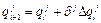,                              (1.52)

где 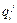- i-е приближение j- й координаты; δ- «направление» i-го шага; Δ 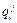- величина i-го шага по j- ой координате.

Причем значения δ и Δ 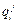 выбираются таким образом, чтобы минимизировать значения функции 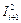. Т.е. требуется выполнение следующей последовательности неравенств:

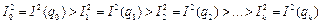 , (1.53)

здесь k- конечный шаг итерации.

В этом случае функция I (1.50) называется функцией невязки. Получаемые промежуточные значения обобщенных координат 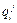могут быть использованы при формировании траектории перехода j-го звена из точки 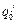в точку 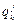, определяемую желаемым положением рабочего органа МР.

Естественно, при использовании численных методов решения ОЗК на каждом шаге итерации, необходимо удовлетворять ограничениям, накладываемым на обобщенные координаты и ориентацию рабочего органа МР, а также учитывать наличие препятствий, расположенных в рабочем пространстве манипулятора.

Для более детальной проработки вопросов, связанных с решением ОЗК, рекомендуется литература [3, 11].

Следует отметить, что в работе [6] предложены подходы к управлению манипуляционными роботами, не требующие решения обратной задачи кинематики.