Рассмотрим математическую модель механической системы безызбыточного манипуляционного робота с n звеньями следующего вида:

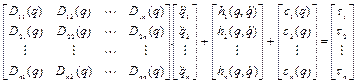,.(2.51)

здесь обозначения имеют тот же смысл, что и в выражении (2.25).

Полную математическую модель механической системы манипулятора вида (2.51) можно непосредственно использовать при формировании алгоритмов управления роботами [6], синтезируя их в классе нелинейных систем. Такой подход позволяет учесть нелинейные свойства динамических моделей манипуляционных роботов, обеспечивая тем самым высокую точность при отработке быстрых траекторий. С другой стороны, вычисление всех динамических коэффициентов модели (2.51) требует дополнительных вычислительных затрат при формировании управляющих воздействий с заданной частотой и оправдано при дополнительных требованиях к точности отработки роботом спланированных траекторий.

Что касается решения прямой задачи кинематики (1.1), которая, наряду с моделью динамики (2.51) и решением обратной задачи кинематики (1.2) является одним из основных элементов математических моделей манипуляционных роботов, то для обеспечения точности отработки заданий роботом ее обычно не упрощают и используют в виде (1.37).

При решении ряда задач управления роботом (например, позиционирования, т.е. вывода в заданную точку с нулевой скоростью), когда не требуется высокой точности позиционирования, модель динамики (2.51) может быть упрощена, что, естественно, упрощает и структуру регуляторов системы управления.

 Существует множество подходов к упрощению динамической модели манипуляционного робота. Рассмотрим некоторые из них.

Упрощенная линеаризация. При таком подходе недиагональные элементы матрицы инерции D обнуляются, диагональные элементы вычисляются в целевой точке (точке позиционирования), а элементы h_i вектора кориолисовых и центробежных сил и моментов и элементы c_i вектора гравитационных сил и моментов принимаются равными нулю. Т.е. модель динамики механической системы принимает следующий вид

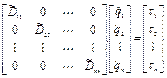,                                (2.52)

где 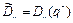, здесь 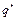- координаты точки позиционирования.

По существу модель динамики (2.51) сводится к системе двух интеграторов вида

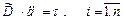.                               (2.53)

При синтезе управлений звеньями по модели (2.53) ошибка отработки задающих воздействий зависит от конфигурации механической системы и мы не в состоянии обеспечить независимость этих точностных характеристик в процессе движения манипулятора [21].

Подход Пола. В работе [21] Р. Полом был предложен подход к упрощению модели динамики (2.51), который предполагает сохранение диагональных элементов D_ii матрицы инерции D в функции обобщенных координат q, учет элементов c_i  вектора гравитационных сил и моментов c и обнуление всех элементов h_i вектора h. В этом случае модель динамики (2.51) принимает следующий вид:

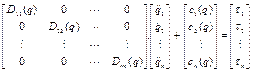.    (2.54)

Такой подход к упрощению динамической модели (2.51) дает более приемлемые результаты при синтезе регуляторов и реализации соответствующей системы управления.

Пример 2.3. Требуется упростить динамическую модель манипуляционного двухзвенника, полученную в примере 2.1, используя подход Пола.

Решение. В соответствие с уравнением (2.54), используя выражения, полученные в примере 2.1, имеем:

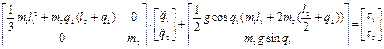.(2.55)

Линеаризация моделей динамики. Линеаризация динамических моделей манипуляционных роботов основывается на подходах, изложенных в работах [22, 23, 24].

Пусть уравнение

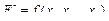                                     (2.56)

описывает динамическое или статическое поведение некоторого преобразователя, где 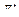- выходной сигнал этого преобразователя, а 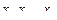могут представлять собой переменные состояния или входные сигналы системы. Функция  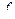многих переменных является нелинейной, дифференцируемой по своим аргументам и требуется ее линеаризовать в некоторой окрестности рабочей точки или сплайна вида (2.47) (в этом случае говорят о скользящей линеаризации). Тогда нелинейная функция (2.56) может быть аппроксимирована линеаризованной моделью вида

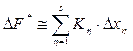,                            (2.57)

где 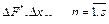 представляют собой малые отклонения в окрестности рабочей точки, а 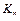называются коэффициентами линеаризации. Причем коэффициенты  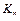являются элементами матрицы Якоби размерности ( ) вида

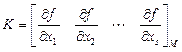,                           (2.58)

 вычисленной в рабочей точке 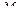. В случае линеаризации векторной функции f матрица K (2.58) будет иметь соответствующую размерность.

Пример 2.4. Требуется линеаризовать вектор 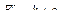, где 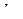- элементы динамической модели манипуляционного двухзвенника, полученные в примере 2.1, в окрестности точки позиционирования M с координатами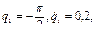 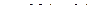. Приняты следующие значения параметров манипулятора (см. рис. 2.5): 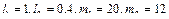. Сравнить результаты с упрощенной моделью (2.55).

Решение: Сформируем вектор :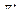

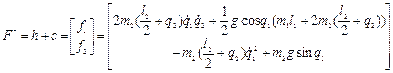.(2.59)

С учетом размерности вектора 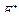 определим по выражению (2.58) матрицу K :

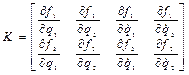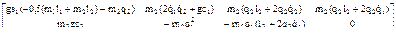= , (2.60)

где .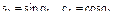

Подставим в полученную матрицу K значения координат рабочей точки M и массогабаритные параметры манипулятора:

.

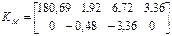Вычислим значения функции 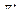в окрестности рабочей точки M :

.

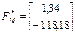Тогда, в силу выражения (2.57), функция 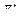(2.59) может быть аппроксимирована следующим выражением:

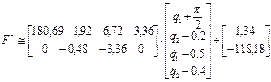.         (2.60,а)

Заменим в уравнении динамики манипуляционного двухзвенника сумму векторов h и c полученным аппроксимирующим выражением (2.59) и построим графики обобщенных моментов как для исходной модели (2.36), так и для упрощенной модели (2.55), используя интерполирующие полиномы (2.47)-(2.49) со следующими значениями коэффициентов:

(2.61)

Результаты моделирования представлены на рис. 2.8. Из графиков следует, что метод линеаризации дает приемлемые результаты в окрестностях целевой точки. Но подход Пола позволяет более адекватно описать динамику двухзвенника на всем интервале движения.

Естественно, представленные выводы корректны именно для рассматриваемой кинематической схемы двухзвенника. При данной схеме нам не пришлось пренебрегать недиагональными элементами матрицы инерции (поскольку они отсутствовали в исходной модели). Кроме того, подход Пола предполагает расчет динамических коэффициентов на всем интервале движения звеньев манипулятора. Можно предположить, что вычисление матрицы K (2.60) вдоль полинома (2.47)-(2.49), (2.61), а не только в окрестности рабочей точки M, позволит более корректно аппроксимировать динамику двухзвенника на всем интервале движения.

Следует подчеркнуть, что на быстрых траекториях, отброшенные элементы уравнений динамики могут составлять до 30% от общей динамики робота, что может привести не только к существенному уменьшению качества отработки спланированных траекторий, но даже и к потере их устойчивости [18].