Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Решение кинематических задач, описывающих движение манипуляционных роботов без учета сил и моментов, вызвавших это движение, было представлено в предыдущем разделе. Предметом же динамики манипуляторов, как раздела робототехники, является математическое описание действующих на манипулятор сил и моментов в форме уравнений динамики движения, описывающих взаимосвязь между силами и моментами, действующими в сочленениях, с одной стороны, и скоростями, ускорениями, координатами и параметрами робота с другой стороны. Такие уравнения необходимы для моделирования движения манипулятора, при выборе законов управления и при оценке качества кинематической схемы и конструкции манипулятора.

В зависимости от свойств тел, движение которых изучается, характера изучаемых движений и содержания вопросов, на которые должен быть получен ответ, механика, как известно [13], делится: на механику точки и механику системы точек; механику твердого (недеформированного) тела и системы твердых тел; механику упругих тел (систему тел). Вообще – то, говоря, в природе не существует ни материальных точек, ни твердых (недеформируемых) тел, ни абсолютно упругих тел. Все это абстракции, которыми приходится пользоваться для того, чтобы правильно отразить основные качественные свойства исследуемых объектов, при этом значительно упростив процесс исследования. В некоторых случаях размеры и форма движущихся тел не играют существенной роли, и тогда тело можно принять за материальную точку. Однако в целом ряде случаев это оказывается невозможным, так как именно размеры и форма тел определяют характер интересующего нас движения. Если при этом тело является настолько жестким, что его деформациями, возникающими при рассматриваемых движениях, можно пренебречь, то упругие свойства тела не играют роли. Тогда тело можно рассматривать как недеформируемое, или как абсолютно твердое. Тогда для определения положения тела достаточно знать положения любых трех точек этого тела, не лежащих на одной прямой, иначе говоря, задать положение произвольного недеформирующегося треугольника, жестко связанного с телом. Для определения положения одной точки в пространстве нужно знать три её координаты. Определение положения трех произвольных точек в пространстве требует задания девяти величин-координат трех точек. Однако в жестком треугольнике неизменяющиеся расстояния между каждой парой точек выражаются определенным образом через координаты точек. Девять координат вершин треугольника зависимы, т. е. связаны между собой тремя уравнениями. Поэтому чтобы определить положение твердого тела в пространстве, нужно задать только шесть независимых величин [13].

53

Если тело способно деформироваться, то положение нескольких его точек уже не определяет положения всех остальных его точек и положение каждой точки тела должно быть задано независимо. Поскольку всякое реальное тело в действительности способно деформироваться, оно должно было бы обладать бесконечным числом степеней свободы. Только пренебрегая деформациями тела, считая его абсолютно жестким (твердым), можно говорить о конечном числе его степеней свободы (не превышающем шести). Реальный механизм, как правило, отличается от механизма с идеальной схемой. Прежде всего, звенья могут быть деформируемыми и перемещения их отдельных точек в движении могут отличаться от перемещения твердого тела [14]. Шарниры механизма не могут быть выполнены в точности так, чтобы они обеспечивали абсолютное прилегание звеньев. Наличие трения в кинематических парах изменяет схему передачи сил в механизме. К этому следует прибавить и то обстоятельство, что такое взаимодействие звеньев как деталей при трении приводит к износу, изменяющему со временем их форму и условия сопряжения, вследствие чего реальные условия все больше и больше отклоняют его от идеального. Однако замена реального механизма идеальной расчетной схемой возможна при условии, что отклонения, вызванные условиями реального механизма, несущественны. В этом разделе механическая система манипуляторов будет описана с помощью идеализированной схемы, в которой звенья предполагаются абсолютно твердыми, связи - идеальными [13].

Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновой или лагранжевой механики. Результатом применения этих законов являются уравнения, связывающие действующие в сочленениях силы и моменты с кинематическим характеристиками и параметрами движения звеньев. Уравнения динамики движения реального манипулятора могут быть получены традиционными методами Лагранжа – Эйлера или Ньютона – Эйлера или с применением обобщенных уравнений Д’Аламбера. Все эти уравнения различны по форме, поскольку были получены для разных целей. Некоторые из них обеспечивают минимальное время вычисления управляющих моментов в сочленениях манипулятора, другие используются при синтезе и анализе законов управления, третьи применяются для моделирования движения манипулятора с помощью ЭВМ [3]. Но они эквивалентны в том смысле, что описывают динамику движения одной и той же физической системы.

Вывод уравнений динамики движения манипулятора методом Лагранжа – Эйлера наиболее формализуем, и отличается простотой и единством подхода. В рамках предположения о том, что звенья представляют собой твердые тела, этот подход приводит к системе нелинейных дифференциальных уравнений второго порядка. Получаемые уравнения динамики движения манипуляторов, в общем случае, существенно нелинейны и отражают эффекты, связанные с действием сил инерции, обусловленных ускоренным движением звеньев, действием кориолисовых и центробежных сил, а также действием силы тяжести. Более того, действующие в сочленениях силы и моменты зависят от параметров манипулятора, мгновенных значений обобщенных координат, скоростей и ускорений, а также перемещаемого манипулятором груза. Уравнения Лагранжа – Эйлера обеспечивают строгое описание динамики манипулятора и могут быть использованы для разработки усовершенствованных законов управления в пространстве обобщенных координат. В меньшей степени они используются для решения прямой и обратной задачи динамики. Прямая задача динамики состоит в том, чтобы по заданным силам и моментам определить обобщенные ускорения, интегрирование которых позволяет получить значения обобщенных координат и скоростей. Обратная задача динамики заключается в том, чтобы по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты. Для решения обеих названных задач, как правило, необходимо вычислять динамические коэффициенты 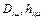 и .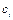

С целью получения более эффективных с вычислительной точки зрения алгоритмов расчета обобщенных сил и моментов некоторые исследователи использовали уравнения Ньютона – Эйлера [3]. Вывод уравнений движения манипулятора методом Ньютона – Эйлера прост по содержанию, но весьма трудоемок. Результатом является система прямых и обратных рекуррентных уравнений, последовательно применяемых к звеньям манипулятора. С помощью прямых уравнений последовательно, от основания к конечному звену, вычисляются кинематические характеристики движения звеньев, такие, как линейные и угловые скорости и ускорения, линейные ускорения центров масс звеньев. Обратные уравнения позволяют последовательно, от конечного звена к основанию, вычислить силы и моменты, действующие на каждое из звеньев. Наиболее важный результат такого подхода состоит в том, что время, необходимое для вычисления обобщенных сил и моментов, прямо пропорционально числу сочленений, но не зависит от реализующейся в процессе движения конфигурации манипулятора. Это позволяет реализовать простые законы управления манипулятором в реальном времени.

Для синтеза законов управления желательно иметь в распоряжении замкнутую систему дифференциальных уравнений, точно описывающую динамику движения манипулятора. Кроме того, желательно, чтобы в этих уравнениях можно было легко выделить составляющие, отражающие действие сил различной природы с тем, чтобы выбором закона управления обеспечить их максимальную компенсацию .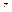

Еще один подход к формированию эффективной в вычислительном плане системы точных уравнений движения основан на применении принципа Д’Аламбера. Этот подход позволяет получить уравнения движения в векторно-матричной форме, удобной для анализа. Помимо того, что эти уравнения обеспечивают снижение по сравнению с уравнениями Лагранжа – Эйлера вычислительных затрат на расчет динамических коэффициентов, они позволяют различать динамические эффекты, обусловленные вращательным и поступательным движением звеньев, что весьма полезно при синтезе управления в пространстве состояний. Вычислительная эффективность этих уравнений обусловлена использованием для описания кинематики звеньев матриц поворотов и векторов относительного положения [3].

Затраты на вычисление обобщенных сил и моментов с применением обобщенных уравнений Д’Аламбера имеют порядок O ( n ³ ), с применением уравнений Лагранжа – Эйлера – порядок O ( n ⁴ ) (при оптимизации - O ( n ³ )), с применением уравнений Ньютона – Эйлера - O(n), где n – число степеней свободы манипулятора [3].

В этом разделе уравнения движения манипулятора будут получены методом Лагранжа – Эйлера, как наиболее формализуемого и использующего промежуточные результаты решения задач кинематики, рассмотренных в предыдущем разделе.