Достаточно широкий круг задач управления манипуляционными роботами предполагает представление уравнений динамики не в фазовом пространстве 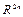обобщенных координат, как это мы рассматривали в предыдущих параграфах, а в фазовом пространстве  внешних (рабочих) координат. В первую очередь это относится к задачам управления манипуляционными роботами, осуществляющими силовое взаимодействие с внешней средой [17]. 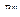Кроме того, структура системы управления манипуляционным роботом предполагает перевод узловых точек, формируемых аппроксимирующим устройством, из рабочего пространства в пространство обобщенных координат 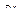. Эта процедура требует обязательного, в общем случае, неформализуемого решения обратной задачи кинематики (1.2), с последующим формированием интерполирующих полиномов и их подачей, в качестве задающего воздействия, на приводы манипуляционного робота. В работе [25] предлагаются процедуры синтеза таких регуляторов, которые позволяют исключить блок решения обратной задачи кинематики и интерполяторы из структуры систем управления манипуляторами, но требуют представления моделей их динамики в фазовом пространстве  внешних (рабочих) координат.

Пусть модель динамики манипуляционного робота представлена в виде (2.65). На основе этой модели требуется описать динамику рабочего органа манипулятора в фазовом пространстве  внешних (рабочих) координат.

Исходя из баланса мощностей, запишем следующее соотношение [17]:

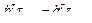,                                          (2.72)

где 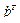- транспонированный вектор внешних скоростей (скоростей рабочего органа манипулятора), 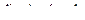, , 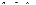здесь 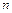- число степеней подвижности манипулятора;

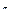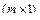- - вектор внешних сил и моментов сил, действующих на рабочий орган манипулятора. Компоненты этого вектора могут измеряться и тогда ;

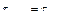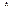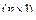- -вектор обобщенных скоростей, 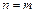, т.е. мы предполагаем, что манипулятор является кинематически безызбыточным;

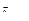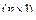- -вектор внутренних сил и моментов. Под этими силами (моментами сил) мы будем понимать все силы (моменты), действующие в сочленениях робота.

Предположим, что мы определили решение прямой задачи кинематики вида (1.37), на основе которого связь между внешними скоростями 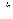 и ускорениями 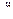, с одной стороны, и обобщенными координатами 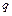, скоростями  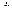и ускорениями 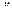, с другой стороны, может быть выражена следующими соотношениями:

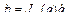,                                                  (2.73)

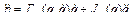,                            (2.73, а)

где 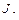- - матрица Якоби решения прямой задачи кинематики (1.37), ;

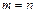- -матрица, элементы которой определяются дифференцированием по времени элементов матрицы .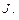

Подставив в уравнение (2.72) выражение (2.73), получим:

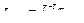,                                            (2.74)

где 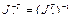- матрица, обратная транспонированной матрице Якоби .

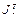Таким образом, для того, чтобы трансформировать уравнения динамики (2.65) из фазового пространства 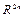обобщенных координат в фазовое пространство координат внешних, необходимо умножить слева все элементы уравнения (2.65) на оператор перехода 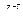. В результате, с учетом передаточных механизмов, получим:

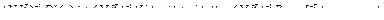. (2.75)

Выразим теперь вектор обобщенных ускорений 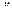 из выражения (2.73, а) и подставим его в уравнение (2.75). С учетом равенств (2.73) и (2.68) получим:

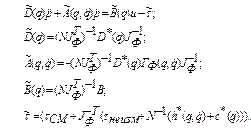                                     (2.76)

Подстановкой решения обратной задачи кинематики (1.2) в уравнения (2.76) можно получить их зависимость только от внешних координат 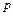 и скоростей  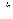вида

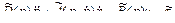.                              (2.77)

Уравнения (2.77) описывают динамику рабочего органа манипуляционного робота в фазовом пространстве 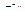 внешних координат.

Когда управляемыми и измеряемыми являются только обобщенные координаты 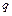  и скорости 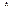, то представление динамики в виде уравнений (2.77) хотя и возможно, но не всегда представляется целесообразным, тогда боле предпочтительными являются уравнения (2.76).

Пример 2.6. Требуется представить в фазовом пространстве 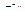 внешних координат математическую модель инерционных сил  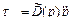механической системы двухзвенника, представленного на рис. 1.10, используя результаты примеров 1.9 и 2.1 и принимая .

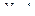Решение.

В соответствие с решением прямой задачи кинематики для рассматриваемого двузвенника

,

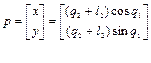запишем матрицу Якоби 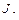, используя выражение (1.40). В результате имеем

.

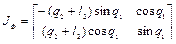Вычислим 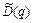как

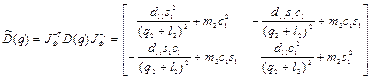, (2.78)

.

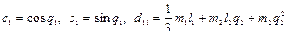С учетом решения обратной задачи кинематики (1.44), (1.45), полученной для рассматриваемого двухзвенника в п.1.9.1, запишем инерционные силы 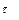в функции внешних координат 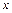и :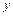

;

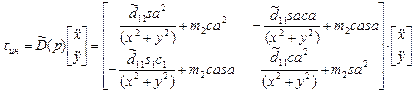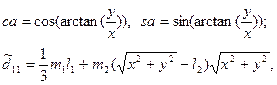
здесь 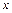, 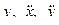- соответственно текущие значения координат положения и ускорений рабочего органа двухзвенника в пространстве внешних координат, которые могут быть определены через решение прямой задачи кинематики (в функции обобщенных координат) или же посредством внешних сенсорных элементов и дополнительных блоков вычисления производных.