Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Выражения для определения кинематической энергии звеньев манипулятора и механической системы в целом. Понятие матрицы инерции массы звена и ее определение

Рассмотрим кинематическую схему произвольного манипулятора, представленную на рис. 2.1, и определим кинетическую энергию 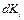 элемента массой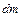 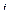-го звена так:

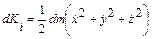           .                         (2.15)

Пусть заданы векторы 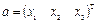и 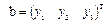, введем произведение такое, что .

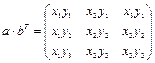Тогда скалярное произведение 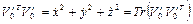 и выражение (2.15) можно записать в виде

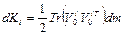,                               (2.16)

здесь 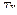 - след соответствующей матрицы, т.е. сумма ее диагональных элементов.

С учетом выражения (2.8) выражение (2.16) может быть представлено в виде

.

 

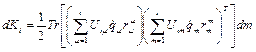Раскроем скобки под знаком транспонирования:

65

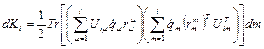.    (2.17)

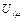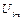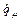Поскольку  и , и 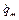 не являются функциями 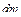, то выражение (2.17) можно записать в следующей форме:

.

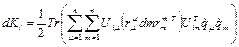Тогда кинетическая энергия 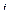-го звена может быть определена посредством следующего выражения:

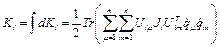,   ………(2.18)

где 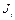- матрица инерции массы звена –

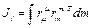.                                     (2.19)

Кинетическая энергия всей системы будет определяться выражением [3]:

.

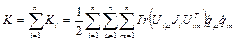К вопросу определения матрицы инерции массы звена

Предположим, что координаты центра тяжести 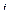-го звена в 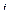-й системе координат заданы вектором в однородных координатах 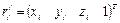. Тогда общий вид матрицы  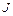будет следующий [3]:  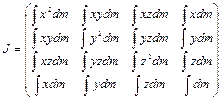               .. (2.20)

Общий вид матрицы (2.20) не эффективен при расчете уравнений динамики, поэтому принимают упрощающие предположения. Представим звенья манипулятора стержнями или цилиндрами, продольные оси которых совпадают с одной из осей связанной системы координат.

Если 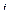- е звено является поступательным, то матрица инерции такого звена имеет вид

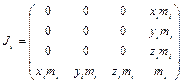                                (2.21)

где 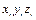 - координаты центра тяжести 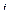- го звена в 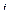- й системе координат, а  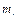- масса 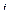- го звена.

Для вращающихся звеньев принимаются равные нулю центробежные (недиагональные) моменты инерции, а из моментов инерции относительно центральных осей (диагональных) остается только тот, который соответствует продольной оси звена. Т. е. матрица инерции массы 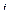-го звена принимает вид

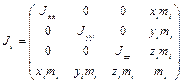                                (2.22)

Если звено представляем стержнем, показанным на рис. 2.3, а,

б

а

                    

 

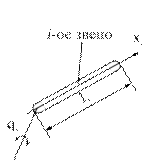
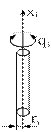
Рис. 2.3. К вопросу определения момента инерции массы - го звена

 

то 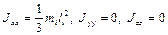. Если же с продольной осью совпадает ось 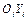, то 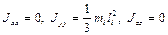, здесь  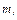- масса,  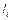- длина 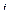- го звена. Аналогичным образом формируется матрица инерции массы 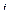-го звена и для случая, когда с продольной осью 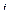-го звена совпадает ось 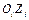. Если звено представляем     цилиндром, как показано на рис 2.3, б, то для этого случая 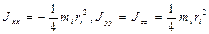, здесь  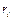─ радиус  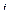- го звена. Опять же, если, например, ось вращения звена совпадает с осью  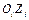системы координат 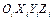, жестко связанной с 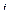-м звеном, то 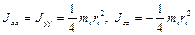. Для случая, когда с осью вращения совпадает ось , .

67

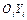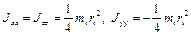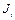Отметим, что величины  (i=1, 2,…,n) зависят только от распределения массы i-го звена в i-й системе координат и не зависят ни от положения, ни от скорости звеньев. Это позволяет, однажды вычислив матрицы 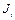, использовать полученные значения в дальнейшем для вычисления кинетической энергии манипулятора.