Для некоторых простейших форм кинематических цепей удается получить решение ОЗК в аналитическом виде непосредственно из решения ПЗК.

 Пусть задан манипуляционный двухзвенник, рассмотренный в примере 1.6. Для него известно решение ПЗК, полученное в п. 1.6.3, вида

.

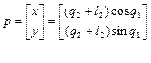Возведем в квадрат каждый из элементов вектора p и суммируем полученные выражения. Получим:

.

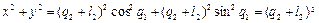Из последнего равенства имеем

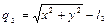.                                  (1.44)

Теперь разделим второй элемент вектора p на его первый элемент. Получим: 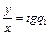. Отсюда

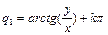, k =0,1,2…                                 (1.45)

Выражения (1.44) и (1.45) образуют решение ОЗК для рассмотренного двухзвенника. Подставляя в них требуемые координаты x ₀ и y ₀ точек позиционирования характеристической точки МР (в данном случае это точка O ₂, см. рис. 1.10), мы можем определить соответствующие им значения обобщенных координат q ₁ и q₂.

Геометрический подход к решению ОЗК

Геометрический подход является одним из самых распространенных при решении ОЗК для кинематических схем различной сложности. Получение функциональных зависимостей вида (1.43) осуществляется исходя из геометрических построений для каждой конкретной кинематической схемы. В частности, решение ОЗК для шестизвенного манипуляционного робота типа Puma с использованием геометрического подхода приведено в работе [3].

Пусть требуется решить ОЗК для трехзвенного робота, рассмотренного в п.1.7, кинематическая схема которого представлена на рис. 1.14. Пусть также заданы координаты схвата в базовой, неподвижной системе координат O₀X₀Y₀Z₀, принимающие текущие значения x_cx, y_cx, z_cx. В соответствии с поставленной задачей требуется получить зависимости q ₁ = f ₁ ( x_cx , y_cx , z_cx ), q ₂ = f ₂ ( x_cx , y_cx , z_cx ), q ₃ = f ₃ ( x_cx , y_cx , z_cx ).

Из рис. 1.14 очевидно следующее равенство:

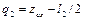.                                            (1.46)

Для определения зависимостей q ₁ = f ₁ ( x_cx , y_cx , z_cx ), q ₃ = f ₃ ( x_cx , y_cx , z_cx ) произведем геометрические построения на плоскости O₀X₀Y₀ так, как

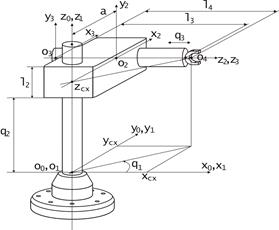
Рис. 1.14. К решению ОЗК для манипуляционного трехзвенника

показано на рис. 1.15, где 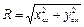. Поскольку отрезок O ₄ M = l ₄ - q ₃, то из треугольника O ₀ MO ₄ находим, что

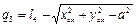,                            (1.47)

где a, l₄- конструктивные параметры.

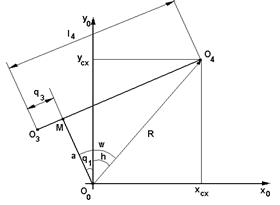
Рис. 1.15. Геометрические построения на плоскости для трехзвенного МР

Из рис. 1.15 также очевидны равенства q₁=w-h, w=90^o-arcsin(a/R), tgh= (x_cx/y_cx). Отсюда имеем:

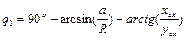.                          (1.48)

Выражения (1.46)-(1.48) и являются решением ОЗК для представленного МР. Подставляя в них желаемые значения внешних координат схвата x_cx, y_cx, z_cx, задаваемых в неподвижной системе координат O₀X₀Y₀Z₀, мы можем определить соответствующие им значения обобщенных координат q_i, которые используются для формирования программы движения соответствующего привода.