В п. 1.6 мы получили решение прямой задачи кинематики, которое является оператором перехода из пространств Rⁿ обобщенных координат в пространство R^m координат внешних. Т.е. решение ПЗК, определенное выражением (1.37), устанавливает зависимость элементов вектора p внешних (базовых, рабочих) координат рабочего органа МР (или какой − то его характеристической точки) в функции вектора q обобщенных координат. А как связаны внешние 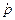и обобщенные  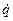скорости? Как влияет приращение обобщенных координат на приращение внешних координат? И наоборот, как изменение скоростей внешних влияет на изменение скоростей обобщенных? Чтобы ответить на эти вопросы, продифференцируем по времени решение ПЗК (1.37): 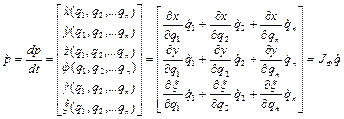, (1.39)

где 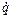- (nx1)- вектор обобщенных скоростей; J _Ф – в общем случае ( 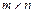)-матрица, называемая матрицей Якоби (или якобианом [3], что математически некорректно) манипулятора. Причем

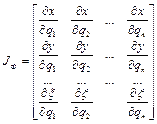.                                 (1.40)

Матрица Якоби манипулятора (1.40) и есть оператор перехода из пространства Rⁿ обобщенных скоростей в пространство R^m внешних скоростей.

Если m=n, то существует определитель

D = det J _Ф                                         (1.41)

называемый якобианом матрицы (1.40).

Если 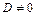, то существует матрица J _Ф ^-1, обратная матрице J _Ф, и справедливо равенство:

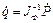.                                       (1.42)

Равенство (1.42) является оператором перехода из пространства R^m внешних скоростей в пространство Rⁿ обобщенных скоростей.

Если же при каких - то значениях q = q_d , D ( q_d )=0, то эти значения обобщенных координат соответствуют вырожденным конфигурациям МР. Или говорят, что выражения (1.37), в точках q = q_d, недостаточно для описания перехода из пространства Rⁿ обобщенных координат в пространство R^m внешних координат и оно должно быть дополнено картами, снимающими некорректность решения ПЗК в этих точках [5]. 

Матрица Якоби манипулятора (1.40) может быть использована для формирования управляющих воздействий по алгоритмам, предполагающим задание траекторий движения в пространствах внешних координат и внешних скоростей [6]. В этих случаях необходимо использовать процедуры обхода вырожденных конфигураций таких, например, как изложено в работе [7].

Следует отметить, что при переходе от производных по времени к приращениям координат, выражение (1.39) может быть использовано для анализа точности позиционирования характеристической точки рабочего органа МР в зависимости от погрешностей, определяемых неточностью изготовления элементов механической системы МР, погрешностью измерения обобщенных координат и т.д. [8].

 Кроме того, промежуточные результаты решения ПЗК в виде матриц  используются для вывода уравнений динамики МР.

Пример 1.11. Определить матрицу Якоби и вырожденные конфигурации манипуляционного робота, рассмотренного в параграфе 1.7, если обобщенные координаты изменяются в следующих диапазонах: q₁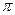=[-0,9 , 0,9 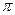], q₂=[0,1], q₃=[0, 0,3], здесь, а l₄=0,5 [м], l₂=0,1[м], a=0,5[м].

Решение. В соответствии с решением ПЗК (1.37) и выражением для определения матрицы Якоби (1.40) получим:

.

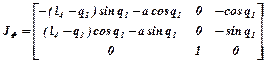Соответственно, якобиан манипулятора определяется выражением:

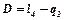
и при заданных значениях обобщенных координат МР не имеет вырожденных конфигураций.