Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Итак, в предыдущем пункте мы получили параметры звеньев, свели их в табл. 1. Теперь, подставив эти параметры в матрицу преобразований Денавита-Хартенберга (1.33), мы можем получить матрицы однородных преобразований: 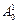, описывающую положение и ориентацию системы координат 1-го звена относительно базовой 0-й системы; 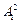, описывающую положение и ориентацию системы координат, жестко связанной со 2-м звеном, в системе координат 1-го звена и так далее, вплоть до матрицы 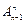, которая описывает положение и ориентацию n-й системы координат, связанной с последним n-м звеном, где и закреплен рабочий орган МР в системе координат (n-1)-го звена. Рассмотрим пример получения этих матриц на основе данных, приведенных в табл. 2.

Пример 1.8. Для манипуляционного двухзвенника, рассмотренного в примерах 1.6 и 1.7, требуется получить матрицы однородных преобразований, отражающие связь между системами координат двух соседних звеньев (естественно, включая неподвижное, нулевое звено).

Решение. Подставим параметры 1-го звена из первой строки табл. 2 в матрицу преобразований Денавита-Хартенберга (1.33). Получим матрицу однородных преобразований системы координат 1-го звена в системе координат 0-го , неподвижного звена:

.

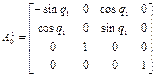Аналогичным образом, подставляя параметры 2-го звена в матрицу (1.33), имеем:

.

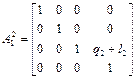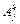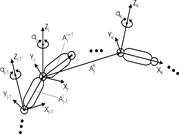
 Как уже было отмечено выше, полученные матрицы отражают связь только между соседними звеньями. А как получить матрицу преобразований, описывающую систему координат некоторого k-го звена относительно системы координат некоторого j-го звена, при j<k, т.е. матрицу ? Естественно, мы предполагаем, что нам известны матрицы 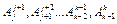, построенные с использованием параметров из табл. 1. Возможны два варианта рассуждений, позволяющие получить искомое решение. Первый из них основан на правиле «последовательных преобразований» [3] и продемонстрирован на рис. 1.11, а.

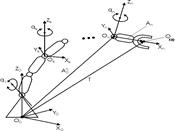а …….  б

                                                                          

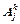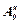Рис. 1.11. Преобразования систем координат: а - ; б - и T

Из рисунка следует, что для получения преобразования 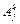 необходимо последовательно перемножить матрицы преобразований, соответствующие векторам, сумма которых является вектором 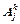. В соответствии с этим правилом имеем

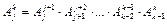.                    (1.34)

36

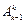Второй вариант рассуждений основывается на рассмотренных нами в п.1.4.3 правилах получения матрицы композиции однородных преобразований. Будем считать k-ю систему координат подвижной, а (k -1)-ю – неподвижной. Матрица  есть матрица однородных преобразований для этих систем. Теперь за подвижную примем (k -1)-ю систему координат, а (k -2)-ю − за неподвижную. Очевидно, что в соответствии с правилом 2, изложенным в п. 1.4.3, предыдущий результат, т.е. матрицу 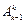, мы должны слева доумножить на матрицу 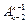. Последовательно выполняя композицию преобразований j-й системы координат к k-й системе, мы также получим выражение (1.34).

Теперь очевидно, что для получения матрицы однородных преобразований n-й системы координат, жестко связанной с n-м, конечным звеном (см. рис. 1.11,б) в базовую систему координат, связанную с неподвижным, нулевым звеном манипуляционного робота, необходимо использовать следующее выражение, аналогичное выражению (1.34):

.                        (1.35)

Матрица (1.35) определяет положение n-й системы координат и ориентацию ее осей относительно базовой системы координат. Предположим, что центр n-й системы координат, построенной в соответствии с правилами, изложенными выше, не совпадает с рабочим органом манипулятора или какой − то его характеристической точкой O_хар (рабочая кромка резца, выходное отверстие краскопульта и т.п.). И что эта точка в n-й системе координат описывается матрицей однородных преобразований A_n вида

,

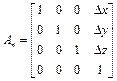где 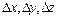- координаты характеристической точки рабочего органа манипулятора в n-й системе координат.

Тогда матрица T, определяемая выражением

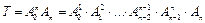                   (1.36)

называется матрицей манипулятора. Именно эта матрица несет информацию об ориентации и положении рабочего органа МР в базовой системе координат как функции обобщенных координат q_i , i= 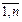, здесь n-число звеньев.

Следует отметить, что если центр n-й системы координат совпадает с характеристической точкой рабочего органа МР, то матрица A_n является единичной и, соответственно, матрица манипулятора определяется выражением (1.35).

В матрице манипулятора T и в матрицах 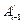подматрицы направляющих косинусов R _{3 x 3} из выражения (1.22) сохраняют все свойства, изложенные в п. 3.4, что может быть использовано для проверки корректности их определения.

Пример 1.9. Определить матрицу манипулятора для манипуляционного двухзвенника, рассмотренного в примере 1.6, если характеристическая точка его рабочего органа совпадает с центром системы координат O₂X₂Y₂Z₂.

Решение. В соответствии с условиями задачи используем выражение (1.35) и результаты примера 1.9. Получим:

,

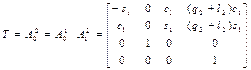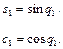
Решение ПЗК

Теперь отметим наиболее важный момент в разделе кинематики манипуляционных роботов: решение прямой задачи кинематики (1.1) определяется наддиагональными элементами матрицы манипулятора T .

То есть решение ПЗК в общем случае имеет вид

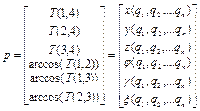,                      (1.37)

где x , y , z - координаты положения характерной точки рабочего органа МР; φ, γ, ξ- углы ориентации системы координат, жестко связанной с рабочим органом МР в базовой, неподвижной системе координат.

Решение ПЗК, представленное векторами (1.1) и (1.37), имеет размерность (mx1). Поскольку мы рассматриваем кинематически безызбыточные манипуляторы, т.е. когда m=n, с кинематическими парами пятого класса, то размерность вектора решения ПЗК определяется количеством звеньев кинематической цепи. Так, для матрицы манипулятора, полученной в примере 1.9, решение прямой задачи кинематики имеет вид

,

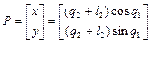где x, y- координаты точки O₂ в базовой системе координат.

Если же пространственный манипулятор имеет три звена, то решением ПЗК являются элементы T(1,4), T(2,4), T(3,4) матрицы манипулятора T.

38

Если же плоский МР имеет три звена, то для кинематически безызбыточной задачи в качестве решения ПЗК мы выбираем два ненулевых элемента вектора p _3х1 (см. обозначения к матрице (1.22)) из матрицы манипулятора и наддиагональный элемент подматрицы R _{3 x 3} матрицы манипулятора, являющийся функцией обобщенных координат.

38

Если же у пространственного манипулятора звеньев больше трех, то мы можем уже определенным образом, если это требуется, ориентировать рабочий орган манипулятора, а не только перемещать его в пространстве базовых координат. В этом случае, в решение ПЗК, помимо всех элементов вектора p _3х1, дополнительно включается соответствующее число независимых, наддиагональных элементов подматрицы R _{3 x 3} матрицы манипулятора, также являющихся функциями обобщенных координат.

Следует отметить еще раз, что размерность вектора 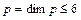. Это означает, что даже при числе звеньев механической системы неплоского манипулятора n>6, т.е. при кинематической избыточности МР размерность вектора p не может быть больше шести.

 

1.7. Решение ПЗК на примере манипуляционного трехзвенника

 

В качестве примера рассмотрим манипуляционный робот (МР) с цилиндрической системой координат и состоящий из трех звеньев. Общий вид МР и направление осей вращения в сочленениях представлены на рис. 1.12, где q ₁ , q ₂ , q ₃ – обобщенные координаты. Такой МР может применяться для выполнения многообразных операций – сборки, монтажа, сортировки, упаковки, погрузки − разгрузки и т. д.

1. Построим связанные системы координат в соответствии с правилами, изложенными в п. 1.6.1 (см. рис. 1.12). Здесь 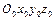- базовая (связанная с неподвижным основанием) система координат;  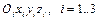- системы координат, жестко связанные с i-ми звеньями.

2.   В соответствии с п. 1.6.2 и рис. 1.12 заполним табл. 3 параметров МР.

Таблица 3

Параметры звеньев трехзвенника             

Звено	d	a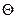
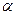
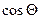
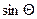
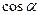
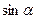
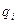
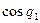
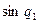
1	0	0		0			1	0
2	q2+0,5l2	-a	0,5π	0,5π	0	1	0	1
3		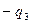0	0	0	1	0	1	0

 

3. Для каждой кинематической пары, используя преобразование Денавита-Хартенберга (1.33), получим матрицы однородных преобразований систем координат:

 

; ;

.

 

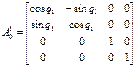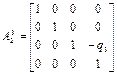4. Примем точку O₄ за характеристическую точку схвата и вычислим матрицу манипулятора как произведение матриц:

 

= ,

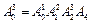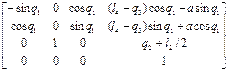где 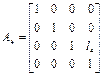, здесь l ₄ - аппликата точки O₄ в системе координат третьего звена.

 

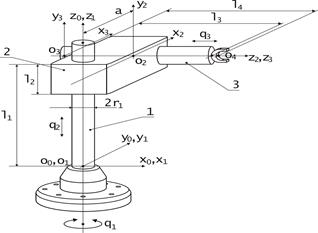
Рис. 1.12. Трехзвенный манипулятор

 

В соответствии с п. 1.6.4 решение ПЗК для представленного манипулятора имеет вид:

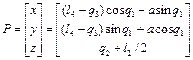.                      (1.38)

Для самопроверки можно подставить фиксированные значения обобщенных координат в решение ПЗК и сравнить значения базовых координат схвата с получаемыми из геометрических соображений по рис. 1.13.

Рис. 1.13. Рабочая зона МР с цилиндрической системой координат