Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотренные матрицы поворота определяют положение осей связанной (подвижной) системы координат относительно осей абсолютной (неподвижной) системы. В соответствии с выражением (1.11) операция обращения матриц поворота совпадает с операцией их транспонирования. Это означает, что вектор-строки матриц поворота задают направления осей абсолютной системы координат OXYZ в связанной системе координат OUVW. Такая геометрическая интерпретация матриц поворота позволяет эффективно решать многие задачи кинематики манипуляторов и сформулировать следующие полезные свойства матриц поворота:

1. Каждый столбец матрицы поворота представляет собой единичный вектор в направлении соответствующей оси связанной системы координат OUVW, заданный своими координатами в абсолютной системе координат OXYZ. Каждая строка матрицы поворота представляет собой единичный вектор в направлении соответствующей оси абсолютной системы координат OXYZ, заданный своими координатами в связанной системе OUVW.

2. Поскольку каждый столбец и каждая строка матрицы поворота представляют собой координаты единичного вектора, то длина векторов, определяемых строками и столбцами матрицы поворота, равна 1.

3. Для правосторонней системы координат определитель матрицы поворота равен +1, для левосторонней системы он равен –1. Напомним, что у правосторонней системы координат поворот оси OY к оси OX, если смотреть с положительного направления оси OZ, осуществляется по часовой стрелке.

4. Скалярное произведение векторов, определяемых двумя различными столбцами (строками), равно нулю.

5. Операция обращения матрицы поворота совпадает с операцией ее транспонирования.

Приведенные свойства полезны при проверке правильности записи или перемножения матриц поворота и будут использованы в последующем при рассмотрении матриц однородных преобразований.

 

1.4. Матрицы однородных преобразований

Понятие однородных координат и матрицы однородных преобразований. Матрицы комбинаций однородных преобразований и их геометрический смысл

1.4.1. Однородные координаты и матрицы однородных преобразований

В предыдущем параграфе мы рассмотрели матрицы поворотов, содержащие полную информацию о взаимной ориентации осей двух систем координат. Но матрица поворота размерности (3х3) не несёт информации о расположении центра связанной системы координат в абсолютной системе. Как, впрочем, она и не несет информации о положении центра абсолютной системы координат в связанной системе. Указанное обстоятельство определило необходимость привлечения дополнительного матричного аппарата в виде матриц однородных преобразований размерности 4х4 для описания не только взаимной ориентации осей двух систем координат, но и взаимного положения их центров. Необходимость учета взаимного расположения двух систем координат определяется наличием поступательных, а не только вращательных перемещений звеньев кинематических цепей МР. Построение матриц однородных преобразований стало возможным при введении понятия однородных координат.

В общем случае изображение n-мерного вектора вектором размерностью n +1 называется представлением в однородных координатах. При таком представлении преобразование n-мерного вектора производится в n +1-мерном пространстве, а физический n-мерный вектор получается делением однородных координат на ( n +1)-ю компоненту s. Так, вектор p = (p_x, p_y, p_z)^T положения в трёхмерном пространстве в однородных координатах представляется расширенным вектором 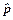=(s p_x, s p_y, s p_z, s) ^T. Физические координаты связаны с однородными следующим образом:

.

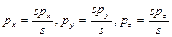Однородная матрица преобразования представляет собой матрицу размерностью 4х4, которая преобразует вектор, выраженный в однородных координатах, из одной системы координат в другую. Однородная матрица преобразования может быть разбита на 4 подматрицы [3]:

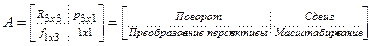  (1.22)

Верхняя левая подматрица размерностью 3х3 представляет собой рассмотренную выше матрицу поворота. Ее еще называют матрицей направляющих косинусов; верхняя правая подматрица размерностью 3х1 представляет собой вектор положения начала координат связанной (подвижной) системы координат в абсолютной (неподвижной); нижняя левая подматрица размерностью 1х3 задает преобразование перспективы; 4-й диагональный элемент является глобальным масштабирующим множителем.

Если вектор p трехмерного пространства выражен в однородных координатах и s=1 (т.е. 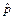= (p_x, p_y, p _z ,,1 )^T), то, используя понятие матрицы преобразования, можно сформировать однородную матрицу преобразования поворота А _{ось, угол}, задающую преобразование поворота и имеющую размерность 4х4. Однородная матрица поворота получается соответствующим расширением обычной матрицы поворота R, имеющей размерность 3х3. Так, однородное представление для матриц (1.14) и (1.15) имеет следующий вид:

 

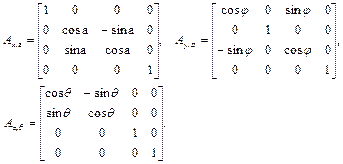  (1.23)

Эти матрицы размерностью 4х4 называются матрицами однородных элементарных поворотов.

Верхняя правая подматрица матрицы однородных преобразований, имеющая размерность 3х1, определяет положение центра связанной системы координат в абсолютной системе, т.е. задает параллельный перенос системы координат OUVW относительно абсолютной системы OXYZ на вектор (dx, dy, dz)^T :

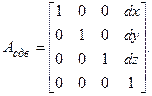                               (1.24)

 Матрица (1.24), размерности 4х4, называется матрицей однородного элементарного сдвига.

Левая нижняя подматрица матрицы однородных преобразований размерностью 1х3 определяет преобразование перспективы, используемое в задачах машинного зрения и при калибровке изображений. В задачах кинематики МР эта вектор-строка имеет нулевые элементы. В дальнейшем будем полагать, что элементы этой подматрицы нулевые, что соответствует нулевому преобразованию перспективы.

Диагональные элементы однородной матрицы преобразования определяют локальное и глобальное изменения масштаба. Первые три диагональных элемента задают локальное растяжение/сжатие, или изменение масштаба:

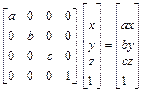                          (1.25)

Очевидно, что значения координат претерпевают изменение масштаба, определяемое соответственно скалярами a, b, c. Заметим, что матрицы элементарных поворотов А_{ось, угол} не дают эффекта локального изменения масштаба.

Рассмотрим влияние 4-го диагонального элемента на преобразование однородных координат:

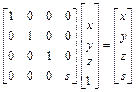 ,                          (1.26)

где s > 0.

Физические декартовы координаты вектора будут равны:

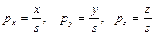 .                     (1.27)

Таким образом, четвертый диагональный элемент однородной матрицы преобразования определяет глобальное сжатие координат, если s>1, и растяжение, если 0<s<1. В задачах кинематики МР параметр s принимается равным 1.

Таким образом, однородная матрица преобразования переводит вектор, заданный однородными координатами в системе координат OUVW, в абсолютную систему координат ОXYZ: 

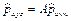.                               (1.28а)

Поскольку мы приняли глобальный масштабирующий множитель s равным единице, то в дальнейшем будем опускать знак «^» в обозначении векторов, представленных в однородных координатах.

Матрица однородных преобразований может быть записана и в общем виде, который мы будем использовать ниже, при ее обращении:

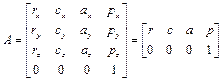                (1.28б)

1.4.2. Геометрический смысл матрицы однородных преобразований

24

В общем случае матрица однородных преобразований векторов трехмерного пространства может быть представлена так, как в равенстве (1.28б). Выберем в системе координат OUVW точку P, имеющую однородные координаты (0, 0, 0, 1)^Т, т. е. вектор р_uvw совпадает с началом системы координат OUVW. В этом случае верхняя правая подматрица размерностью 3х1 характеризует положение точки начала системы координат OUVW в абсолютной системе координат OXYZ. Далее, выберем точку P равной (1, 0, 0, 1)^T, т. е. р_uvw тождественно равно i_u. Кроме того, предположим, что начала обеих систем отсчета совпадают и расположены в точке О. Это приводит к тому, что все элементы верхней правой подматрицы, имеющей размерность 3х1, равны 0. Тогда первый столбец (вектор r) однородной матрицы преобразования определяет координаты единичного вектора оси ОU системы OUVW в системе координат OXYZ. Аналогично, полагая P равным (0,1,0,I)^T и (0,0,1,1)^T, легко видеть, что второй столбец (вектор c) и третий столбец (вектор а) элементов однородной матрицы преобразования определяют ответственно координаты единичных векторов осей OV и OW системы OUVW в абсолютной системе координат. Таким образом, если задана абсолютная система координат OXYZ и однородная матрица преобразования A, то векторы-столбцы подматрицы поворота представляют собой единичные векторы в направлении осей системы OUVW, заданные своими координатами в абсолютной системе координат, т. е. задают ориентацию основных осей системы координат OUVW относительно абсолютной системы координат. Четвертый вектор-столбец матрицы однородных преобразований задает положение начала координат системы OUVW относительно абсолютной системы координат. Другими словами матрица однородных преобразований в геометрическом смысле определяет расположение связанной (подвижной) системы координат (положение и ориентацию) по отношению к абсолютной (неподвижной) системе координат [3].

Поскольку операция обращения подматрицы поворота R _{3 x 3} совпадает, в соответствии с выражением (1.11), с операцией транспонирования, то векторы-строки подматрицы поворота задают положения основных осей абсолютной системы координат относительно связанной системы координат OUVW. Однако для матрицы однородных преобразований операции обращения и транспонирования не совпадают. Положение начала абсолютной системы координат относительно системы координат OUVW можно определить лишь после того, как определена матрица, обратная матрице однородного преобразования. В общем случае такая матрица имеет следующий вид:

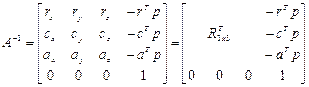. (1.29)

 

Таким образом, из выражения (1.29) видно, что векторы-столбцы матрицы, обратной к однородной матрице преобразования, определяют положение основных осей абсолютной системы координат относительно связанной системы координат OUVW. Верхняя правая подматрица размерностью 3х1 характеризует положение начала абсолютной системы координат относительно системы OUVW.

Пример 1.3. Требуется найти матрицу однородных преобразований, обратную матрице A, где .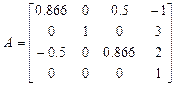

Решение.

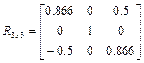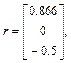
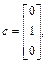
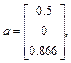
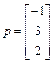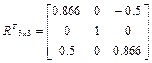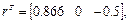
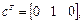
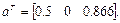В соответствии с принятыми в выражении (1.28б) обозначениями , . Следовательно,  и  В соответствии с выражением (1.29) имеем:

.

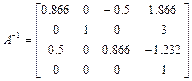Отметим еще раз, что для обращения матриц однородных преобразований не требуется использования стандартных процедур, а достаточно лишь знать их свойства, отраженные в выражении (1.29).

Рассмотрим еще один пример, требующий обращения матрицы однородных преобразований и использования правила «последовательных преобразований» [3] при определении искомой матрицы.

Пример 1.4. Имеется робототехнический комплекс, представленный на рис. 1.8 и состоящий из двух манипуляционных роботов (на рисунке схематично представлены только конечные звенья второго робота).

 

 

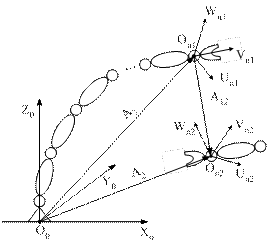
Рис. 1.8. К примеру 1.4

 

Известна матрица однородных преобразований A ₁, описывающая в текущий момент времени положение схвата первого робота в некоторой неподвижной системе координат O ₀ X ₀ Y ₀ Z₀. Также известна матрица A ₂, описывающая положение схвата второго робота, в тот же момент времени и в той же неподвижной системе координат. Для согласования работы роботов требуется определить матрицу A ₁₂ , описывающую положение схвата второго робота, в системе координат     O_{n 1} U_{n 1} V _{n 1} W _{n 1}, жестко связанной со схватом первого робота, если:

, .

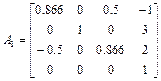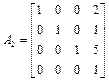Решение.

В соответствии с правилом «последовательных преобразований» [3] и поставленной задачей, матрицы однородных преобразований, в соответствии с рис. 1.8, должны удовлетворять равенству:

A ₁ A ₁₂ = A ₂ .                              (1.30)

Следует обратить внимание на направление преобразований, задаваемых на рис.1.8 стрелками. Так, например, если бы требовалось определить положение схвата первого робота в системе координат O_n2U_n2V_n2W_n2, жестко связанной со схватом второго робота, то преобразование A ₁₂ имело бы противоположное направление и было бы справедливо следующее равенство:

 

A ₂ A ₁₂ = A ₁ .

 

В любом случае, при решении задач такого рода, необходимо составлять равенства, отражающие последовательность преобразований по замкнутому контуру.

В соответствии с выражением (1.30) имеем:

A ₁₂ = A ₁ ^-1 A ₂ .

Матрица A ₁ ^-1 определена нами в примере 1.3. В соответствии с последним равенством имеем:

.

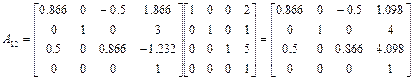Найденная матрица A ₁₂  является решением поставленной задачи.

 

1.4.3. Матрица композиции однородных преобразований

Матрица композиции однородных преобразований может быть получена путем перемножения однородных матриц элементарных поворотов и сдвигов. Однако поскольку операция перемножения матриц некоммутативная, особое внимание следует обратить на порядок перемножения этих матриц. При определении матрицы композиции однородных преобразований будут полезны следующие правила [3], аналогичные тем, которые были рассмотрены в п. 1.3 для матриц элементарных поворотов:

1. Вначале обе системы координат совпадают, и, следовательно, матрица однородных преобразования представляет собой единичную матрицу I₄ размерностью 4х4.

2. Если подвижная система координат OUVW совершает поворот/сдвиг относительно осей неподвижной системы OXYZ, матрицу предыдущего результирующего однородного преобразования надо умножить слева на соответствующую однородную матрицу поворота/сдвига.

3. Если подвижная система координат OUVW совершает поворот/сдвиг относительно одной из собственных осей, матрицу предыдущего результирующего однородного преобразования надо умножить справа на соответствующую однородную матрицу элементарного поворота /сдвига.

Пример 1.5. Требуется определить матрицу 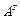, задающую преобразование, состоящее из поворота на угол  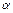вокруг оси OX, затем смещения на b единиц вдоль оси OV подвижной системы координат [3].

Решение. Следуя изложенным выше правилам, и, учитывая тот факт, что матрица 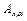 преобразует ось О Y в ось OV, а осям О Y и OV соответствует одна и та же матрица сдвига (1.24), имеем:

 

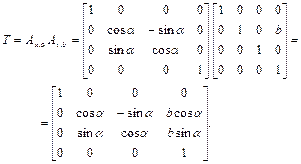
В настоящем параграфе определены две системы координат - неподвижная абсолютная система координат OX Y Z и подвижная система, совершающая вращательное и поступательное движение, - система координат OUVW. Для описания взаимного пространственного положения этих систем координат была использована матрица однородных преобразований размерностью 4х4. Матрица однородных преобразований обладает тем свойством, что, воздействуя на вектор положения, выраженный в однородных координатах, производит одновременно преобразования поворота, сдвига перспективы и глобальное изменение масштаба [3].

28

Если эти две системы координат связать со звеньями механической системы манипуляционного робота, например с i-м и (i -1)-м звеньями соответственно, то система координат (i-1)-го звена будет абсолютной системой координат, а система координат i-го звена, если последнее движется, - подвижной системой координат. Используя матрицу А, мы по известным координатам р _i, неподвижной относительно i-го звена точки P в системе OUVW i-го звена, можем получить координаты этой точки в системе координат OXYZ, связанной с (i- 1)-м звеном, в соответствии со следующей формулой:

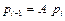,                                                 (1.31)

где A − матрица однородных преобразований, устанавливающая связь между системами координат; р_i − расширенный вектор положения (x _i , y _i ,z _i , l) ^T, определяющий однородные координаты точки в системе координат i-го звена; р _{i -1} − расширенный вектор положения ( x_{i -1} , y_{i -1} , z_{i -1} , l ) ^T, определяющий однородные координаты этой же точки р_i, относительно системы координат (i -1)-го звена.

Возникает вопрос: а как получить матрицу однородных преобразований A, которая бы отражала кинематическую связь между двумя звеньями механической системы манипуляционного робота? Иными словами: если рассматривать два произвольных соседних звена кинематической цепи и с каждым из них жестко связать собственную систему координат, то как друг относительно друга расположены эти системы в процессе изменения обобщенной координаты q_i в сочленении? Ответы на эти вопросы были получены Денавитом и Хартенбергом в их известной работе [4]. Им удалось найти общий вид матрицы A для произвольной кинематической пары пятого класса. Ход их рассуждений и полученные результаты представлены в следующем параграфе.

1.5. Преобразование Денавита - Хартенберга

Выбор координат. Последовательность преобразований.               Преобразования Денавита-Хартенберга

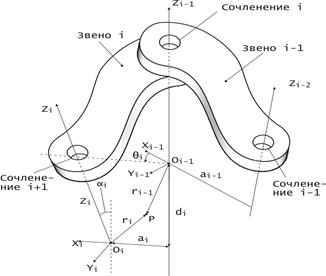
Предположим, что задана кинематическая пара пятого класса, представленная на рис. 1.9 и состоящая из двух звеньев, (i -1)-го и i-го, механической системы манипулятора, объединенных i-м сочленением.

Требуется получить матрицу однородных преобразований A общего вида (1.28б), описывающую взаимное расположение систем координат, жестко связанных со звеньями кинематической пары. Причем с i-м звеном связана система O_iX_iY_iZ_i, а с (i-1)-м – система O_i-1X_i-1Y_i-1Z_i-1.

Системы координат строятся следующим образом:

1. Ось координат O_iZ_i направлена вдоль оси (i +1 )–го сочленения (оси перемещения или вращения (i +1 )–го звена).

2. Проведем перпендикуляр между осями O_iZ_i и O_{i -1} Z_{i -1} таким образом, чтобы длина перпендикуляра а _i являлась минимальным расстоянием между осями O_iZ_i и O_{i -1} Z_{i -1}. Если оно равно нулю, то направление вектора а _i становится произвольным. Заметим, что а_i имеет смысл длины i-го звена.

3. Ось O_iX_i перпендикулярна осям O_iZ_i и O_{i -1} Z_{i -1} и направлена от оси O_{i -1} Z_{i -1} (так, чтобы образовать правостороннюю систему координат либо с O_iZ_i и O_{i -1} Z_{i -1}, либо с O_{i -1} Z_{i -1} и O_iZ_i ).

4. Ось координат O_iY_i выбирается так, чтобы система координат O_iX_iY_iZ_i была правосторонней.

5. Расстояние между двумя общими перпендикулярами a_i и a _{i -1} называется звенным расстоянием d _i .

6. Угол ориентации оси O_iX_i относительно оси O_{i -1} X _i-l обозначим 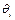и назовем компонентой вектора углов в сочленениях.

7. Угол ориентации оси O_iZ_i относительно оси O_{i -1} Z_{i -1} обозначим 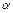_i и назовем компонентой вектора углов скручивания.

 

Рис. 1.9. Системы координат и параметры кинематической пары пятого класса

 

30

30

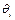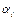Четыре параметра d _i , , , а_i составляют минимальный набор, необходимый для описания кинематической конфигурации каждой кинематической пары механической системы робота. Заметим, что d_i − звенное расстояние, 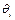− угол в сочленении, a_i − длина звена, 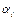− угол скручивания звена. Для плоскостного поворотного сочленения в общем случае d _i , a_i и  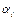являются константами, а  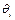изменяется при повороте звена i относительно оси i-го сочленения. С другой стороны, для призматического сочленения 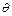_i, a_i и  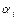− константы, а d_i изменяется при поступательном движении звена i вдоль оси i-го сочленения. Таким образом, в обоих случаях а _i и 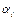обычно неизменны и зависят от конструкции робота. Например, если оси соседних сочленений пересекаются, то длина звена а _i равна 0 (как в случае с призматическим сочленением) [4].

Если система координат Денавита-Хартенберга для каждого звена описана, то можно легко получить матрицу однородных преобразований в i-й системе координат относительно (i-1)-ой системы. Положим, что i-я система координат является подвижной относительно (i-1)-ой системы координат (аналог системы OUVW, рассмотренной в предыдущем параграфе). В соответствии с рис. 1.9 точка Р, описанная в i-ой системе координат через вектор r_i, может быть описана в ( i-1)-й системе координат через вектор r_i-1 посредством последовательного выполнения следующих преобразований [4]:

1. Поворот относительно оси O_{i -1} Z_{i -1} на угол 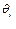, чтобы оси O_iX_i , O_{i -1} X _i-l стали параллельны: A_{Zi -1, .}

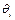2. Перенос вдоль оси O_{i -1} Z_i-1 на расстояние d _i, чтобы совместить оси O_iX_i, O_{i -1} X _i-l : A_{zi -1, d} .

3. Перенос вдоль оси O_iX_i на расстояние а_i для совмещения двух начал систем координат: A_{xi , ai}.

4. Поворот относительно оси O_iX_i на угол 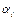, для полного совпадения двух систем координат: .

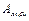Таким образом, полное преобразование, связывающее i-е звено с (i-1)-м, в соответствии с правилами, представленными в п.1.4.3., имеет вид

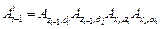                                   (1.32)

или

 

 

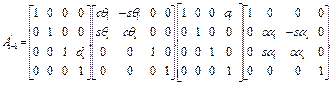
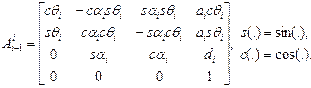     (1.33)

 

Матрица (1.33), отражающая связь между системами координат O_iX_iY_iZ_i и O_{i -1} X_{i -1} Y_{i -1} Z_{i -1} , жестко связанными с i-м и (i -1)-м звеньями соответственно, и является матрицей преобразования Денавита-Хартенберга. В последующем параграфе мы используем ее для решения прямой задачи кинематики (1.1).