Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Матрицу поворота размерностью 3х3 можно определить как матрицу преобразования трехмерного вектора положения в евклидовом пространстве, переводящую его координаты из подвижной (связанной) системы координат OUVW в неподвижную (абсолютную) систему координат OXYZ. Приведем процедуру получения матриц элементарных и сложных поворотов, представленную в [3]. На рис. 1.5 показаны две правые прямоугольные системы координат: система координат OXYZ с осями OX, О Y , OZ и система OUVW с осями О U , OV, OW. Начала этих систем совпадают и расположены в точке О.

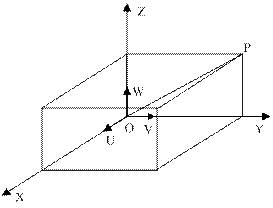
Рис. 1.5. Абсолютная и связанная системы координат

 

14

Система OXYZ фиксирована в трехмерном пространстве и принята за абсолютную, а система координат OUVW вращается относительно осей абсолютной системы OXYZ и собственных осей. Физически система OUVW может рассматриваться как связанная система координат. Это означает, что она соответствующим образом жестко связана с твердым телом (например, с летательным аппаратом или звеном манипулятора) и движется вместе с ним [3]. 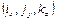Пусть  и 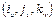 -единичные векторы, направленные вдоль осей систем ОХ YZ и OUVW соответственно.

Некоторую точку P в пространстве можно охарактеризовать координатами относительно любой из указанных систем. Предположим, что точка P фиксирована и неподвижна в системе координат OUVW. Тогда в системах координат OUVW и OXYZ точка P будет иметь соответственно координаты

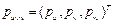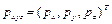, ,                (1.3)

где векторы 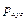 и 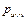 характеризуют положение одной и той же точки P относительно различных систем координат.

Наша задача состоит в том, чтобы определить матрицу R размерностью 3х3, которая преобразует координаты вектора 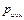 в координаты вектора  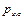в системе OXYZ после того, как система OUVW будет повернута, т. е.

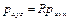.                                           (1.4)

Заметим еще раз , что физически точка P вращается вместе с системой координат OUVW. Из определения компонент вектора имеем

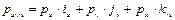,                              (1.5)

где 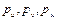 представляют собой составляющие вектора P вдоль осей ОU, OV и OW соответственно, или проекции вектора P на эти оси. Таким образом, используя определение скалярного произведения и равенство (1.5), получаем

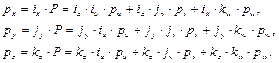            (1.6)

Или, в матричной форме:

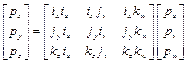.                          (1.7)

С учетом выражения (1.7) матрица R в равенстве (1.4) принимает вид

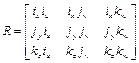.                             (1.8)

Аналогично, координаты 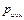 можно получить из координат :

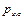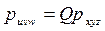.                                     (1.9)

Или

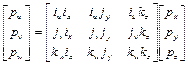 .                    (1.10) 

Поскольку операция скалярного произведения коммутативна, то из соотношений (1.8)-(1.10) следует:

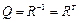 ,                                           (1.11)

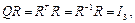                              (1.12)

где 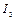 − единичная матрица размерностью 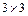. Преобразование, определяемое формулой (1.4) или (1.9), называется ортогональным преобразованием, а поскольку все векторы, входящие в скалярные произведения, единичные, его также называют ортонормированным преобразованием [3].

Особый интерес представляют матрицы поворота системы OUVW относительно каждой из трех основных осей системы OXYZ. Если положение системы OUVW в пространстве изменяется за счет поворота этой системы на угол поворота вокруг оси OX, то в системе отсчета OXYZ изменятся и координаты (p_x, p_y, p_z)^T вектора p_uvw, имеющей в системе O U VW неизменные координаты (p_u, p_v, p_w ). Соответствующая матрица преобразования R_x,α называется матрицей поворота вокруг оси OX на угол α.. Основываясь на полученных выше результатах, для матрицы R_x,α имеем

 p_xyz = R_x,α p_uvw,                                                                      (1.13)

причем i_x 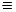i_u, и

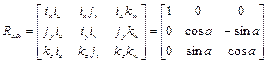.               (1.14)

Аналогично, ( 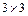) матрицы поворота вокруг оси ОУ на угол φ и вокруг оси OZ на угол θ имеют соответственно вид (рис. 1.6)

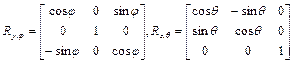 .     (1.15)

Причем как в рассматриваемых случаях, так и в дальнейшем за положительное направление поворота мы будем принимать движение соответствующей системы координат против часовой стрелки.

Матрицы R_x,α, R_y,φ, R_z,θ называются матрицами элементарных поворотов. Любые другие матрицы конечных поворотов можно получить, используя матрицы элементарных поворотов.

Пример 1.1. В подвижной, связанной системе координат OUVW заданы две точк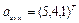и  и 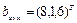. Требуется определить координаты a_xyz и b_xyz этих точек в абсолютной системе координат, если система OUVW повернута относительно оси O Y на угол 30°.

Решение: 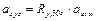 и ,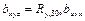

,

.

 

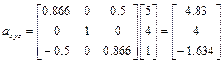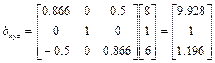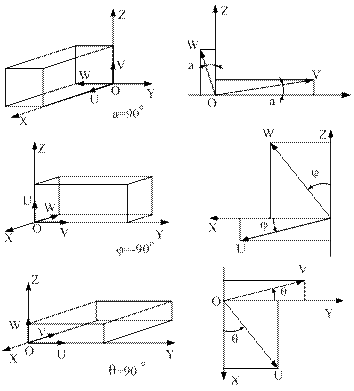
Рис. 1.6. Поворот связанной системы координат относительно осей абсолютной системы координат

 

17

1.3.2. Матрицы сложных поворотов

Описание последовательности конечных поворотов относительно осей системы OXYZ можно получить путем перемножения матриц элементарных поворотов. Поскольку операция перемножения матриц некоммутативна, здесь существенна последовательность выполнения поворотов и, следовательно, последовательность перемножения соответствующих матриц. Например, матрица поворота, представляющего собой результат последовательного выполнения поворотов сначала на угол θ вокруг оси OZ, затем на угол α вокруг оси OX, затем на угол φ вокруг оси OY, имеет вид

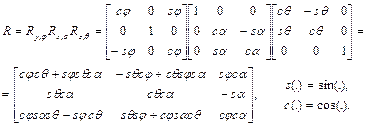 (1.16)

 Она отличается от матрицы, описывающей результат поворота сначала на угол φ вокруг оси OY, затем на угол θ вокруг оси OZ и, наконец, на угол α относительно оси OX. Во втором случае результирующая матрица поворота имеет вид

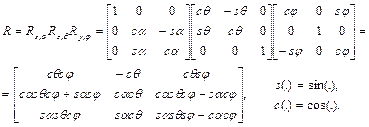(1.17)

Наряду с вращением относительно осей абсолютной системы координат OXYZ подвижная система координат OUVW может совершать повороты вокруг собственных осей. В этом случае результирующая матрица поворота может быть получена с использованием следующих простых правил:

1. Вначале предполагаем, что обе системы координат совпадают, и, следовательно, матрица поворота представляет собой единичную матрицу размерностью .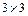

2. Если подвижная система координат OUVW совершает поворот вокруг одной из осей системы OXYZ, то матрицу предыдущего результирующего поворота надо умножить слева на соответствующую матрицу элементарного поворота.

3. Если подвижная система координат OUVW совершает поворот вокруг одной из своих осей, то матрицу предыдущего результирующего поворота надо умножить справа на соответствующую матрицу элементарного поворота.

Пример 1.2. Требуется найти матрицу поворота подвижной системы OUVW, являющуюся результатом последовательности выполнения поворотов сначала на угол α вокруг оси OU, затем на угол φ вокруг оси OY и на угол θ вокруг оси OW.

 Решение:

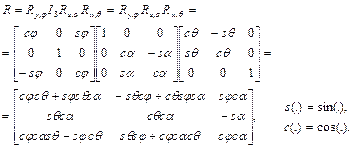
Этот пример построен так, что матрица результирующего поворота такая же, как в выражении (1.16), однако последовательность поворотов отличается от последовательности, результатом которой является выражение (1.16).