В предыдущем параграфе мы рассматривали механическую систему манипуляционного робота (манипулятор) как разомкнутую цепь, которая состоит из нескольких твердых тел (звеньев), последовательно соединенных вращательными или поступательными сочленениями, приводимыми в движение силовыми приводами, размещенными, как правило, в этих сочленениях. То есть, изменяя, посредством i-го привода значение обобщенной координаты q_i (или всех координат одновременно), мы тем самым изменяем положение рабочего органа МР в пространстве внешних координат 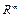, т.е. координаты 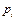. Как правило, в каждом из сочленений размещается датчик соответствующей координаты .

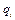Тогда возникает вопрос: как, зная значения обобщенных координат q_i или положение МР в пространстве обобщенных координат 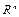, определить положение рабочего органа МР в пространстве внешних координат ?

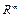То есть, для конкретного МР по известному вектору обобщенных координат 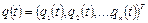 (n - число звеньев) и заданным геометрическим параметрам звеньев требуется определить положение и ориентацию рабочего органа манипулятора относительно системы внешних координат. Иными словами, требуется получить зависимость вектора внешних координат  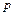в функции элементов вектора  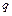вида:

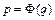,                                               (1.1)

где Ф: 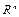→ 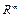- оператор перехода из пространства  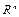в пространство .

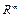Получение функциональной зависимости вида (1.1) и составляет суть решения прямой задачи кинематики.

С другой стороны, при организации перемещений МР движение его рабочего органа планируют в пространстве внешних координат R^m, задавая желаемое положение схвата (лазера, сварочного аппарата и т.п.) или желаемую траекторию его движения в функции координат p_i. Естественно возникает вопрос: а как изменить посредством силовых приводов значения координат q_i, чтобы МР осуществил заданную программу движения? То есть, при известных геометрических параметрах звеньев требуется найти все возможные векторы обобщенных координат МР, обеспечивающие заданные положение и ориентацию схвата относительно системы внешних координат. Иными словами, требуется получить зависимость уже вектора обобщенных координат 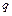 в функции элементов вектора внешних координат  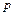вида:

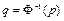,                                                   (1.2)

где Ф^-1: R^m → Rⁿ - оператор перехода из пространства 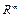 в пространство .

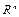Нахождение зависимостей вида (1.2) составляет суть решения обратной задачи кинематики.

Взаимосвязь между прямой и обратной задачами кинематики поясняется на рис. 1.4.

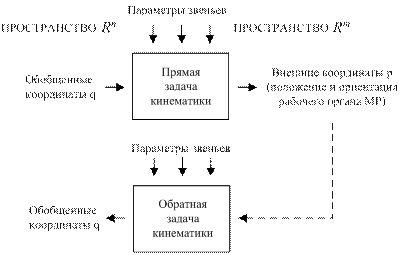
Рис. 1.4. Взаимосвязь прямой и обратной задач кинематики

Так как звенья манипулятора совершают вращательное или поступательное движение относительно системы внешних координат, результирующее пространственное положение рабочего органа МР определяется угловым и поступательным движениями звеньев. В работе [3] изложен общий систематический подход к описанию пространственного расположения звеньев манипулятора в неподвижной системе внешних координат, основанный на применении матричной алгебры. Для описания взаимного пространственного положения двух смежных звеньев этот подход использует однородную матрицу преобразования размерностью 4х4. Прямая задача кинематики сводится тем самым к определению однородной матрицы преобразования, характеризующей пространственное положение системы координат рабочего органа МР в системе внешних координат. Матрицы однородных преобразований используются также при выводе уравнений динамики движения манипулятора.

К решению обратной задачи кинематики существует, вообще-то говоря, несколько подходов [3]. Наиболее часто используются геометрический подход, методы матричной алгебры и численные методы. На примере решения обратной задачи кинематики для простейших механических систем мы рассмотрим геометрический подход и метод Ньютона.

Ниже, в последующих параграфах, изложены основные понятия матричной и векторной алгебры, применяемые для систематического и обобщенного подхода к описанию и представлению расположения звеньев манипулятора относительно заданной неподвижной системы внешних координат. Для описания вращательного движения связанной системы координат относительно неподвижной используется матрица поворота размерностью 3х3, для представления векторов положения в трехмерном пространстве применяются однородные координаты, а для учета поступательного движения связанной системы координат вместо матрицы поворота используются матрицы однородных преобразований размерностью 4х4. Таким матричным представлением для описания пространственной геометрии манипулятора впервые воспользовались Денавит и Хартенберг [4]. Их представление дает универсальный алгоритм для решения задач кинематики и будет рассмотрено ниже.