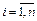Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

10

Независимые координаты взаимного расположения звеньев, однозначно описывающие состояние кинематической цепи МР, называются обобщенными координатами и обычно обозначаются как q_i, , здесь n– число звеньев МР. Независимые координаты, описывающие положение и ориентацию рабочего органа МР в некоторой неподвижной, базовой системе координат, будем называть внешними (базовыми, рабочими или абсолютными) и обозначать как p_j, 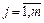, здесь m-число координат. Поскольку положение свободного твердого тела в пространстве описывается шестью координатами (три координаты описывают положение центра системы координат, жестко связанной с твердым телом, а три другие координаты - ориентацию осей связанной системы координат относительно осей базовой системы координат), то .

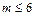Соответственно, производные по времени 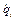,  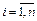от обобщенных координат будем называть обобщенными скоростями, а производные по времени  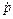от внешних координат - внешними скоростями.

Обобщенные координаты 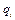 являются элементами пространства обобщенных координат  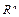размерности 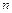, а внешние координаты  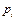– пространства внешних координат размерности 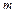, которое в дальнейшем мы будем обозначать через 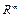. Соответственно и вектор обобщенных координат  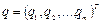имеет размерность n , а вектор внешних координат  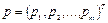- размерность 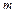, т.е. 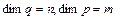. Аналогичные размерности имеют пространства и вектора обобщенных и внешних скоростей.

Число независимых величин, определяющих положение системы в пространстве, принято называть числом степеней свободы этой системы (Degree of Freedom). При принятых предположениях о классе кинематических пар число степеней свободы МР совпадает с количеством звеньев его механической системы и равно n.

Для реализации той или иной технологической задачи требуется m координат. Если, например, требуется организовать перемещение рабочего органа на плоскости, то m =2, если в пространстве - m =3, при предъявлении дополнительных требований к одному из углов ориентации - m =4 и т.д. Количество же звеньев манипулятора может быть различным. Если 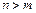, то говорят, что механическая система робота кинематически избыточна. В дальнейшем будем предполагать, что m = n и, соответственно, цепь является кинематически безызбыточной. Так, например, МР с цилиндрической системой координат, представленный на рис. 1.1 и 1.3, имеет три звена и три независимые координаты 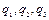, т.е. n =3. При решении технологических задач перемещения схвата на плоскости (m =2) этот робот будет кинематически избыточным и безызбыточным при организации перемещения схвата в пространстве (m =3).