Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В.Х. ПШИХОПОВ

 

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАНИПУЛЯЦИОННЫХ РОБОТОВ

 

Учебник

 

 

Учебник представлен в Федеральный институт развития образования, г. Москва, на предмет получения рецензии в соответствии с требованиями Минобрнауки РФ. Копия договора между ТТИ ЮФУ и ФИРО прилагается.

 

Таганрог 2008

УДК 621. 865

 

В.Х.Пшихопов. Математические модели манипуляционных роботов: Учебник. Таганрог: Изд-во ТТИ ЮФУ, 2008. ____ с.

 

 

Изложены формализованные процедуры вывода математических моделей манипуляционных роботов. Рассмотрены алгоритмы решения задач кинематики разомкнутых кинематических цепей, а также вывода уравнений динамики манипуляторов. Представлены модели динамики манипуляционных роботов в различных пространствах, с учетом двигателей и возможного взаимодействия с внешней средой. Приведены примеры вывода матмоделей. Пособие предназначено для студентов и аспирантов высших учебных заведений.

 

 

Рецензенты:

 

Учебник представлен в Федеральный институт развития образования, г. Москва, на предмет получения рецензии в соответствии с требованиями Минобрнауки РФ. Копия договора между ТТИ ЮФУ и ФИРО прилагается.

 

 

ISBN

 

                                               

 

 

 Ó Пшихопов В.Х., 2008  

 

Содержание

1. Кинематика манипуляционных роботов

1.1. Общие понятия и определения.

1.2. Пространства манипуляционных роботов. Постановка

кинематических задач.

1.2.1. Обобщенные и внешние координаты и их пространства.

1.2.2. Прямая и обратная задачи кинематики.

1.3. Матрицы элементарных и сложных поворотов.

1.3.1. Матрицы элементарных поворотов.

1.3.2. Матрицы сложных поворотов.

1.3.3. Матрица поворота вокруг произвольной оси.

1.3.4. Геометрический смысл матриц поворота.

1.4. Матрицы однородных преобразований.

1.4.1. Однородные координаты и матрицы однородных преобразований.

1.4.2. Геометрический смысл матрицы однородных преобразований.

1.4.3. Матрица композиции однородных преобразований.

1.5. Преобразование Денавита – Хартенберга.

1.6. Решение прямой задачи кинематики (ПЗК).

1.6.1. Построение связанных систем координат.

1.6.2. Определение параметров звеньев.

1.6.3. Определение матрицы манипулятора .

1.6.4.Решение ПЗК.

1.7. Решение ПЗК на примере манипуляционного трехзвенника.

1.8. Применение решений ПЗК в задачах робототехники.

1.8.1. Определение базовых координат по показаниям датчиков обобщенных координат.

1.8.2. Понятие матрицы Якоби для решения ПЗК и вырожденные конфигурации робота.

1.9. Методы и подходы к решению обратной задачи кинематики (ОЗК).

1.9.1. Аналитический подход к решению ОЗК.

1.9.2. Геометрический подход к решению ОЗК.

1.9.3. Численные методы решения ОЗК.

2. Динамика манипуляционных роботов

2.1. Уравнения Лагранжа-Эйлера для голономных систем. Динамика материальной точки.

2.2. Скорость произвольной точки -го звена манипулятора.

2.3. Кинетическая энергия механической системы манипулятора.

2.4. Потенциальная энергия механической системы манипулятора.

2.5. Математическая модель механической системы робота.

2.6. Динамическая модель манипуляционного двухзвенника.

2.7. Определение динамических коэффициентов для манипуляционных трехзвенников.

2.8. Анализ динамических моделей манипуляционных систем.

2.9. Подходы к упрощению динамических моделей манипуляторов.

2.10. Особенности моделей динамики манипуляторов при решении задач управления.

2.10.1. Динамика манипуляционных роботов с учетом двигателей.

2.10.2. Динамика манипуляторов при силовом взаимодействии с внешней средой.

2.10.3. Уравнения динамики в форме Коши.

2.10.4. Динамика манипулятора в пространстве внешних координат.

        2.10.5. Динамика манипуляторов на многообразиях.
Введение

 

По оценкам экспертов ООН в самое ближайшее время нашу цивилизацию ожидает бум в развитии робототехники сродни тому, который имел место в 80-х – 90-х годах прошлого века в области компьютеров и компьютерных технологий. Уже начиная с 2002 года, японская фирма Honda приступила к серийному выпуску антропоморфных (человекоподобных) роботов, предназначенных для использования в социальных программах японского правительства. Бурными темпами развивается микроробототехника (хирургические роботы, микророботы военного назначения и т.д.) и робототехника экстремальных сред (космические и подводные роботы, планетоходы и т.д.). От соревновательных программ в сторону реального производства движется развитие мобильных роботов. Укрепляют свои позиции манипуляционные роботы как основной элемент гибких производственных систем. Другими словами, робототехника вторгается в новые области человеческой деятельности, заменяя человека в рутинных операциях, вредных и агрессивных средах, в военной сфере, в исследовании космического пространства и т.п.

 Очевиден междисциплинарный характер робототехники как интегральной науки. Сегодня ее содержание определяют теория систем и теория управления, теория проектирования проблемно-ориентированных вычислительных систем, теория и аппаратно-программные средства параллельных и распределенных вычислений, систем сбора и обработки информации и т.д.

Какова роль специалистов в области теории управления в бурном процессе развития этой относительно новой отрасли человеческой деятельности? Ответ очевиден: даже при самой современной программно-аппаратной базе невозможно создать эффективное робототехническое устройство, не зная и не используя научных методов и подходов, высокоэффективных структурно-алгоритмических решений, которые предоставляет сегодня современная теория управления.

С другой стороны, подход к задачам управления, и не только роботами, требует наличия определенных этапов в процессе их решения. И первый из них – это вывод корректных математических моделей, с различной степенью адекватности отражающих тот или иной реальный объект или процесс.

В настоящем учебнике на основе формализованных процедур, излагаются подходы к выводу математических моделей манипуляционных роботов.

Какова кинематическая связь или как влияют изменения углов поворота и/или перемещения звеньев манипуляционного робота на координаты положения схвата, лазера или другого рабочего органа робота? И, наоборот: по какой программе нужно осуществлять движение звеньев манипулятора, чтобы его рабочий орган описал заданную траекторию движения? Решение этих вопросов, а также необходимый математический аппарат, изложены в первой главе.

Вторая глава посвящена динамике манипуляционных роботов, т.е. математическому описанию взаимосвязи параметров движения роботов (координаты, скорости, ускорения его звеньев) и сил, и моментов, возникающих при этом в сочленениях манипуляторов, функционирующих в различных пространствах.

Без ответов на эти вопросы, без построения адекватной математической модели роботов реализация систем управления ими не приведет к ожидаемым результатам, желаемому качеству и приемлемой точности отработки спланированных траекторий.

При написании учебника использованы как результаты известного формализма, так и оригинальные разработки автора, поясняемые многочисленными примерами.

Настоящий учебник будет полезен не только будущим специалистам в области теории и систем управления, но и всем, кто занимается вопросами проектирования и разработки средств робототехники или сложных механических систем.

Автор хотел бы выразить искреннюю признательность проф. Подураеву Ю.В. (МГТУ «Станкин», г. Москва), проф. Юревичу Е.И., проф. Бурдакову С.Ф. (СПбГТУ, г. С.-Петербург), проф. Манько С.В. и проф. Лохину В.М. (МИРЭА, г. Москва) за благожелательные замечания, послужившие улучшению содержания учебника.

Кинематики

Решение.

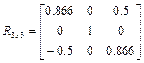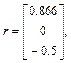
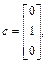
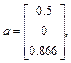
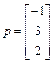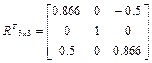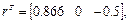
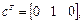
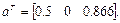В соответствии с принятыми в выражении (1.28б) обозначениями , . Следовательно,  и  В соответствии с выражением (1.29) имеем:

.

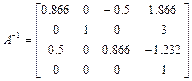Отметим еще раз, что для обращения матриц однородных преобразований не требуется использования стандартных процедур, а достаточно лишь знать их свойства, отраженные в выражении (1.29).

Рассмотрим еще один пример, требующий обращения матрицы однородных преобразований и использования правила «последовательных преобразований» [3] при определении искомой матрицы.

Пример 1.4. Имеется робототехнический комплекс, представленный на рис. 1.8 и состоящий из двух манипуляционных роботов (на рисунке схематично представлены только конечные звенья второго робота).

 

 

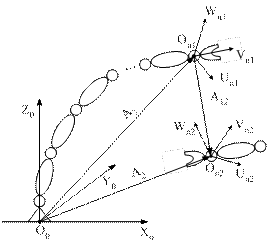
Рис. 1.8. К примеру 1.4

 

Известна матрица однородных преобразований A ₁, описывающая в текущий момент времени положение схвата первого робота в некоторой неподвижной системе координат O ₀ X ₀ Y ₀ Z₀. Также известна матрица A ₂, описывающая положение схвата второго робота, в тот же момент времени и в той же неподвижной системе координат. Для согласования работы роботов требуется определить матрицу A ₁₂ , описывающую положение схвата второго робота, в системе координат     O_{n 1} U_{n 1} V _{n 1} W _{n 1}, жестко связанной со схватом первого робота, если:

, .

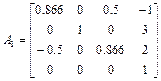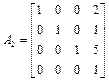Решение.

В соответствии с правилом «последовательных преобразований» [3] и поставленной задачей, матрицы однородных преобразований, в соответствии с рис. 1.8, должны удовлетворять равенству:

A ₁ A ₁₂ = A ₂ .                              (1.30)

Следует обратить внимание на направление преобразований, задаваемых на рис.1.8 стрелками. Так, например, если бы требовалось определить положение схвата первого робота в системе координат O_n2U_n2V_n2W_n2, жестко связанной со схватом второго робота, то преобразование A ₁₂ имело бы противоположное направление и было бы справедливо следующее равенство:

 

A ₂ A ₁₂ = A ₁ .

 

В любом случае, при решении задач такого рода, необходимо составлять равенства, отражающие последовательность преобразований по замкнутому контуру.

В соответствии с выражением (1.30) имеем:

A ₁₂ = A ₁ ^-1 A ₂ .

Матрица A ₁ ^-1 определена нами в примере 1.3. В соответствии с последним равенством имеем:

.

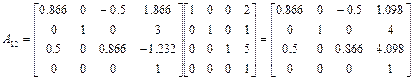Найденная матрица A ₁₂  является решением поставленной задачи.

 

1.4.3. Матрица композиции однородных преобразований

Матрица композиции однородных преобразований может быть получена путем перемножения однородных матриц элементарных поворотов и сдвигов. Однако поскольку операция перемножения матриц некоммутативная, особое внимание следует обратить на порядок перемножения этих матриц. При определении матрицы композиции однородных преобразований будут полезны следующие правила [3], аналогичные тем, которые были рассмотрены в п. 1.3 для матриц элементарных поворотов:

1. Вначале обе системы координат совпадают, и, следовательно, матрица однородных преобразования представляет собой единичную матрицу I₄ размерностью 4х4.

2. Если подвижная система координат OUVW совершает поворот/сдвиг относительно осей неподвижной системы OXYZ, матрицу предыдущего результирующего однородного преобразования надо умножить слева на соответствующую однородную матрицу поворота/сдвига.

3. Если подвижная система координат OUVW совершает поворот/сдвиг относительно одной из собственных осей, матрицу предыдущего результирующего однородного преобразования надо умножить справа на соответствующую однородную матрицу элементарного поворота /сдвига.

Пример 1.5. Требуется определить матрицу 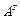, задающую преобразование, состоящее из поворота на угол  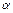вокруг оси OX, затем смещения на b единиц вдоль оси OV подвижной системы координат [3].

Решение. Следуя изложенным выше правилам, и, учитывая тот факт, что матрица 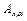 преобразует ось О Y в ось OV, а осям О Y и OV соответствует одна и та же матрица сдвига (1.24), имеем:

 

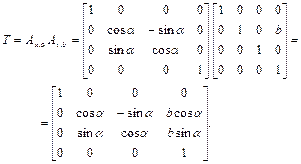
В настоящем параграфе определены две системы координат - неподвижная абсолютная система координат OX Y Z и подвижная система, совершающая вращательное и поступательное движение, - система координат OUVW. Для описания взаимного пространственного положения этих систем координат была использована матрица однородных преобразований размерностью 4х4. Матрица однородных преобразований обладает тем свойством, что, воздействуя на вектор положения, выраженный в однородных координатах, производит одновременно преобразования поворота, сдвига перспективы и глобальное изменение масштаба [3].

28

Если эти две системы координат связать со звеньями механической системы манипуляционного робота, например с i-м и (i -1)-м звеньями соответственно, то система координат (i-1)-го звена будет абсолютной системой координат, а система координат i-го звена, если последнее движется, - подвижной системой координат. Используя матрицу А, мы по известным координатам р _i, неподвижной относительно i-го звена точки P в системе OUVW i-го звена, можем получить координаты этой точки в системе координат OXYZ, связанной с (i- 1)-м звеном, в соответствии со следующей формулой:

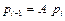,                                                 (1.31)

где A − матрица однородных преобразований, устанавливающая связь между системами координат; р_i − расширенный вектор положения (x _i , y _i ,z _i , l) ^T, определяющий однородные координаты точки в системе координат i-го звена; р _{i -1} − расширенный вектор положения ( x_{i -1} , y_{i -1} , z_{i -1} , l ) ^T, определяющий однородные координаты этой же точки р_i, относительно системы координат (i -1)-го звена.

Возникает вопрос: а как получить матрицу однородных преобразований A, которая бы отражала кинематическую связь между двумя звеньями механической системы манипуляционного робота? Иными словами: если рассматривать два произвольных соседних звена кинематической цепи и с каждым из них жестко связать собственную систему координат, то как друг относительно друга расположены эти системы в процессе изменения обобщенной координаты q_i в сочленении? Ответы на эти вопросы были получены Денавитом и Хартенбергом в их известной работе [4]. Им удалось найти общий вид матрицы A для произвольной кинематической пары пятого класса. Ход их рассуждений и полученные результаты представлены в следующем параграфе.

1.5. Преобразование Денавита - Хартенберга

Выбор координат. Последовательность преобразований.               Преобразования Денавита-Хартенберга

Предположим, что задана кинематическая пара пятого класса, представленная на рис. 1.9 и состоящая из двух звеньев, (i -1)-го и i-го, механической системы манипулятора, объединенных i-м сочленением.

Требуется получить матрицу однородных преобразований A общего вида (1.28б), описывающую взаимное расположение систем координат, жестко связанных со звеньями кинематической пары. Причем с i-м звеном связана система O_iX_iY_iZ_i, а с (i-1)-м – система O_i-1X_i-1Y_i-1Z_i-1.

Системы координат строятся следующим образом:

1. Ось координат O_iZ_i направлена вдоль оси (i +1 )–го сочленения (оси перемещения или вращения (i +1 )–го звена).

2. Проведем перпендикуляр между осями O_iZ_i и O_{i -1} Z_{i -1} таким образом, чтобы длина перпендикуляра а _i являлась минимальным расстоянием между осями O_iZ_i и O_{i -1} Z_{i -1}. Если оно равно нулю, то направление вектора а _i становится произвольным. Заметим, что а_i имеет смысл длины i-го звена.

3. Ось O_iX_i перпендикулярна осям O_iZ_i и O_{i -1} Z_{i -1} и направлена от оси O_{i -1} Z_{i -1} (так, чтобы образовать правостороннюю систему координат либо с O_iZ_i и O_{i -1} Z_{i -1}, либо с O_{i -1} Z_{i -1} и O_iZ_i ).

4. Ось координат O_iY_i выбирается так, чтобы система координат O_iX_iY_iZ_i была правосторонней.

5. Расстояние между двумя общими перпендикулярами a_i и a _{i -1} называется звенным расстоянием d _i .

6. Угол ориентации оси O_iX_i относительно оси O_{i -1} X _i-l обозначим 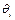и назовем компонентой вектора углов в сочленениях.

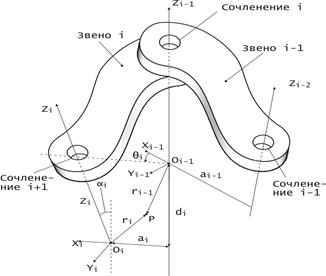
7. Угол ориентации оси O_iZ_i относительно оси O_{i -1} Z_{i -1} обозначим 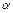_i и назовем компонентой вектора углов скручивания.

 

Рис. 1.9. Системы координат и параметры кинематической пары пятого класса

 

30

30

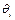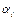Четыре параметра d _i , , , а_i составляют минимальный набор, необходимый для описания кинематической конфигурации каждой кинематической пары механической системы робота. Заметим, что d_i − звенное расстояние, 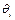− угол в сочленении, a_i − длина звена, 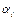− угол скручивания звена. Для плоскостного поворотного сочленения в общем случае d _i , a_i и  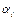являются константами, а  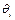изменяется при повороте звена i относительно оси i-го сочленения. С другой стороны, для призматического сочленения 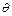_i, a_i и  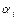− константы, а d_i изменяется при поступательном движении звена i вдоль оси i-го сочленения. Таким образом, в обоих случаях а _i и 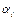обычно неизменны и зависят от конструкции робота. Например, если оси соседних сочленений пересекаются, то длина звена а _i равна 0 (как в случае с призматическим сочленением) [4].

Если система координат Денавита-Хартенберга для каждого звена описана, то можно легко получить матрицу однородных преобразований в i-й системе координат относительно (i-1)-ой системы. Положим, что i-я система координат является подвижной относительно (i-1)-ой системы координат (аналог системы OUVW, рассмотренной в предыдущем параграфе). В соответствии с рис. 1.9 точка Р, описанная в i-ой системе координат через вектор r_i, может быть описана в ( i-1)-й системе координат через вектор r_i-1 посредством последовательного выполнения следующих преобразований [4]:

1. Поворот относительно оси O_{i -1} Z_{i -1} на угол 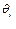, чтобы оси O_iX_i , O_{i -1} X _i-l стали параллельны: A_{Zi -1, .}

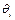2. Перенос вдоль оси O_{i -1} Z_i-1 на расстояние d _i, чтобы совместить оси O_iX_i, O_{i -1} X _i-l : A_{zi -1, d} .

3. Перенос вдоль оси O_iX_i на расстояние а_i для совмещения двух начал систем координат: A_{xi , ai}.

4. Поворот относительно оси O_iX_i на угол 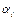, для полного совпадения двух систем координат: .

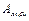Таким образом, полное преобразование, связывающее i-е звено с (i-1)-м, в соответствии с правилами, представленными в п.1.4.3., имеет вид

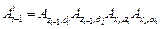                                   (1.32)

или

 

 

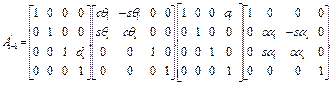
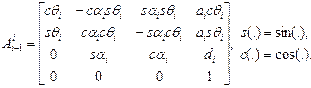     (1.33)

 

Матрица (1.33), отражающая связь между системами координат O_iX_iY_iZ_i и O_{i -1} X_{i -1} Y_{i -1} Z_{i -1} , жестко связанными с i-м и (i -1)-м звеньями соответственно, и является матрицей преобразования Денавита-Хартенберга. В последующем параграфе мы используем ее для решения прямой задачи кинематики (1.1).

 

Таблица 1

Параметры звеньев

Звено, i	di	ai	qi	ai	cosqi	sinqi	cosai	sinai
1
2
…..	…	….	….	….	….	….	….	….
n

 

При определении параметров звеньев следует помнить, что каждая i- я система координат осуществляет движение вместе с i- м звеном.

Если какой − то из параметров невозможно корректно определить по изложенным правилам, то следует еще раз проверить правильность построения систем координат.

Пример 1.7. Для манипуляционного двухзвенника, рассмотренного в примере 1.6 , требуется определить параметры его звеньев.

Решение. Определим координату q₁ как угол между осями O ₀ Y ₀ и O ₁ X ₁ , а q ₂ - как расстояние от точки O ₀ до левого торца второго звена. Тогда, в соответствии с правилами определения параметров, получим их следующие значения, представленные в табл. 2.

Таблица 2

 Параметры звеньев двухзвенника         

Звено	d	a	q	a	cosq	sinq	cosa	sina
1	0	0	p/2+q1	p/2	-sinq1	cosq1	0	1
2	q2+l2	0	0	0	1	0	1	0

 

Решение ПЗК

Теперь отметим наиболее важный момент в разделе кинематики манипуляционных роботов: решение прямой задачи кинематики (1.1) определяется наддиагональными элементами матрицы манипулятора T .

То есть решение ПЗК в общем случае имеет вид

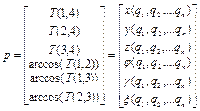,                      (1.37)

где x , y , z - координаты положения характерной точки рабочего органа МР; φ, γ, ξ- углы ориентации системы координат, жестко связанной с рабочим органом МР в базовой, неподвижной системе координат.

Решение ПЗК, представленное векторами (1.1) и (1.37), имеет размерность (mx1). Поскольку мы рассматриваем кинематически безызбыточные манипуляторы, т.е. когда m=n, с кинематическими парами пятого класса, то размерность вектора решения ПЗК определяется количеством звеньев кинематической цепи. Так, для матрицы манипулятора, полученной в примере 1.9, решение прямой задачи кинематики имеет вид

,

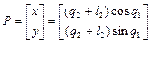где x, y- координаты точки O₂ в базовой системе координат.

Если же пространственный манипулятор имеет три звена, то решением ПЗК являются элементы T(1,4), T(2,4), T(3,4) матрицы манипулятора T.

38

Если же плоский МР имеет три звена, то для кинематически безызбыточной задачи в качестве решения ПЗК мы выбираем два ненулевых элемента вектора p _3х1 (см. обозначения к матрице (1.22)) из матрицы манипулятора и наддиагональный элемент подматрицы R _{3 x 3} матрицы манипулятора, являющийся функцией обобщенных координат.

38

Если же у пространственного манипулятора звеньев больше трех, то мы можем уже определенным образом, если это требуется, ориентировать рабочий орган манипулятора, а не только перемещать его в пространстве базовых координат. В этом случае, в решение ПЗК, помимо всех элементов вектора p _3х1, дополнительно включается соответствующее число независимых, наддиагональных элементов подматрицы R _{3 x 3} матрицы манипулятора, также являющихся функциями обобщенных координат.

Следует отметить еще раз, что размерность вектора 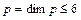. Это означает, что даже при числе звеньев механической системы неплоского манипулятора n>6, т.е. при кинематической избыточности МР размерность вектора p не может быть больше шести.

 

1.7. Решение ПЗК на примере манипуляционного трехзвенника

 

В качестве примера рассмотрим манипуляционный робот (МР) с цилиндрической системой координат и состоящий из трех звеньев. Общий вид МР и направление осей вращения в сочленениях представлены на рис. 1.12, где q ₁ , q ₂ , q ₃ – обобщенные координаты. Такой МР может применяться для выполнения многообразных операций – сборки, монтажа, сортировки, упаковки, погрузки − разгрузки и т. д.

1. Построим связанные системы координат в соответствии с правилами, изложенными в п. 1.6.1 (см. рис. 1.12). Здесь 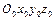- базовая (связанная с неподвижным основанием) система координат;  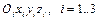- системы координат, жестко связанные с i-ми звеньями.

2.   В соответствии с п. 1.6.2 и рис. 1.12 заполним табл. 3 параметров МР.

Таблица 3

Параметры звеньев трехзвенника             

Звено	d	a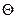
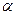
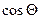
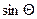
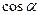
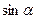
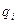
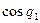
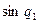
1	0	0		0			1	0
2	q2+0,5l2	-a	0,5π	0,5π	0	1	0	1
3		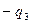0	0	0	1	0	1	0

 

3. Для каждой кинематической пары, используя преобразование Денавита-Хартенберга (1.33), получим матрицы однородных преобразований систем координат:

 

; ;

.

 

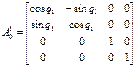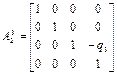4. Примем точку O₄ за характеристическую точку схвата и вычислим матрицу манипулятора как произведение матриц:

 

= ,

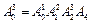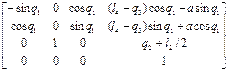где 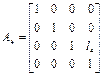, здесь l ₄ - аппликата точки O₄ в системе координат третьего звена.

 

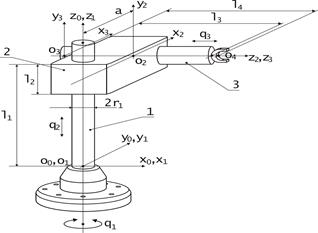
Рис. 1.12. Трехзвенный манипулятор

 

В соответствии с п. 1.6.4 решение ПЗК для представленного манипулятора имеет вид:

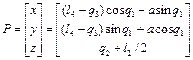.                      (1.38)

Для самопроверки можно подставить фиксированные значения обобщенных координат в решение ПЗК и сравнить значения базовых координат схвата с получаемыми из геометрических соображений по рис. 1.13.

Рис. 1.13. Рабочая зона МР с цилиндрической системой координат

 

Обобщенных координат

Предположим, что в сочленениях механической системы МР помимо двигателей размещены датчики обобщенных координат. Кстати говоря, все роботы, имеющие систему управления, построенную по принципу обратной связи, имеют такие датчики для формирования сигнала, соответствующего состоянию i-й обобщенной координаты. Это необходимо для формирования вектора ошибки, используемого регуляторами системы управления. Т.е. в любой момент времени или с определенной дискретностью, в случае использования цифровых датчиков, мы можем определить взаимное расположение звеньев, описываемое набором обобщенных координат q . Но каково при этом положение рабочего органа манипуляционного робота в пространстве базовых (внешних, рабочих) координат? Ответ на поставленный вопрос является очевидным. Достаточно подставить значения обобщенных координат, снимаемые с соответствующих датчиков, в выражение (1.37) и вычислить по ним значения базовых координат.

Пример 1.10. Определить положение схвата робота, рассмотренного в п. 1.7, при следующих значениях конструктивных параметров: l ₄=0,5 м, l₂=0,1 м, а=0,5 м, если q₁=60^o, q₂=0,6 м, q₃=0,1 м.

Решение. Подставим значения параметров и обобщенных координат в выражение (1.38). Получим:

.    (1.39)

Конечно же, положение схвата или любого другого рабочего органа МР можно определить и с помощью более мощных, внешних сенсорных средств, например телевизионных камер или лазерного дальномера, но это требует дополнительных и аппаратно-алгоритмических, и финансовых затрат.

 

А. Н. Иконниковым)

# Рестарт программы

> restart:

# Подключение библиотеки plots.

> with(plots):

# Подключение библиотеки linalg.

> with(linalg):

# Задание кинематических параметров МР (см. пример 1.11).

> l 4:=0.5; l 2:=0.1 ; a :=0.5 ;

# Ввод решения ПЗК.

>p:=matrix(3,1,[(l4-q3)*cos(q1)-a*sin(q1),(l4-q3)*sin(q1)+a*cos(q1),q2+l2/2]);

# Вызов процедуры workspace, где задаются параметры N1,N2,N3- число расчетных точек по каждой из координат q_i и диапазон изменения каждой координаты (см. пример 1.11).

> tree_zveno:=workspace(p,N1,N2,N3,q1=-0.9*Pi..0.9*Pi, q2=0..1, q3=0..0.3):

# Построение рабочей зоны.

> display(tree_zveno,style=patch,scaling=UNCONSTRAINED);

Значения

Параметра

Шаг итерации

0 1 2 3 1, град 80 54,132 60,923 59,989 q 2, м 0,8 0,600 0,600 0,600 q 3, м 0,13 0,179 0,094 0,100 Δx , мм 195 -16 7 0 Δy , мм 145 43 2 0 Δz , мм -200 0 0 0

 

Из табл. 4 видно, что обобщенные координаты принимают значения q=(59,989, 0,6, 0,1)^Т, удовлетворяющие поставленной задаче, уже на 3-м шаге итерации. Результаты решения ОЗК согласуются с полученными нами в примере 1.10, п. 1.8.1.

Следует отметить, что в области больших отклонений нулевого приближения от истинного значения корней уравнения (1.50), процедура, основанная на выражении (1.51), может и не дать устойчивых решений. Кроме того, найденные в результате итераций значения могут и не принадлежать области допустимых значений аргумента. Так, например, уже при q₁₀=90^o использование метода Ньютона дает значение q₃=0,899, что невозможно в силу конструктивных особенностей рассматриваемого манипулятора, поскольку должно соблюдаться очевидное условие: q₃<l₄=0.5. Поэтому при больших начальных отклонениях аргумента рассматриваемых функций от искомых значений их корней используются градиентные методы [10].

52

Суть градиентных методов заключается в пошаговом приближении к решению уравнения (1.50) в соответствии с выражением

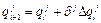,                              (1.52)

где 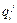- i-е приближение j- й координаты; δ- «направление» i-го шага; Δ 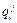- величина i-го шага по j- ой координате.

Причем значения δ и Δ 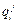 выбираются таким образом, чтобы минимизировать значения функции 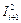. Т.е. требуется выполнение следующей последовательности неравенств:

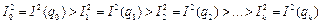 , (1.53)

здесь k- конечный шаг итерации.

В этом случае функция I (1.50) называется функцией невязки. Получаемые промежуточные значения обобщенных координат 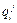могут быть использованы при формировании траектории перехода j-го звена из точки 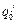в точку 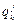, определяемую желаемым положением рабочего органа МР.

Естественно, при использовании численных методов решения ОЗК на каждом шаге итерации, необходимо удовлетворять ограничениям, накладываемым на обобщенные координаты и ориентацию рабочего органа МР, а также учитывать наличие препятствий, расположенных в рабочем пространстве манипулятора.

Для более детальной проработки вопросов, связанных с решением ОЗК, рекомендуется литература [3, 11].

Следует отметить, что в работе [6] предложены подходы к управлению манипуляционными роботами, не требующие решения обратной задачи кинематики.

Решение.

Уравнение динамики двухзвенника имеет вид (2.29) и ,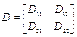

, , .

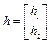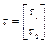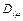73

Определим коэффициенты матрицы инерции , используя выражения (2.31) и (2.32):

,

.

,

.

,

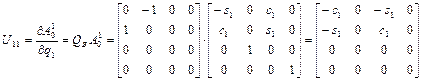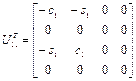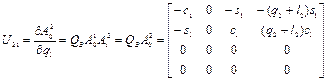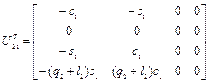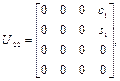
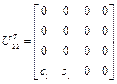здесь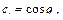

, ,

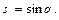
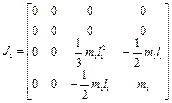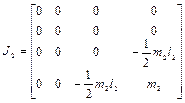где 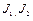- матрицы моментов инерции соответствующих звеньев, полученные по правилам, изложенным в п.2.3,

,

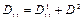где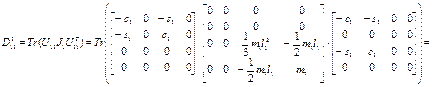

.

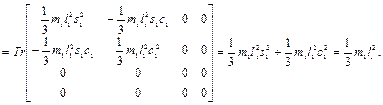
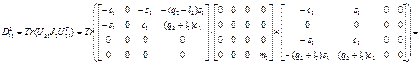
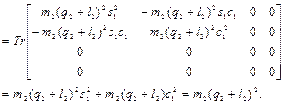Следовательно,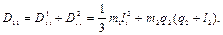

Можно показать, что

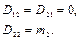
Определим элементы вектора центробежных и кориолисовых сил h, используя выражения (2.33) и (2.34):

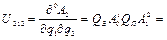
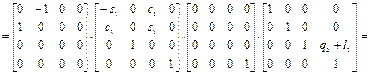
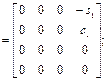
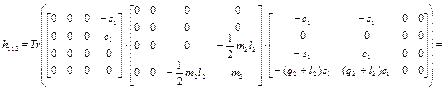
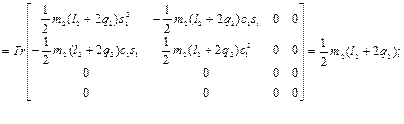
Поскольку

 ,

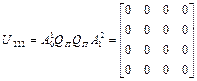то 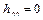 и 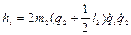. Аналогично можно показать, что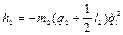

В соответствии с расположением осей базовой системы координат 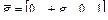, здесь 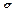=9.8 м/c².

В соответствии с рис.2.5

 ,  .

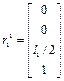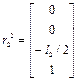Определим элементы вектора гравитационных сил 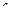, используя выражение (2.35):

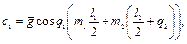
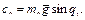
Таким образом, матрица 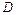 и векторы 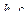, определяющие динамику двухзвенника по выражению (2.29), имеют вид:

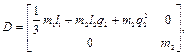
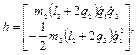                                                               (2.36)

 

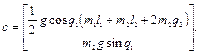
Решение.

Уравнение динамики трехзвенника имеет вид (2.37).

1. Определим коэффициенты матрицы инерции 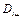, используя выражение (2.39) и (2.40).

Определим вспомогательные матрицы 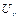 по выражениям (2.40).

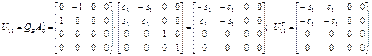
Аналогичным образом имеем:

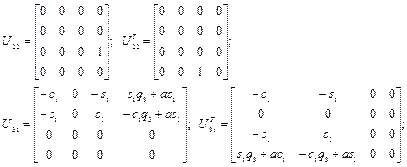
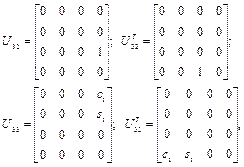
где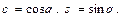

Получим матрицы инерции 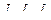 соответствующих звеньев по правилам, изложенным в п. 2.3:

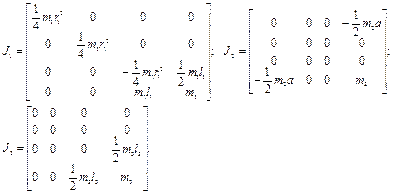
Тогда в соответствии с выражениями (2.39) имеем:

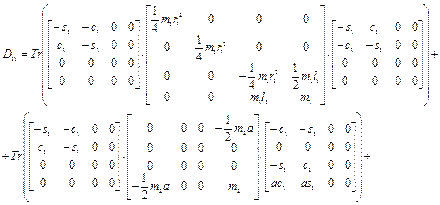
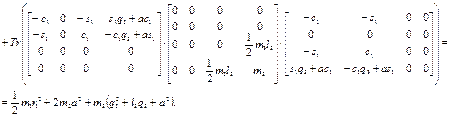
Аналогичным образом имеем:

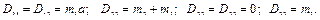
Таким образом, матрица инерции 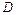 манипулятора имеет вид

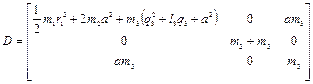. (2.44)

2. Определим элементы вектора 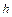 центробежных и кориолисовых сил, используя выражения (2.41). Определим вспомогательные матрицы  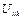по выражениям (2.42).

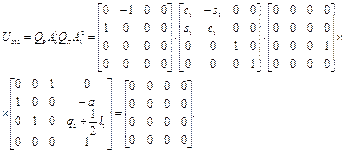
Аналогичным образом имеем:

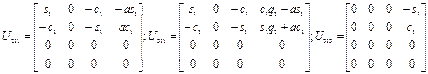
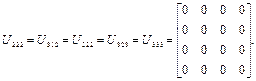
Используем теперь выражения (2.41) для определения элементов .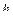

Поскольку матрицы 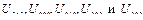являются нулевыми, то соответственно равны нулю и элементы  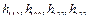в выражении (2.41-а) и следовательно ,

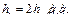где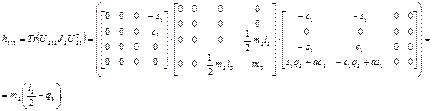

Аналогичным образом можно показать, что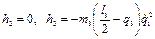

и, соответственно 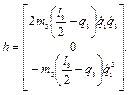                           ………… (2.45)

3. Посредством выражений (2.43), определим элементы 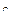 вектора  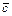гравитационных сил и моментов, действующих в сочленениях рассматриваемого трехзвенника.

В соответствии с расположением осей базовой системы координат 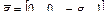, здесь .

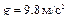В соответствии с рис.1.12 зададим координаты центров тяжести звеньев в связанных с этими звеньями системах координат следующими векторами:

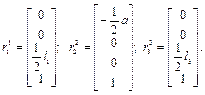
Определим элементы вектора  гравитационных сил и моментов, используя выражение (2.43) и вспомогательные матрицы, полученные в п.1 настоящего решения. В результате имеем:

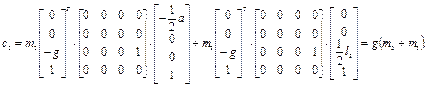
Можно показать, что элементы 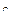 и 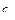 равны нулю, т.е.

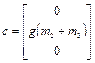.                                       (2.46)

 

Учет двигателей и силового взаимодействия с внешней средой в матмоделях динамики манипуляторов. Уравнение динамики в форме Коши. Динамика манипуляционных роботов в пространстве внешних координат и на многообразиях

В предыдущих параграфах мы рассмотрели процедуры вывода и упрощения математических моделей динамики механической системы манипуляционных роботов. Но, в общем случае, знания этих моделей недостаточно для корректного управления роботом. Необходимо также учитывать динамику исполнительных устройств (двигателей), осуществляющих перемещение звеньев, адекватно описывать силовое взаимодействие робота со средой, представлять динамические модели в удобной для синтеза управлений форме. Рассмотрим эти особенности в описании динамики манипуляционных роботов. 

 

Решение.

В соответствие с решением прямой задачи кинематики для рассматриваемого двузвенника

 

,

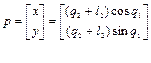запишем матрицу Якоби 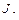, используя выражение (1.40). В результате имеем

.

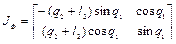Вычислим 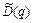как

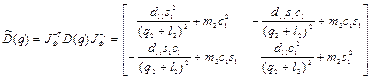, (2.78)

.

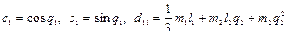С учетом решения обратной задачи кинематики (1.44), (1.45), полученной для рассматриваемого двухзвенника в п.1.9.1, запишем инерционные силы 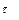в функции внешних координат 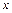и :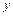

;

 

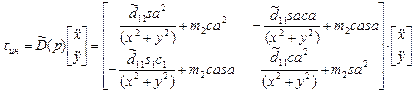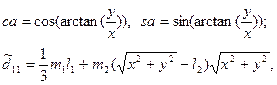
здесь 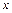, 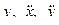- соответственно текущие значения координат положения и ускорений рабочего органа двухзвенника в пространстве внешних координат, которые могут быть определены через решение прямой задачи кинематики (в функции обобщенных координат) или же посредством внешних сенсорных элементов и дополнительных блоков вычисления производных.

 

Кинематические схемы трехзвенных манипуляторов.      Табл.1

Номер варианта	Кинематическая схема	Значение индекса k
1		2
2		3
3		3
4		1
5		2
6		1

 

 

Задание №2. В состав робототехнического комплекса входят два шестизвенных манипуляционных робота МР1 и МР2. Текущее положение рабочего органа МР1, в базовой системе координат, описывается матрицей Т₁, а робота МР2 матрицей Т₂. В соответствии с данными, представленными в табл.2 и заданным вариантом, требуется определить положение рабочего органа МР2 в системе координат рабочего органа МР1.

 

Значения матриц Т₁ и Т₂.                             Табл.2

Номер варианта	Значения матриц Т1 и Т2
1	,
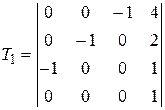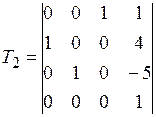
2	,
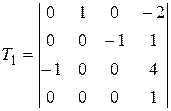3	,
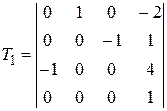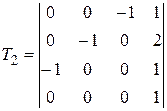
4	,
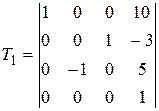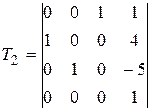
5	,
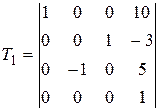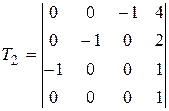
6	,

 

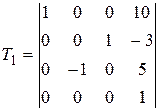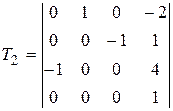
Задание №3. Используя результаты выполнения задания 1, требуется определить следующие элементы уравнения динамики манипуляционного трехзвенника: элементы матрицы инерции D_ij, вектора кориолисовых и центробежных сил и моментов h_s, вектора гравитационных сил и моментов c_l , где значения индексов i , j , s , l определяются по  табл. 3, в соответствии с заданным вариантом.

 

Значения индексов i , j , s , l к заданию №3 .      Табл.3

Индекс	Номер варианта
	1	2	3	4	5	6
i	2	3	2	1	3	1
j	1	2	2	1	3	2
s	3	2	1	3	2	1
l	3	2	1	3	1	3

 

 

Библиографический список

 

1. Попов Е.П., Верещагин А.Ф., Зенкевич С.Л. Манипуляционные роботы. Динамика и алгоритмы.-М.: Наука, 1978.- 400 с.

2. Козырев Ю.Г. Промышленные роботы: Справочник.- М.: Машиностроение, 1983.- 376 с.

3. Фу К., Гонсалес Р., Ли К. Робототехника.- М.: Мир, 1989.-624 с.

4. Denavit J., Hartenberg R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech., 77, p.p. 215-221, 1955.

5. Величенко В.В. Матрично-геометрические методы в механике с приложениями к задачам робототехники. М.. Наука,1988, 288 с.

6. Пшихопов В.Х. Аналитический синтез агрегированных регуляторов манипуляционных роботов// В сборнике РАЕН «Синтез алгоритмов сложных систем», выпуск 9, Москва-Таганрог, 1997, 318 с. С. 93-108.

7. Tchon K., Muszynski R. A normal form solution to the singular inverse kinematic problem for robotic manipulator: the quadratic case. Proc. of the IEEE Inter. Conf. on Robotics and Automation. Leuven, Belgium, 1998, p.p. 3222-3227.

8. Кинематика, динамика и точность механизмов. Справочник./ Под ред. Г.В. Крейнина.- М.:Машиностроение, 1984.- 224 с.

9. Кобринский А.А., Кобринский А.Е. Манипуляционные системы роботов.- М.: Наука, 1985.- 344 с.

10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.- М.: Наука, 1984.- 832 с.

11. Робототехника и гибкие автоматизированные производства. В 9-ти кн. Кн.3. Макаров И.М., Рахманкулов В.З. и др./ Под ред. И.М. Макарова. М.: Высшая школа, 1986.- 159 с.

12. Краснощеков П.С., Петров А.А. Принципы построения моделей. М.: Фазис, 2000.- 412 с

13. Мелентьев Ю.И., Телегин А.И. Динамика манипуляционных систем роботов.- Иркутск: Изд-во Иркутского университета, 1985.- 352 с.

14. Бурдаков С.Ф. Математические модели и дентификация роботов с упругими элементами: Учебное пособие. Л.: Изд-во ЛГТУ, 1990.- 96 с.

15. Уитеккер Э. Аналитическая динамика. - Ижевск: Издательский дом «Ижевский университет», 1999.- 588 с.

16. Краснов М.Л., Кисилев А.И. Макаренко Г.И. и др. Вся высшая математика: Учебник. Т.6.- М.: Едиториал УРСС. 2003.- 256 с.

17. Юревич Е.И. Робототехника: Учебное пособие. СПб.: Изд-во СПбГТУ, 2001.- 300 с.

18. Вукобратович М., Стокич Д., Кирчански Н. Неадаптивное и адаптивное управлении манипуляционными роботами.- М.: Мир,1989. 376 с.

19. Зенкевич С. Л., Ющенко А. С. Управление роботами. Основы управления манипуляционными роботами. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. -399 с.

20.  Шахинпур М. Курс робототехники. М.: Мир, 1990.- 527 с.

21. Пол Р. Моделирование, планирование траекторий и управление движением робота-манипулятора. М.: Наука, 1976.- 104 с.

22. Гайдук А.Р. Алгебраические методы анализа и синтеза систем автоматического управления. Ростов-на-Дону: Изд-во РГУ, 1988.- 208 с.

23. Чаки Ф. Современная теория управления.- М.: Мир, 1975.- 424 с.

24. Филипс Ч., Харбор Р. Системы управления с обратной связью.-М.: Лаборатория базовых знаний. 2001.- 616 с.

25. Pshikhopov V. Kh. New Approach to the Design of the Near Time Optimal Path Following Controller for the Manipulating Robots. Proceedings CD (without pages numbers, 6 pages) and Abstracts Book (473 p., p. 353) of Int. Conf. «Mathematical Theory of Network and Systems», Perpignian, France, June 19-23, 2000.

 

 

Пшихопов Вячеслав Хасанович

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАНИПУЛЯЦИОННЫХ РОБОТОВ

 

 

                                                                                                     Редактор

                                                                                                     Корректор

 

Подписано к печати 

Офсетная печать                    Усл. п.л. – 6,6                  Уч.-изд.л. – 6,2

 

Заказ №                                                      Тираж 500                                        

“С”

 

Издательство

 

 

В.Х. ПШИХОПОВ

 

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАНИПУЛЯЦИОННЫХ РОБОТОВ

 

Учебник

 

 

Учебник представлен в Федеральный институт развития образования, г. Москва, на предмет получения рецензии в соответствии с требованиями Минобрнауки РФ. Копия договора между ТТИ ЮФУ и ФИРО прилагается.

 

Таганрог 2008

УДК 621. 865

 

В.Х.Пшихопов. Математические модели манипуляционных роботов: Учебник. Таганрог: Изд-во ТТИ ЮФУ, 2008. ____ с.

 

 

Изложены формализованные процедуры вывода математических моделей манипуляционных роботов. Рассмотрены алгоритмы решения задач кинематики разомкнутых кинематических цепей, а также вывода уравнений динамики манипуляторов. Представлены модели динамики манипуляционных роботов в различных пространствах, с учетом двигателей и возможного взаимодействия с внешней средой. Приведены примеры вывода матмоделей. Пособие предназначено для студентов и аспирантов высших учебных заведений.

 

 

Рецензенты:

 

Учебник представлен в Федеральный институт развития образования, г. Москва, на предмет получения рецензии в соответствии с требованиями Минобрнауки РФ. Копия договора между ТТИ ЮФУ и ФИРО прилагается.

 

 

ISBN

 

                                               

 

 

 Ó Пшихопов В.Х., 2008  

 

Содержание

1. Кинематика манипуляционных роботов

1.1. Общие понятия и определения.

1.2. Пространства манипуляционных роботов. Постановка

кинематических задач.

1.2.1. Обобщенные и внешние координаты и их пространства.

1.2.2. Прямая и обратная задачи кинематики.

1.3. Матрицы элементарных и сложных поворотов.

1.3.1. Матрицы элементарных поворотов.

1.3.2. Матрицы сложных поворотов.

1.3.3. Матрица поворота вокруг произвольной оси.

1.3.4. Геометрический смысл матриц поворота.

1.4. Матрицы однородных преобразований.

1.4.1. Однородные координаты и матрицы однородных преобразований.

1.4.2. Геометрический смысл матрицы однородных преобразований.

1.4.3. Матрица композиции однородных преобразований.

1.5. Преобразование Денавита – Хартенберга.

1.6. Решение прямой задачи кинематики (ПЗК).

1.6.1. Построение связанных систем координат.

1.6.2. Определение параметров звеньев.

1.6.3. Определение матрицы манипулятора .

1.6.4.Решение ПЗК.

1.7. Решение ПЗК на примере манипуляционного трехзвенника.

1.8. Применение решений ПЗК в задачах робототехники.

1.8.1. Определение базовых координат по показаниям датчиков обобщенных координат.

1.8.2. Понятие матрицы Якоби для решения ПЗК и вырожденные конфигурации робота.

1.9. Методы и подходы к решению обратной задачи кинематики (ОЗК).

1.9.1. Аналитический подход к решению ОЗК.

1.9.2. Геометрический подход к решению ОЗК.

1.9.3. Численные методы решения ОЗК.

2. Динамика манипуляционных роботов

2.1. Уравнения Лагранжа-Эйлера для голономных систем. Динамика материальной точки.

2.2. Скорость произвольной точки -го звена манипулятора.

2.3. Кинетическая энергия механической системы манипулятора.

2.4. Потенциальная энергия механической системы манипулятора.

2.5. Математическая модель механической системы робота.

2.6. Динамическая модель манипуляционного двухзвенника.

2.7. Определение динамических коэффициентов для манипуляционных трехзвенников.

2.8. Анализ динамических моделей манипуляционных систем.

2.9. Подходы к упрощению динамических моделей манипуляторов.

2.10. Особенности моделей динамики манипуляторов при решении задач управления.

2.10.1. Динамика манипуляционных роботов с учетом двигателей.

2.10.2. Динамика манипуляторов при силовом взаимодействии с внешней средой.

2.10.3. Уравнения динамики в форме Коши.

2.10.4. Динамика манипулятора в пространстве внешних координат.

        2.10.5. Динамика манипуляторов на многообразиях.
Введение

 

По оценкам экспертов ООН в самое ближайшее время нашу цивилизацию ожидает бум в развитии робототехники сродни тому, который имел место в 80-х – 90-х годах прошлого века в области компьютеров и компьютерных технологий. Уже начиная с 2002 года, японская фирма Honda приступила к серийному выпуску антропоморфных (человекоподобных) роботов, предназначенных для использования в социальных программах японского правительства. Бурными темпами развивается микроробототехника (хирургические роботы, микророботы военного назначения и т.д.) и робототехника экстремальных сред (космические и подводные роботы, планетоходы и т.д.). От соревновательных программ в сторону реального производства движется развитие мобильных роботов. Укрепляют свои позиции манипуляционные роботы как основной элемент гибких производственных систем. Другими словами, робототехника вторгается в новые области человеческой деятельности, заменяя человека в рутинных операциях, вредных и агрессивных средах, в военной сфере, в исследовании космического пространства и т.п.

 Очевиден междисциплинарный характер робототехники как интегральной науки. Сегодня ее содержание определяют теория систем и теория управления, теория проектирования проблемно-ориентированных вычислительных систем, теория и аппаратно-программные средства параллельных и распределенных вычислений, систем сбора и обработки информации и т.д.

Какова роль специалистов в области теории управления в бурном процессе развития этой относительно новой отрасли человеческой деятельности? Ответ очевиден: даже при самой современной программно-аппаратной базе невозможно создать эффективное робототехническое устройство, не зная и не используя научных методов и подходов, высокоэффективных структурно-алгоритмических решений, которые предоставляет сегодня современная теория управления.

С другой стороны, подход к задачам управления, и не только роботами, требует наличия определенных этапов в процессе их решения. И первый из них – это вывод корректных математических моделей, с различной степенью адекватности отражающих тот или иной реальный объект или процесс.

В настоящем учебнике на основе формализованных процедур, излагаются подходы к выводу математических моделей манипуляционных роботов.

Какова кинематическая связь или как влияют изменения углов поворота и/или перемещения звеньев манипуляционного робота на координаты положения схвата, лазера или другого рабочего органа робота? И, наоборот: по какой программе нужно осуществлять движение звеньев манипулятора, чтобы его рабочий орган описал заданную траекторию движения? Решение этих вопросов, а также необходимый математический аппарат, изложены в первой главе.

Вторая глава посвящена динамике манипуляционных роботов, т.е. математическому описанию взаимосвязи параметров движения роботов (координаты, скорости, ускорения его звеньев) и сил, и моментов, возникающих при этом в сочленениях манипуляторов, функционирующих в различных пространствах.

Без ответов на эти вопросы, без построения адекватной математической модели роботов реализация систем управления ими не приведет к ожидаемым результатам, желаемому качеству и приемлемой точности отработки спланированных траекторий.

При написании учебника использованы как результаты известного формализма, так и оригинальные разработки автора, поясняемые многочисленными примерами.

Настоящий учебник будет полезен не только будущим специалистам в области теории и систем управления, но и всем, кто занимается вопросами проектирования и разработки средств робототехники или сложных механических систем.

Автор хотел бы выразить искреннюю признательность проф. Подураеву Ю.В. (МГТУ «Станкин», г. Москва), проф. Юревичу Е.И., проф. Бурдакову С.Ф. (СПбГТУ, г. С.-Петербург), проф. Манько С.В. и проф. Лохину В.М. (МИРЭА, г. Москва) за благожелательные замечания, послужившие улучшению содержания учебника.