Пусть доход фирмы (домашнего хозяйства) хранится в банке.
На всю хранимую сумму начисляются простые проценты по ставке 100 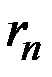 % годовых (
% годовых ( 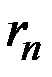 – темп прироста дохода).
– темп прироста дохода).
Для приобретения благ (текущих расходов) фирма регулярно снимает со своего счёта S рублей с интервалами посещения банка (списания с банковской карты) 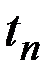 дней.
дней.
За это время все снятые деньги равномерно тратятся.
Снимая в банке необходимую сумму фирма терпит 2 вида издержек:
1) издержки, связанные с посещением банка;
2) издержки, связанные с потерей процентов банка.
Затраты на одно посещение банка не зависят от суммы снятых денег (комиссия по операции, затраты времени и др.) и определяются детерминированной величиной 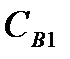 .
.
Издержки, связанные с потерей процентов банка, можно охарактеризовать величиной 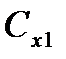 (издержками от хранения единицы денег (одного рубля) в кассе фирмы в течение одного дня)
(издержками от хранения единицы денег (одного рубля) в кассе фирмы в течение одного дня)
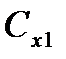 =
= 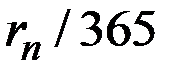 .
.
Обозначим через 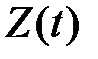 количество наличных денег у фирмы (в кассе) в момент времени
количество наличных денег у фирмы (в кассе) в момент времени 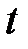 .
.
Предположим, что спрос на деньги (траты) на анализируемый период времени 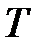 представляет собой детерминированную величину, то есть траты денег в единицу времени (день) осуществляется равномерно с интенсивностью
представляет собой детерминированную величину, то есть траты денег в единицу времени (день) осуществляется равномерно с интенсивностью 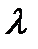 руб./день.
руб./день.
Пусть в начальный момент времени 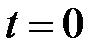 объём наличных денег составлял величину
объём наличных денег составлял величину 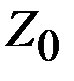 , а их траты за время
, а их траты за время 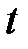 составляют
составляют 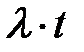 .
.
Уровень наличных денег на любой момент времени 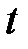 определяется уравнением
определяется уравнением
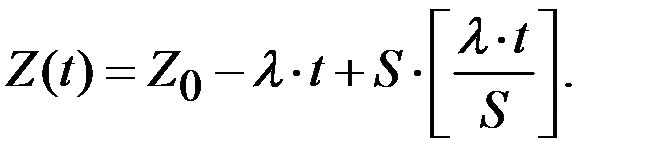
Задача управления наличностью состоит в выборе оптимальной величины суммы (объёма) снятия денег в банке 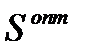 , интервала между посещениями банка
, интервала между посещениями банка 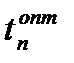 , числа посещений (транзакций)
, числа посещений (транзакций) 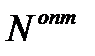 за период
за период 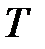 и среднего наличного запаса денег в фирме
и среднего наличного запаса денег в фирме 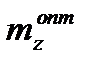 .
.
Критерием оптимальности могут служить суммарные издержки С по управлению наличностью:
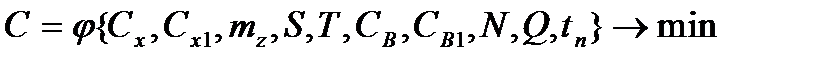 ,
,
где 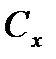 – издержки от хранения денег в кассе фирмы (потеря банковских процентов) за период
– издержки от хранения денег в кассе фирмы (потеря банковских процентов) за период 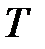 ;
;
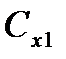 – издержки от хранения единицы денег (одного рубля) в кассе фирмы в течение одного дня (
– издержки от хранения единицы денег (одного рубля) в кассе фирмы в течение одного дня ( 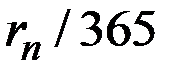 );
);
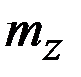 – величина среднего запаса наличности в кассе фирмы;
– величина среднего запаса наличности в кассе фирмы;
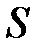 – сумма одного снятия денег в банке;
– сумма одного снятия денег в банке;
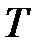 – величина анализируемого периода (дней);
– величина анализируемого периода (дней);
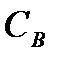 – издержки, связанные с посещениями банка в течение всего анализируемого периода времени Т;
– издержки, связанные с посещениями банка в течение всего анализируемого периода времени Т;
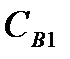 – издержки, связанные с одним посещением банка;
– издержки, связанные с одним посещением банка;
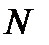 – число посещений банка за анализируемый период;
– число посещений банка за анализируемый период;
 – общий объём снятия денег в банке за анализируемый период Т;
– общий объём снятия денег в банке за анализируемый период Т;
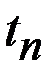 – интервал между посещениями банка.
– интервал между посещениями банка.
Критерий минимизации издержек управления наличностью запишется в виде:
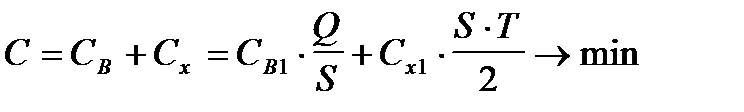 .
.
Исходными данными для решения задачи (неуправляемыми параметрами в целевой функции) являются величины 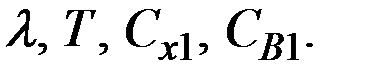
Остальные параметры – управляемые (вычисляемые).
Их оптимальные значения 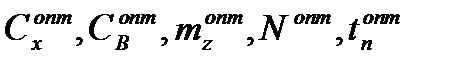 обеспечивают минимум издержек управления наличностью.
обеспечивают минимум издержек управления наличностью.
Пример 9.2. Фирма (домашнее хозяйство) в течение года непрерывно и равномерно тратит (снимая с банковского счёта) 730 тыс. рублей. На всю хранимую сумму начисляются простые проценты по ставке 10% годовых. Издержки, связанные с одним посещением банка, составляют 50 рублей. Определить оптимальную сумму, получаемую при одном посещении банка, оптимальный интервал между посещениями, оптимальные средние издержки в единицу времени (день).
Как изменятся эти характеристики при округлении оптимального интервала между посещениями до целого числа?
Найти характеристики кассы (наличности) при увеличении округлённого до целого интервала времени между посещениями банка в 2 раза.
Решение. Имеются исходные данные:
1) интенсивность трат денег 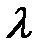 = 2000 руб./день;
= 2000 руб./день;
2) величина анализируемого периода 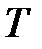 = 365 дней (год);
= 365 дней (год);
3) затраты на разовое снятие денег 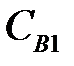 = 50 руб.;
= 50 руб.;
4) издержки от хранения единицы денег (одного рубля) в кассе фирмы в течение одного дня 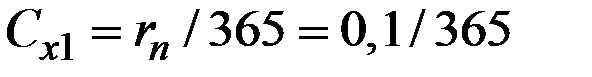 руб.
руб.
Определим оптимальные значения основных величин, определяющих модель управления наличностью, по критерию минимума издержек управления наличностью фирмы.
По исходным данным можно построить график зависимости издержек управления наличностью от размера разовой суммы снятия денег 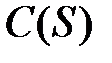 .
.
График получается в результате сложения графиков издержек, связанные с посещениями банка в течение всего анализируемого периода времени Т, и издержек от хранения денег в кассе фирмы (потеря банковских процентов) за этот же период:
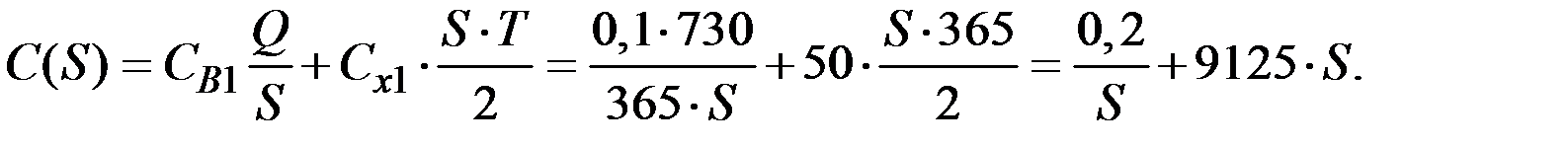
Найдём оптимальные значения искомых величин.
1. Оптимальная сумма при одном посещении банка:
 (рублей).
(рублей).
2. Средний запас налички:
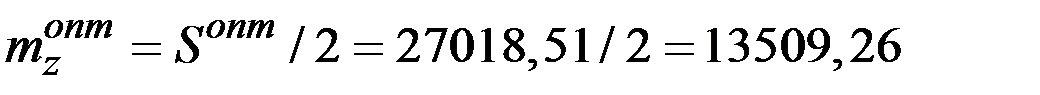 (рублей).
(рублей).
3. Число посещений банка за период 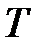 :
:
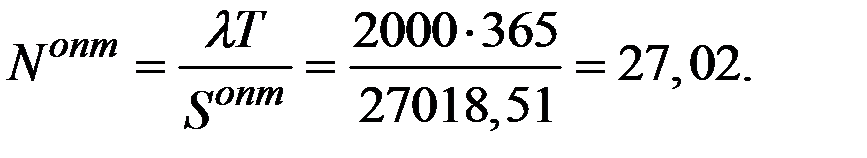
4. Интервал между посещениями банка:
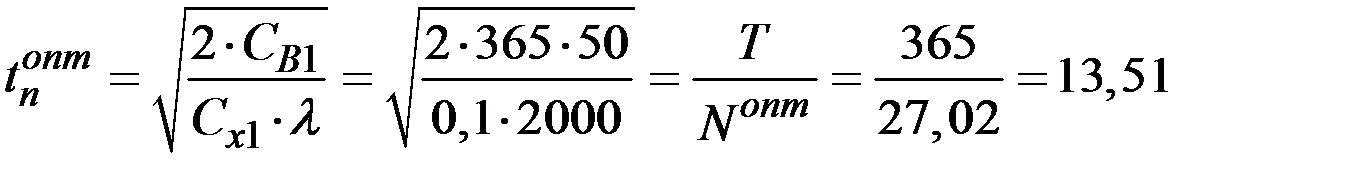 (дней).
(дней).
5. Затраты на снятие налички:
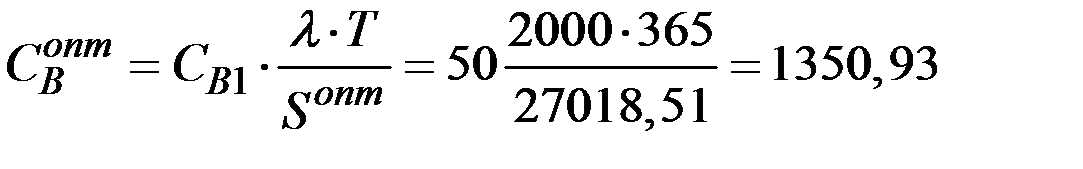 (рублей).
(рублей).
6. Затраты на хранение налички за период 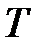 :
:
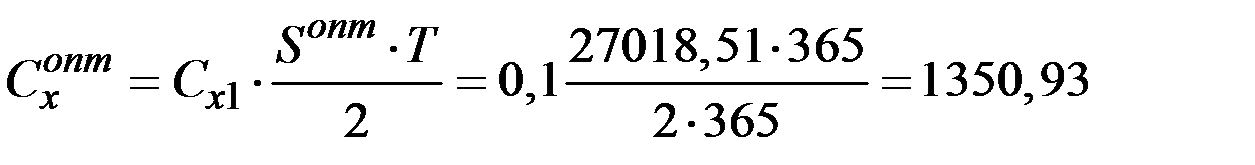 (рублей).
(рублей).
7. Величина общих минимальных издержек:
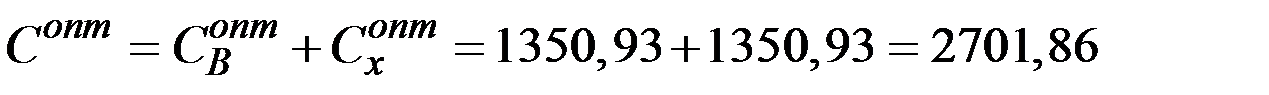 (рублей).
(рублей).
8. Величина удельных (в день) минимальных издержек:
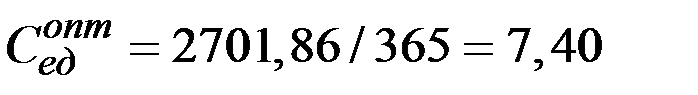 (рублей/день).
(рублей/день).
9. Оптимальные средние издержки в единицу времени можно определить и по другой формуле:
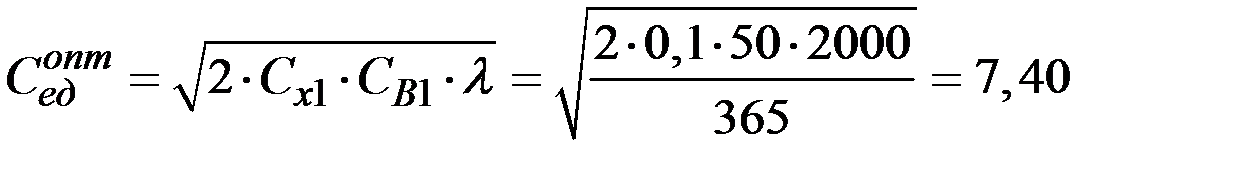 (рублей/день).
(рублей/день).
10. При округлении оптимального интервала между посещениями до 14 дней сумма, получаемая при одном посещении банка, будет равна:
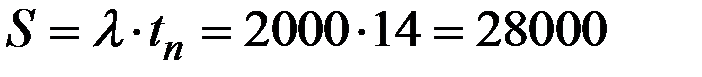 (рублей).
(рублей).
11. Средние издержки на посещение банка и процентные потери в единицу времени определим по формуле:
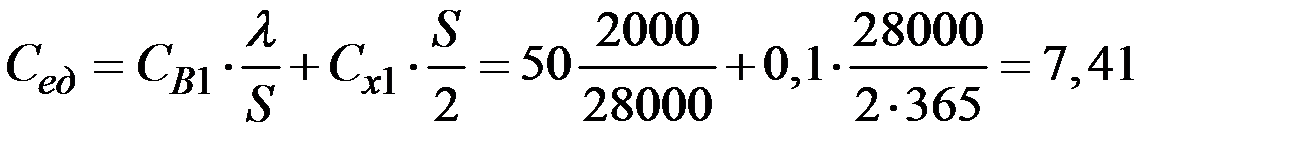 (рублей).
(рублей).
12. При увеличении интервала времени между посещениями банка в 2 раза до 28 дней, сумма, получаемая при одном посещении, составит:
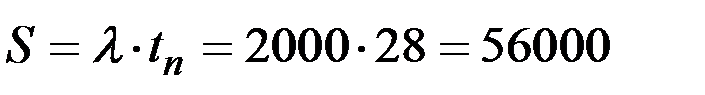 (рублей).
(рублей).
13. Средние издержки на посещение банка и процентные потери в единицу времени будут равны:
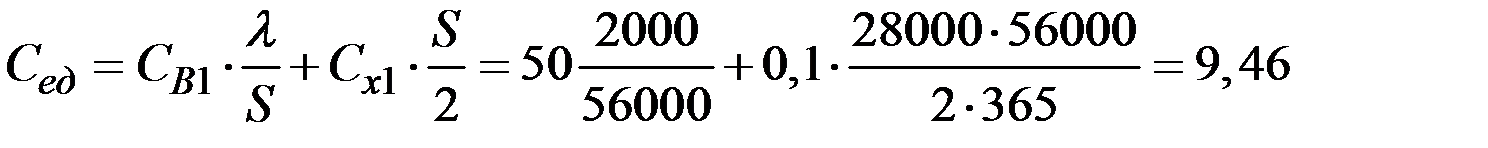 (рублей).
(рублей).
В этом случае средние издержки в единицу времени увеличились на
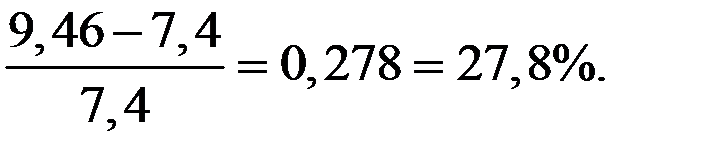
14. Общие издержки на посещение банка и процентные потери:
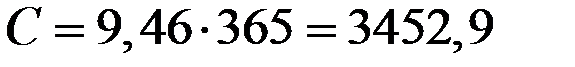 (рублей).
(рублей).
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 9
1. Поясните смысл критерия минимизации издержек обращения.
2. Поясните особенности модели расчёта оптимальных параметров системы управления однономенклатурными запасами.
3. Какие используются приёмы и механизмы управления товарными запасами различных групп товаров?
4. Охарактеризуйте особенности постановки и решения задач управления запасами.
5. Написать уравнение и построить типовой график уровня товарных запасов на любой момент времени t.
Задание 9.1. По имеющимся исходным данным (интенсивность продажи товаров 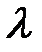 тн./день; величина анализируемого периода
тн./день; величина анализируемого периода 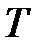 , дней; затраты на ввоз одной партии товара
, дней; затраты на ввоз одной партии товара 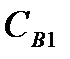 , руб.; затраты на хранение единицы товара (тонны) в течение одного дня
, руб.; затраты на хранение единицы товара (тонны) в течение одного дня 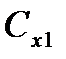 , руб.) определить оптимальные значения основных величин, определяющих модель управления товарными запасами, по критерию минимума издержек обращения.
, руб.) определить оптимальные значения основных величин, определяющих модель управления товарными запасами, по критерию минимума издержек обращения.
Необходимо:
1. Составить критерий минимизации издержек обращения при управлении товарными запасами.
2. Построить график зависимости издержек обращения от размера партии поставок.
3. Найти оптимальные значения величин:
– затраты на ввоз и хранение товаров за период 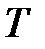 ;
;
– размер одной партии поставки товара;
– число поставок за анализируемый период;
– интервал поставок.
3. Скорректировать полученные характеристики при округлении оптимального интервала поставок до целего и увеличения его в 2 раза.
4. Написать уравнение и построить график уровня товарных запасов на любой момент времени t.
5. Проанализировать полученные результаты.
Варианты заданий приведены в табл. 9.1.
Таблица 9.1
Варианты исходных данных
| № вари– анта | Интенсив–
ность продажи товаров 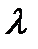 , тн./день , тн./день
| Величина анализируемого периода Т, дней | Затраты на ввоз одной партии товара 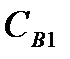 , руб. , руб.
| Затраты на хранение 1 тн. товара в течение дня 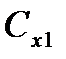 , руб. , руб.
|
| 1 | 2,6 | 440 | 800 | 17 |
| 2 | 1,4 | 420 | 613 | 21 |
| 3 | 2,0 | 360 | ||
| 4 | 3,8 | 750 | ||
| 5 | 4,5 | 500 | ||
| 6 | 1,5 | 309 | ||
| 7 | 0,9 | 610 | ||
| 8 | 1,5 | 720 | ||
| 9 | 2,0 | 657 | ||
| 10 | 5,0 | 1140 | ||
| 11 | 2,7 | 910 | ||
| 12 | 15,0 | 820 | ||
| 13 | 33 | 744 | ||
| 14 | 1,5 | 640 | ||
| 15 | 2,8 | 511 | ||
| 16 | 5,5 | 424 | ||
| 17 | 1,4 | 715 | ||
| 18 | 2,0 | 512 | ||
| 19 | 3,8 | 325 | ||
| 20 | 4,5 | 415 | ||
| 21 | 1,5 | 630 | ||
| 22 | 0,9 | 510 | ||
| 23 | 1,5 | 620 | ||
| 24 | 1,4 | 715 | ||
| 25 | 2,0 | 612 | ||
| 26 | 3,8 | 425 | ||
| 27 | 4,5 | 125 | ||
| 28 | 1,5 | 430 | ||
| 29 | 2,1 | 228 | ||
| 30 | 2,0 | 365 | 50 | 0,274 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике. – М.: Финансы и статистика, 2000. – 368с.
2. Архипов И.К., Кочетыгов А.А., Юдин С.В. Математические методы в финансовой деятельности. Учебн. пособие. – М.: Издательство «Эконом». 2013. – 133 с.
3. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.
4. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. / Учебн. пособие. – М: Финансы и статистика, 2008. – 432 с.
5. Вишняков Я.Д., Радаев Н.Н. Общая теория рисков. 2–е издание – М.: Издательский центр «Академия», 2008. – 368 с.
6. Воробьев С.А. Модели и методы исследования операций. Учебное пособие. Тула: ТулГУ, 2007. – 148 с.
7. Долматов А.С. Математические методы риск–менеджемнта. – М.: Издательство «Экзамен», 2007. – 319 с.
8. Емельянов В.В., Курейчик В.В., Курейчик В.М. Теория и практика эволюционного моделирования. – М.: ФИЗМАТЛИТ, 2003. – 432 с.
9. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник / Под общ. ред. А.В. Сидоровича; МГУ им. М.В. Ломоносова, Изд–во «Дело и Сервис», 2001. – 368 с.
10. Зудин В.И., Архипов И.К., Кочетыгов А.А. Исследование операций. Экономико–математические методы и модели. Учеб. пособие. Тул. филиал РГТЭУ. – Тула: 2009. – 263 с.
11. Зудин В.И., Кочетыгов А.А., Дорофеева Н.П. Экономико–математи–ческие методы и модели. Учебн. пособие. Тула: Тул. филиал Московск. гос. ун–та коммерции, 1999 г. – 214 с.
12. Ильченко А.Н. Экономико–математические методы / Учебное пособие для вузов. – М: Финансы и статистика, 2006. – 288 с.
13. Исследование систем управления. Учеб. Пособие / Г.А. Родионова; Тул. гос. ун–т. – Тула, 2002. – 135 с.
14. Кобелев Н.Б. Основы имитационного моделирования сложных экономических систем. Учеб. пособие. – М: Дело, 2003. – 336 с.
15. Кочетыгов А.А. Моделирование экономических систем: учеб. пособие / Тула: Изд–во ТулГУ, 2012. – 292 с.
16. Кочетыгов А.А. Математическая статистика. Решение задач с использованием пакета SPSS: Учеб. пособие/Тула: Изд–во ТулГУ, 2011. 156 с.
17. Кочетыгов А.А. Тория вероятностей и математическая статистка. Учеб. пособие. Тула: ТулГУ, 2006. – 320 с.
18. Кочетыгов А.А. Случайные процессы. Учеб. пособие. Тула: ТулГУ, 2000. – 308 с.
19. Кочетыгов А.А., Федосеев А.А. Моделирование портфельных инвестиций. Монография/ Тул. гос. ун–т. – Тула, 2013. – 268 с.
20. Кочетыгов А.А., Толоконников Л.А. Основы эконометрики. Учеб. пособие. – М: ИКЦ «Март», Ростов н/д: Издательский центр «Март». 2007. – 344 с.
21. Красс М.С., Чупрынов Б.П. Основы математики и её приложения в экономическом образовании: Учеб. – 2–е изд., испр. – М.: Дело, 2001. – 688 с.
22. Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики. / Учебн. пособие. СПб: Питер, 2010. – 496 с.
23. Кузнецов Б.Т. Макроэкономика. Учеб. пособие. – М.: МАКС Пресс, 2011. – 458 с.
24. Лотов А.В., Поспелова И.И. Многокритериальные задачи принятия решений: Учеб. пособие. – М.: МАКС Пресс, 2008. – 197 с.
25. Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов: Учеб. пособие – М.: Финансы и статистика, 2003. – 416с.
26. Мажукин В.И., Королева О.Н. Математическое моделирование в экономике. / Учебн. пособие. СПб: Питер, 2006. – 496 с.
27. Макарова С.И. Экономико – математические методы и модели. Уч. пособие. – М.: КНОРУС, 2009. – 240с.
28. Математические модели принятия решений в экономике. Учебн. пособие. – М.: Книжный дом "Университет", Высшая школа, 2002. – 288 с.
29. Мелихов М.Б., Кочетыгов А.А. Моделирование и анализ стохастических процессов в экономике. Учеб. пособие. – М: Изд–во МГУК, 2000. – 363 с.
30. Мельников А.В. Риск–менеджмент: стохастический анализ рисков в экономике финансов и страхования. – М.: Анкил, 2003. – 159 с.
31. Мельников Л.В., Попова Н.В., Скорнякова В.С. Математические методы финансового анализа – М.: Анкил, 2006. – 440 с.
32. Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пособие / А.М. Дубров, Б.А. Лагоша, Е.Ю. Хрусталев, Т.П. Барановская; Под ред. Б.А. Лагоши. –2–е изд., перер. и доп. – М.: Финансы и статистика. 2001. – 224 с.
33. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. – М.: ФИЗМАТЛИТ, 2002. – 176 с.
34. Орлова И.В. Экономико–математические методы и модели. Выполнение расчетов в среде EXCEL / Практикум: Учеб. пособие для вузов. – М.: Финстатинформ, 2000. – 280 с.
35. Розен В.В. Математические модели принятия решений в экономике. Учебное пособие. – Москва: Книжный дом «Университет». Высшая школа. – 2002. – 288 с.
36. Смородинский С.С., Батин Н.В. Оптимизация решений на основе методов и моделей математического программирования. – Минск: БГУИР, 2003. –136с.
37. Тихонов Э.Е.. Методы прогнозирования в условиях рынка: учебное пособие. – Невинномысск, 2006. – 221 с.
38. Федосеев В.В. Экономико–математические методы / Учебное пособие для вузов. – М: Юнити–Дана, 2005. – 304 с.
39. Хачатрян С.Р. Прикладные методы математического моделирования экономических систем. Научно–методич. пособие. – М.: Экзамен, 2002. – 192 с.
40. Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций. 5–е издание. – М.: Издательско–торговая корпорация «Дашков и Ко», 2009. – 880 с.
41. Шикин Е.В., Шикина Г.Е. Исследование операций. Учеб. – М.: ТК Велби, Изд – во Проспект, 2006. – 280 с.
42. Шоломицкий А.Г. Теория риска. Выбор при неопределённости и моделирование риска: учеб. пособие для вузов. – М.: ГУВШЭ, 2005. – 400 с.
Учебное издание
Дата: 2019-03-05, просмотров: 803.