До сих пор предполагалось, что решения принимаются с позиции «объективиста». Это означает что ЛПР, будучи трезвомыслящим человеком, откажется от игры, если ему предложат взамен сумму, равную среднестатистическому выигрышу (ожидаемую денежную оценку игры).
В действительности ЛПР может оказаться «субъективистом» и быть либо чрезмерно осторожным, либо склонным к рискованным решениям.
В любом случае ЛПР принимает решение, стремясь максимизировать ожидаемую полезность.
Полезность наряду с матрицей платежей или матрицей рисков – это ещё один способ измерить привлекательность принимаемых решений.
Полезность – это некоторое число, которое можно сопоставить каждому возможному исходу. Каждое лицо, принимающее решения, имеет свою функцию полезности, которая показывает его предпочтения к тем или иным исходам в зависимости от величины риска.
Функция полезности будет выглядеть по–разному для людей избегающих риск (рискофобы) и людей склонных к риску (рискофилы) (рис. 8.11).
Рис. 8.11. Функция полезности для лиц, избегающих риска (кривая А),
и лиц, склонных к риску (кривая В)
Пусть человеку, имеющему, например, 600 рублей, предлагают сыграть в лотерею, в которой он с вероятностью 50% может выиграть 200 рублей и с вероятностью 50% проиграть 200 рублей.
Человек, не склонный к риску (кривая А рис.8.11), отклонит это предложение, поскольку при выигрыше его функция полезности увеличится на величину 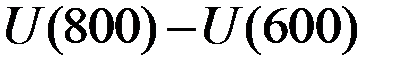 , а при проигрыше его функция полезности уменьшится на величину
, а при проигрыше его функция полезности уменьшится на величину 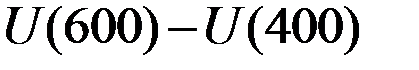 .
.
При этом 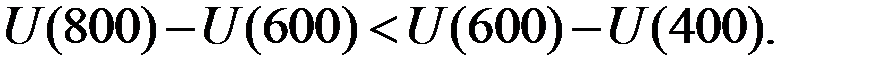
Иначе говоря, ущерб от потери 200 рублей для такого человека существенно больше, нежели удовлетворение от получения 200 рублей (относительная полезность денег убывает и описывается выпуклой вверх функцией полезности).
Для человека, склонному к риску, наоборот, возможность выигрыша 200 рублей является решающим фактором.
Функция полезности в этом случае является выпуклой вниз, и относительная полезность денег растёт при их увеличении (кривая В).
Функцию полезности в теории принятия решений впервые стали использовать американские учёные Дж. Нейман и О. Моргенштерн.
Определить явный вид функции полезности для того или иного ЛПР достаточно сложно. В литературе предлагаются несколько способов определения функции полезности. Самый простой из них, когда известна функциональная зависимость 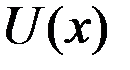 , где U – функция полезности, x– выигрыш. В этом случае индивидуальным является лишь один параметр, который и определяется по склонности ЛПР к риску.
, где U – функция полезности, x– выигрыш. В этом случае индивидуальным является лишь один параметр, который и определяется по склонности ЛПР к риску.
Чаще других за основу берётся экспоненциальная функция.
Например, при анализе решений, связанных с инвестициями, и во многих других бизнес–приложениях используется функция полезности
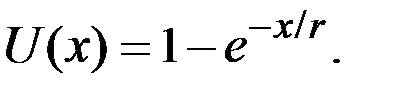
В этой формуле x – денежная сумма, которой мы должны приписать определённое значение полезности, r – определяет меру предрасположенности к риску. Чем больше значение r, тем более компания или индивидуум склонны к риску.
Если событие может иметь несколько исходов, то ожидаемая полезность события равна сумме произведений вероятностей исходов на значение полезности этих исходов:
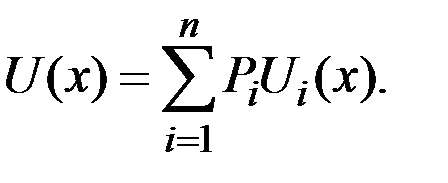
Пример 8.18. Бизнесмен имеет функцию полезности 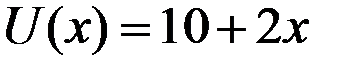 , где x – денежный выигрыш (тыс. долларов). Он может вложить 25 тыс. долларов в строительство бара. С вероятностью 0,5 он потеряет весь свой вложенный капитал и с той же вероятностью выиграет 32 тыс. долларов.
, где x – денежный выигрыш (тыс. долларов). Он может вложить 25 тыс. долларов в строительство бара. С вероятностью 0,5 он потеряет весь свой вложенный капитал и с той же вероятностью выиграет 32 тыс. долларов.
Будет ли бизнесмен инвестировать свой капитал?
Решение. Если не инвестировать капитал (x = 0), то значение функции полезности будет равно
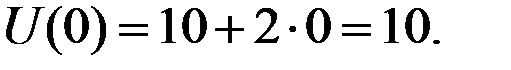
Если инвестировать капитал, то с вероятностью 0,5 денежный выигрыш составит x = – 25, и функция полезности для этого исхода равна
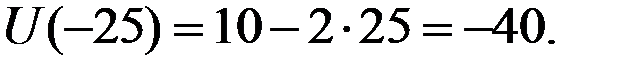
С вероятностью 0,5 выигрыш составит 32 тыс. долларов, а функция полезности для этого исхода равна
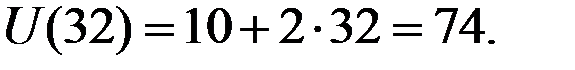
Ожидаемая полезность при инвестировании составит
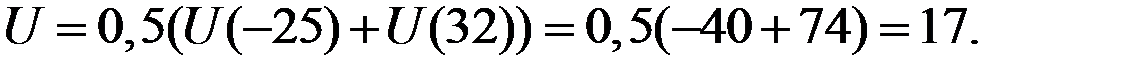
Поскольку полезность инвестирования оказалась выше 10, бизнесмен будет вкладывать капитал в строительство бара.
Пример 8.19. Бизнесмен имеет функцию полезности 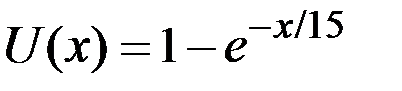 , где x – денежный выигрыш (тыс. долларов). Он может вложить 3 тыс. долларов в строительство кафе. С вероятностью 0,2 он потеряет весь свой капитал и с вероятностью 0,8 выиграет 4 тыс. долларов.
, где x – денежный выигрыш (тыс. долларов). Он может вложить 3 тыс. долларов в строительство кафе. С вероятностью 0,2 он потеряет весь свой капитал и с вероятностью 0,8 выиграет 4 тыс. долларов.
Будет ли бизнесмен инвестировать свой капитал?
Решение. Если не инвестировать капитал (x = 0), то значение функции полезности будет равно
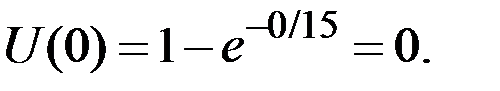
Если инвестировать капитал, то с вероятностью 0,2 денежный выигрыш составит x = – 3, и функция полезности для этого исхода равна
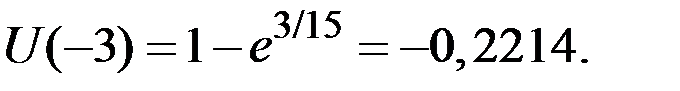
С вероятностью 0,8 выигрыш составит 4 тыс. долларов, а функция полезности для этого исхода равна
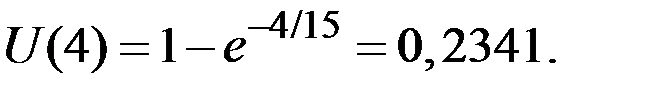
Ожидаемая полезность при инвестировании составит
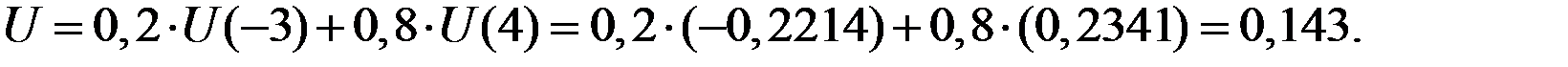
Поскольку полезность инвестирования оказалась положительной, бизнесмен будет вкладывать капитал в строительство кафе.
Пример 8.20. Клиенту фирмы (клуба) предложили выбрать между получением 175 руб. и участием в лотерее, в которой можно выиграть 400 руб. с вероятностью 0,25 и 100 руб. с вероятностью 0,75. Если клиент является рискофобом, то какую альтернативу он выберет? Если предпочтения клиента описываются функцией полезности 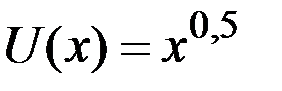 , то чему равен денежный (гарантированный) эквивалент лотереи?
, то чему равен денежный (гарантированный) эквивалент лотереи?
Решение. 1. Клиент–рискофоб предпочитает получение ожидаемого среднего выигрыша лотереи с гарантией (с определённостью), не участвуя в лотерее.
Найдём средний ожидаемый выигрыш:
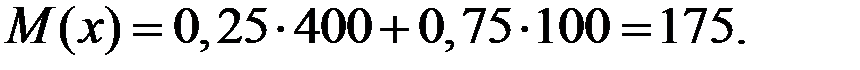
Поскольку ожидаемый средний выигрыш совпадает с гарантированным, то клиент–рискофоб предпочтёт получить 175 руб. с определённостью, т.е. откажется от участия в лотерее.
2. Денежный эквивалент лотереи – это такая сумма денег S, которая приносит агенту полезность, равную ожидаемой полезности лотереи.
Определим эту сумму:
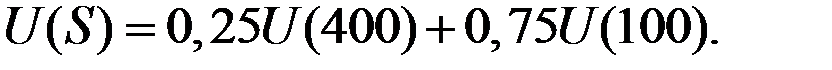
Получаем уравнение
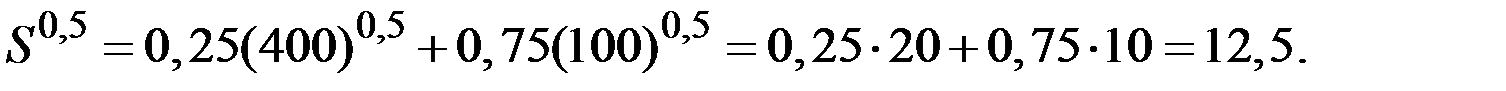
Тогда денежный эквивалент
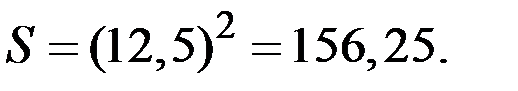
Пример 8.21. Другим двум клиентам клуба предложили участие в этой же лотерее, в которой можно выиграть 400 руб. с вероятностью 0,25 и 100 руб. с вероятностью 0,75. Но их предпочтения описываются, соответственно, функциями полезности 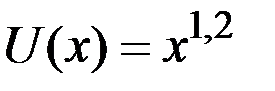 и
и 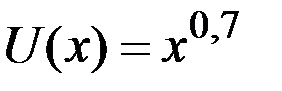 .
.
Определить денежный эквивалент лотереи для этих клиентов.
Решение.
Денежный эквивалент лотереи – это такая сумма денег, которая приносит агенту полезность, равную ожидаемой полезности лотереи.
Эта сумма S определяется выражением:
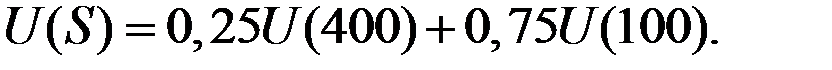
Денежный эквивалент для первого клиента получим из уравнения:
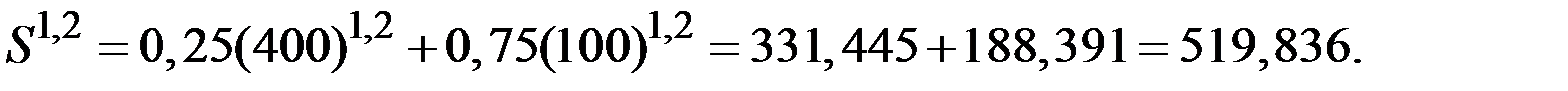
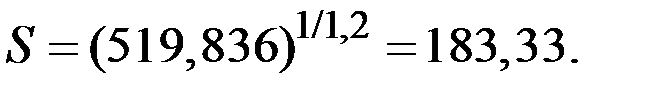
Денежный эквивалент для второго клиента получим из уравнения:
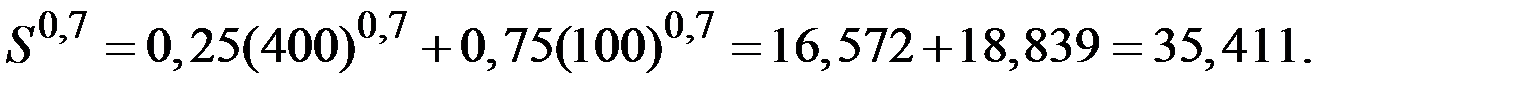
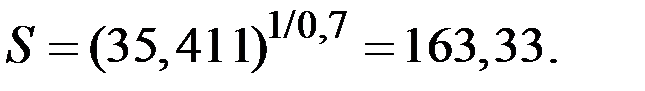
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 8
1. Приведите классификацию игр и поясните их особенности.
2. Что такое минимаксная и максиминная стратегии игроков?
3. Что такое чистая и смешанная стратегии игроков?
4. В чём заключается геометрическое решение игровых задач?
6. Как игры сводятся к задачам линейного программирования?
7. В чём суть проблемы последовательного принятия решения?
8. Как строится и анализируется дерево решений?
Задание 8.1. Исследовать решение трёх игровых задач. Требуется:
1. Найти графическое решение игры № 1 (табл. 8.2).
2. Найти решение игры № 2.
3. Составить двойственную пару задач линейного программирования (прямую и обратную) для игры № 3. Указать возможные пути решения этих задач, их содержательный смысл.
4. Проанализировать результаты. Дать содержательную трактовку (физическую интерпретацию) имеющихся данных и полученных решений.
Варианты заданий приведены в табл. 8.2.
Таблица 8.2
Варианты исходных данных (матрицы платежей)
| № вар. | Игра № 1 | Игра № 2 | Игра № 3 |
| 1 | 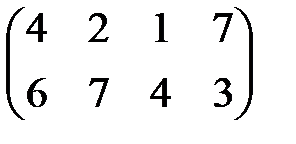
| 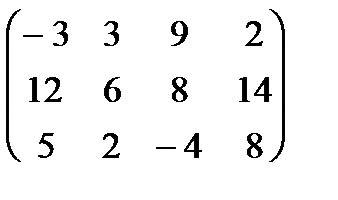
| 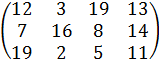
|
| 2 | 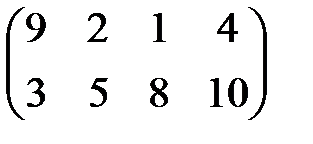
| 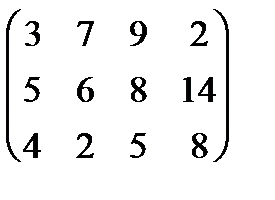
| 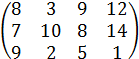
|
| 3 | 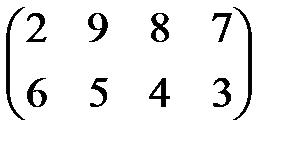
| 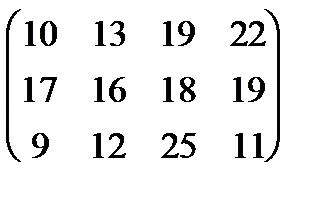
| 
|
| 4 | 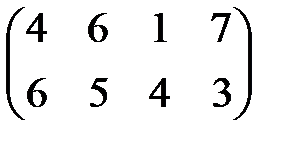
| 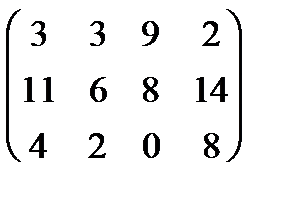
| 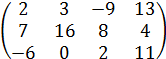
|
| 5 | 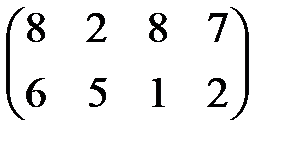
| 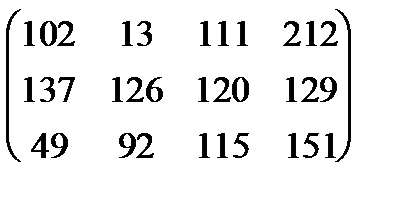
| 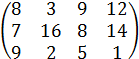
|
| 6 | 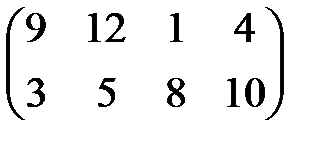
| 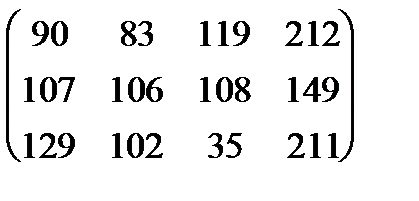
| 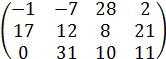
|
| 7 | 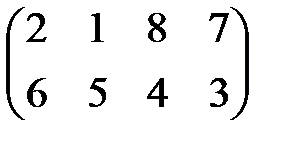
| 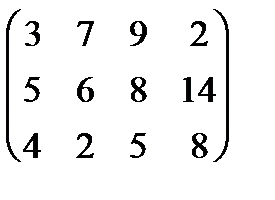
| 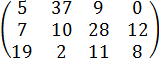
|
| 8 | 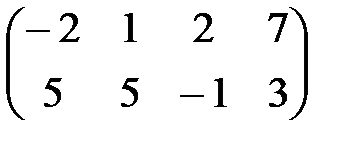
| 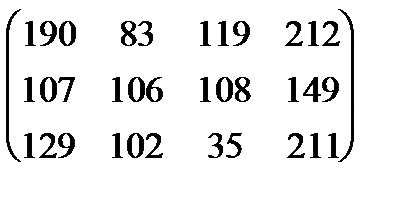
| 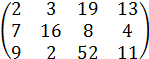
|
| 9 | 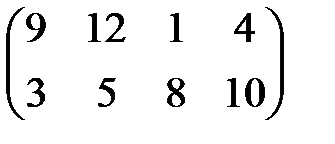
| 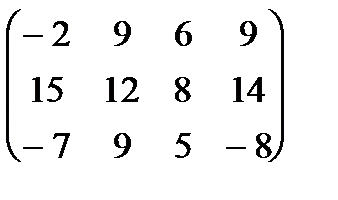
| 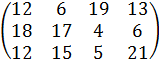
|
| 10 | 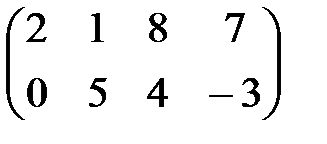
| 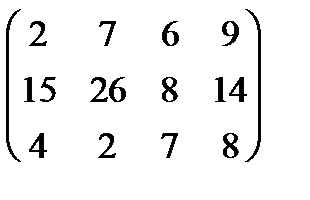
| 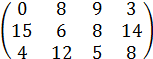
|
| 11 | 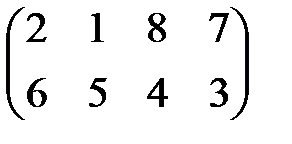
| 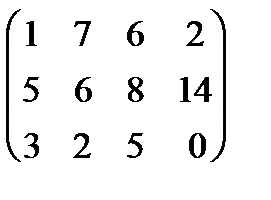
| 
|
| 12 | 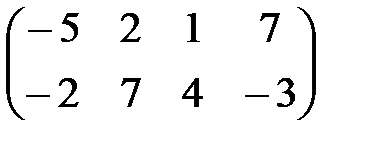
| 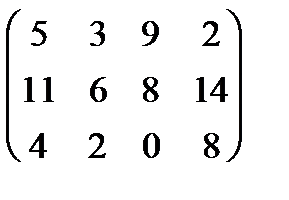
| 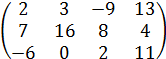
|
| 13 | 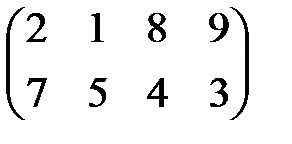
| 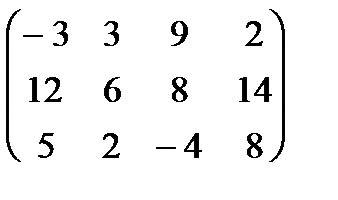
| 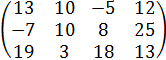
|
| 14 | 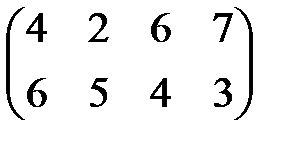
| 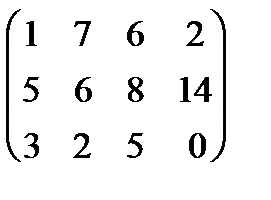
| 
|
| 15 | 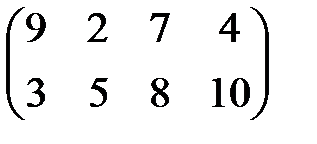
| 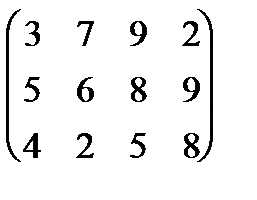
| 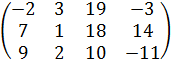
|
| 16 | 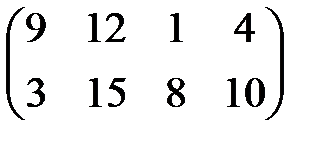
| 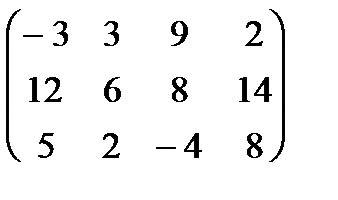
| 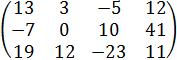
|
| 17 | 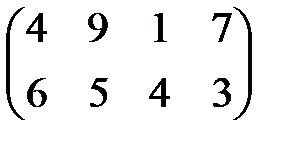
| 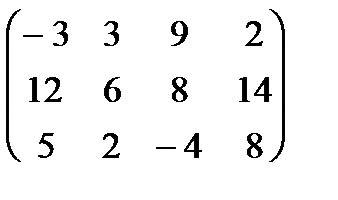
| 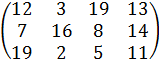
|
| 18 | 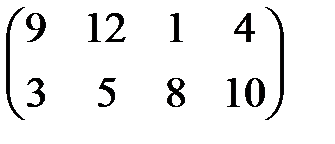
| 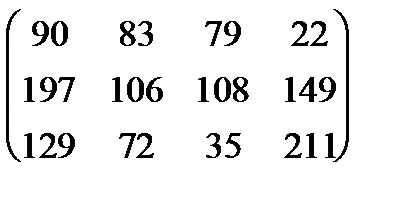
| 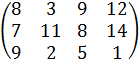
|
Задание 8.2. Фирма рассматривает вопрос о приобретении ценных бумаг (акций) некоторого эмитента.
Если рейтинг рассматриваемых акций возрастает, то такое приобретение окажется фирме выгодным.
Фирма может либо сразу принять решение о покупке пакета акций, либо выполнить (заказать) исследование рынка, что бы лучше оценить относительное правдоподобие повышения или спада рейтинга акций.
Имеем пространство действий фирмы: 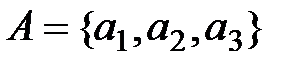 = {изучить рейтинг акций, купить пакет акций, не покупать акции}.
= {изучить рейтинг акций, купить пакет акций, не покупать акции}.
Пространство параметров состояний рынка ценных бумаг: 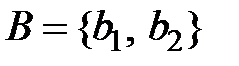 = {рейтинг акций возрос, рейтинг снизился}.
= {рейтинг акций возрос, рейтинг снизился}.
Выборочное пространство обследования рынка ценных бумаг: 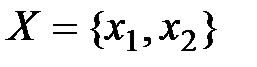 ={прогноз повышения рейтинга акций, прогноз снижения рейтинга акций}.
={прогноз повышения рейтинга акций, прогноз снижения рейтинга акций}.
Вероятности всех неопределённых исходов рассматриваемой задачи приведены в табл. 8.3.
Требуется на основе построения дерева решений проанализировать стратегию действий фирмы и оценить её возможные результаты.
Необходимо:
1. Записать логическую структуру дерева в хронологическом порядке, описывая узлы решений и неопределённость вместе со всеми разветвлениями в каждом узле.
2. Определить вероятность для всех дуг неопределённостей, позаботившись о соответствующих условиях для каждой дуги.
3. Вычислить и приписать значения выигрыша финальным дугам.
4. Двигаясь по дереву справа налево, вычислить математическое ожидание в узлах неопределённостей, максимизировать выигрыш в узлах решений и, таким образом, определить наилучшие действия и их ожидаемые выигрыши.
5. Проанализировать полученные результаты для различных затрат на обследование рейтинга акций.
Таблица 8.3
Варианты исходных данных
| Номер вари– анта | Вероятности исходов
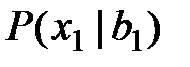
| Вероятности исходов
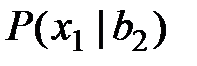
| Вероятности исходов
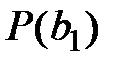
| Сумма средств на покупку акций, тыс.р. | Процент выигрыша при удачной стратегии |
| 1 | 0,75 | 0,48 | 0,65 | 24 | 27 |
| 2 | 0,8 | 0,35 | 0,7 | 13 | 48 |
| 3 | 0,9 | 0,22 | 0,85 | 8 | 56 |
| 4 | 0,75 | 0,48 | 0,65 | 27 | 30 |
| 5 | 0,85 | 0,35 | 0,7 | 53 | 14 |
| 6 | 0,9 | 0,29 | 0,83 | 10 | 35 |
| 7 | 0,82 | 0,22 | 0,65 | 6 | 18 |
| 8 | 0,96 | 0,48 | 0,7 | 70 | 11 |
| 9 | 0,9 | 0,35 | 0,85 | 16 | 53 |
| 10 | 0,75 | 0,27 | 0,65 | 25 | 18 |
| 11 | 0,85 | 0,22 | 0,7 | 15 | 17 |
| 12 | 0,9 | 0,48 | 0,83 | 50 | 45 |
| 13 | 0,82 | 0,35 | 0,65 | 60 | 14 |
| 14 | 0,76 | 0,27 | 0,7 | 35 | 6 |
| 15 | 0,9 | 0,2 | 0,85 | 8 | 40 |
| 16 | 0,75 | 0,38 | 0,65 | 15 | 14 |
| 17 | 0,85 | 0,35 | 0,7 | 13 | 15 |
| 18 | 0,87 | 0,27 | 0,78 | 80 | 8 |
| 19 | 0,82 | 0,25 | 0,65 | 17 | 11 |
| 20 | 0,76 | 0,3 | 0,7 | 23 | 26 |
| 21 | 0,95 | 0,38 | 0,85 | 5 | 50 |
| 22 | 0,92 | 0,35 | 0,65 | 6 | 14 |
| 23 | 0,75 | 0,27 | 0,7 | 7 | 135 |
| 24 | 0,85 | 0,27 | 0,8 | 35 | 48 |
| 25 | 0,9 | 0,24 | 0,65 | 8 | 16 |
| 26 | 0,82 | 0,38 | 0,7 | 15 | 20 |
| 27 | 0,96 | 0,35 | 0,85 | 13 | 19 |
| 28 | 0,88 | 0,27 | 0,65 | 80 | 5 |
| 29 | 0,98 | 0,18 | 0,7 | 1,6 | 28 |
| 30 | 0,97 | 0,33 | 0,83 | 4,5 | 41 |
Дата: 2019-03-05, просмотров: 693.