Если состояниям Природы можно поставить в соответствие вероятности их реализации, найденные статистическим путём или с помощью экспертного заключения, то решение обычно принимается на основании максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска.

Иначе говоря, если для некоторой игры с Природой задана платёжная матрица 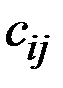, а стратегиям Природы 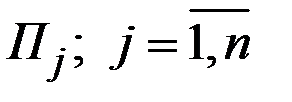, сопоставлены вероятности 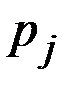, то принимается стратегия игрока 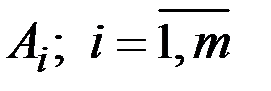, для которой достигается максимальный средний выигрыш

.

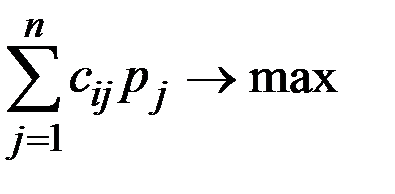Если для построения критерия используется матрица рисков (матрица упущенных выгод) 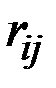, то лучшей будет та стратегия, которая обеспечивает минимальный средний риск: 

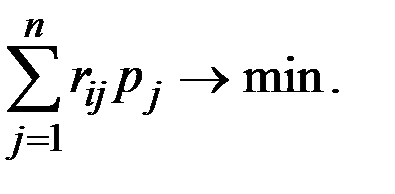
Критерии, основанные на использовании ожидаемого значения выигрыша или ожидаемого риска, целесообразно использовать, когда одно и то же решение приходится применять достаточно большое число раз.

Если решение приходится принимать однократно, то критерии могут привести к ошибочным результатам.

В этом случае необходимо использовать один из вариантов многокритериальной оптимизации, выбирая стратегию, приводящую к максимуму ожидаемого выигрыша и минимальному значению его дисперсии.

Например, можно предложить следующий критерий выбора:

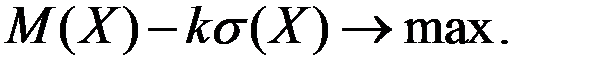
В этой формуле:

M(X) – математическое ожидание некоторой случайной величины X (например, прибыли предприятия),

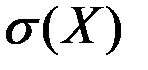 – среднеквадратическое отклонение этой величины,

k – некоторый положительный числовой коэффициент, который учитывает склонность ЛПР к риску при принятии решения.

Чем меньше k, тем больше риск.

Например, предприниматель, очень остро реагирующий на большие колебания прибыли, выберет k достаточно большим, обеспечив выбор стратегии, приводящей к меньшим возможным колебаниям выигрыша.

Пример 8.15. Для доставки свежих фруктов из Краснодара в Москву можно использовать три вида транспорта: A1 – воздушный, A2 – автомобильный, A3 – железнодорожный. Менеджер транспортной компании принял (предположил), что на каждом из видов транспорта могут сложиться три ситуации (благоприятная, нейтральная и неблагоприятная) и рассчитал для этих ситуаций ожидаемую прибыль (доход) компании (млн. руб.). Вероятности реализации благоприятной, нейтральной и неблагоприятной ситуаций на разных видах транспорта, которые менеджер получил на основании данных работы компании за прошлые годы, оказались различными. В таблице ниже приведены величины ожидаемой прибыли (дохода) и вероятности реализации различных состояний транспортной системы (состояний Природы) :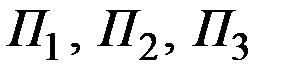

Вид транспорта	Обознач.
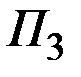
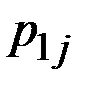
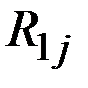
Воздушный		0,6 600	0,39 300	0,01 – 300
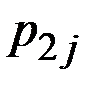
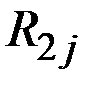
Автомобильный		0,2 450	0,79 300	0,01 – 200
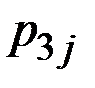
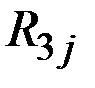
Железнодорожный		0,19 600	0,8 450	0,01 – 100

Какой вид транспорта следует выбрать для доставки фруктов?

Решение. Для принятия решения будем использовать комбинированный критерий максимизации нижней границы гарантированной прибыли (дохода)

,

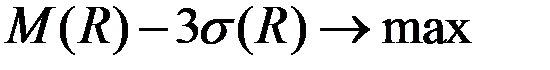полагая значение коэффициента k = 3.

Смысл такого выбора состоит в том, что если случайная величина подчиняется нормальному распределению, то с доверительной вероятностью 0,997 значения этой случайной величины находятся в интервале

.

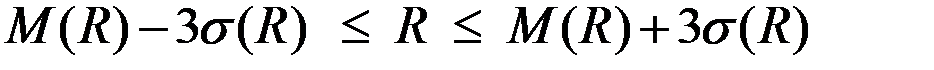Используя в качестве критерия условие максимума величины

,

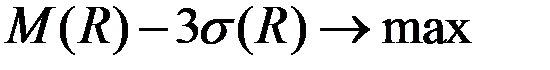мы выбираем стратегию с самым большим минимальным выигрышем.

Найдём средние значения, среднеквадратические отклонения для всех трёх вариантов перевозки по соотношениям:

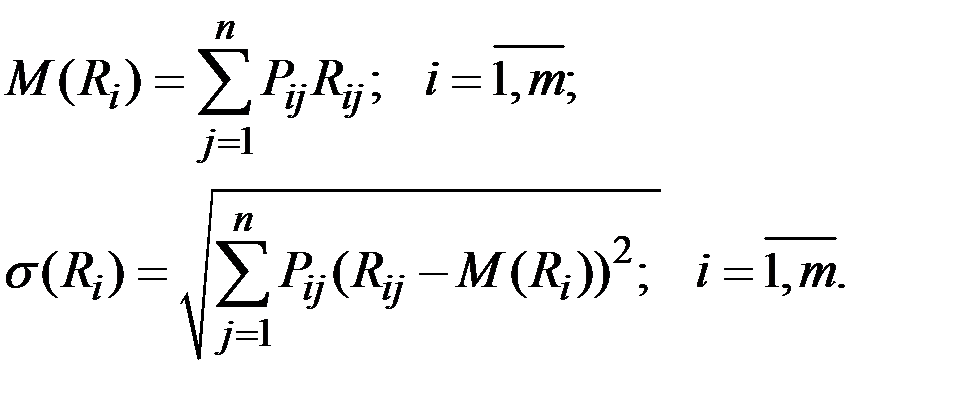
Для удобства эти данные сведены в таблицу, приведённую ниже.

Вид транспорта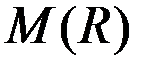
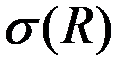
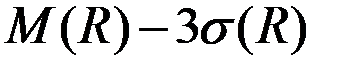
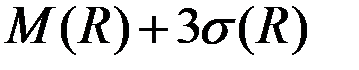
Воздушный	474	165,29	– 21,90	969,90
Автомобильный	325	79,84	85,47	564,53
Железнодорожный	473	82,28	226,14	719,86

Проанализируем представленные в таблице результаты.

Ожидаемое значение прибыли оказалось практически одинаковым для перевозки фруктов воздушным и железнодорожным транспортом, но минимально возможная прибыль существенно выше в случае железнодорожных перевозок (226,14).

Поэтому при принятии решения следует выбрать стратегию перевозки фруктов железной дорогой.

Максимально возможная прибыль выше при перевозке фруктов авиатранспортом (969,9).

Если менеджер склонен к риску и использует принцип «либо пан, либо пропал», то он может ратовать за использование воздушного транспорта.

В связи с рассмотренной задачей остановимся также на проблеме оценки стоимости информации.

Представим себе, что чиновник, контролирующий железнодорожные перевозки, обещает обеспечить самые благоприятные условия перевозки (или знает, что условия будут самые благоприятные), но за эту услугу (информацию) требует определённую плату.

Какова верхняя оценка стоимости такой услуги (информации)?

Очевидно, что в качестве верхней оценки стоимости этой услуги можно взять разность прибыли в условиях полной определённости, когда стратегия однозначно выбрана, и средней статистической прибыли:

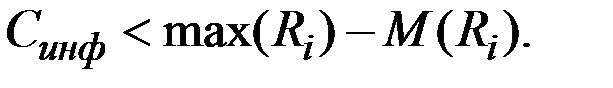
В условиях точного знания, что перевозки железнодорожным транспортом будут проходить в самых оптимальных условиях, прибыль составит 600 млн. руб., а среднестатистическая прибыль равна 473 млн. руб.

Поэтому в качестве верхней оценки стоимости информации о том, что условия перевозки по железной дороге являются наилучшими является разность соответствующих величин:

600 – 473 = 127 (млн. руб.).