В позиционных играх решения формируются в результате многоэтапной процедуры, когда на каждом шаге могут быть свои состояния природы и вероятности их реализации. Решение, принятое на каждом предыдущем шаге, влияет на последующее решение.
Можно сказать, что если имеются два или более последовательных этапов принятия решения, причём последующие решения основываются на предыдущих, и два или более состояний среды, то в этих условиях для принятия решения используется дерево решений.
Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций стратегий и состояний среды.
Следует понимать, что дерево решений – это лишь способ наглядно отобразить существующие стратегии, вероятности состояния природы и выигрыши, соответствующие различным альтернативам.
Предположим следующую ситуацию. На рынке некоторого продукта доминирует производитель–монополист (Фирма 1), и монопольное положение приносит ему 12 млн. руб. прибыли. Высокая прибыль в данном секторе привлекает других производителей.
Фирма 2 решает вопрос: построить ли ей свой завод и начать на нём производство такого же товара? Однако ей известно, что Фирма 1 может предпринять некоторые действия в ответ на вторжение.
С одной стороны, Фирма 1 может снизить объём своего производства, уступая часть рынка Фирме 2 и деля с ней получаемую прибыль.
В этом случае каждая из фирм получит по 6 млн. руб. прибыли.
С другой стороны, Фирма 1 может сохранить объём своего производства. В этом случае рост совокупного предложения товара Фирмами 1 и 2 снизит цену на этот товар, и, как следствие, прибыль Фирмы 1 может снизиться до 5 млн. руб.
Одновременно снижение цен приведёт к тому, что Фирма 2, сделавшая предварительные затраты для выхода на новый для неё рынок, понесёт чистые убытки: она потеряет на этом деле 2 млн. руб.
Если Фирма 2 воздерживается от вступления на рынок, она ничего не выигрывает и не проигрывает, а Фирма 1 продолжает получать монопольную прибыль в 12 млн. руб. Если же Фирма 1 решит в этой ситуации снизить объём своего производства, её прибыль упадёт до 8 млн. руб.
Какое решение принять?
Описанная ситуация может рассматриваться как неантагонистическая игра двух лиц быть и может быть описана следующей матрицей выигрышей (первыми указаны выигрыши Фирмы 1 в млн. руб.):
| Стратегии Фирмы 2 | Стратегии Фирмы 1 | |
| Сохранить объём производства | Снизить объём производства | |
| Выйти на рынок | (5 – 2) | (6 6) |
| Не выходить на рынок | (12 0) | (8 0) |
Данная игра по своим условиям отличается от уже рассмотренных игр. Если ранее мы предполагали, что игроки принимают свои решения одновременно, не зная о решении партнёра, то в данной игре Фирма 1 принимает решение, уже зная о решении, избранном Фирмой 2, что в корне меняет ситуацию.
Игры подобного типа, где задаётся последовательность принятия решений игроками, называются позиционными играми.
Реализация какой из этих двух стратегий наиболее вероятна?
Фирма 2, которая должна сделать первый шаг, при выборе своей стратегии может рассуждать так. "Если мы не вступим на рынок со своей продукцией, то в любом случае мы ничего не потеряем. С другой стороны, если мы решим внедриться на рынок, не исключено, что Фирма 1 сохранит объём своего производства, и для нас это обернётся потерями в 2 млн. руб.!"
Следуя принципу максимизации своего минимального выигрыша, Фирма 2 должна была бы избрать стратегию "Воздержаться от вступления на рынок".
Эти рассуждения не учитывают одной из главных предпосылок теории игр – предположения о рациональном поведении игроков, стремящихся к максимизации своих выигрышей.
В данном случае это заставляет менеджеров Фирмы 2 задать себе вопрос: "А насколько вероятна реализация Фирмой 1 стратегии сохранения объёма производства, если мы вторгнемся на рынок?" Ведь в этом случае Фирма 1 получит меньшую прибыль (5 млн. руб.), чем в случае, если она снизит объём своего производства и поделится частью рынка с нами, получив при этом 6 млн. руб."
В итоге, учитывая, что Фирма 1 будет вести себя рационально, её ответом на вступление Фирмы 2 на рынок должно стать снижение объёма своего производства, а не реализация угрозы сохранить прежний объём производства и подавить Фирму 2.
Проблемы рынка эффективно можно исследовать с помощью построения дерева решений с оценкой возможных результатов в вероятностных терминах.
Задача принятия решения допускает следующую формализацию.
1. Задаётся множество А (пространство действий), которое состоит из всех действий 
, доступных лицу, принимающему решения (ЛПР).
2. Задаётся множество B (пространство параметров), состоящее из всех возможных "состояний Природы" (поведение конкурентов, рыночная ситуация и др.)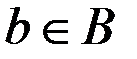 
, из которых реализуется одно и только одно (это истинное состояние Природы неизвестно ЛПР в момент, когда нужно принять решение).
3. Задаётся функция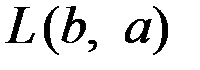 
, называемая функцией потерь с областью определения 
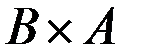(множество всех пар 
, , 
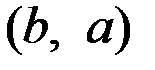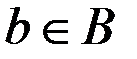) и областью значений R (вещественная прямая); пара 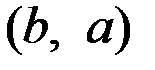называется последствием (от принятия решения a, если истинное состояние природы есть 
).
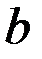4. Наблюдается случайная величина Х, возможные реализации которой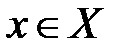 
образуют выборочное пространство X и распределение которой задаётся плотностью распределения вероятностей, принадлежащей заданному семейству 
.
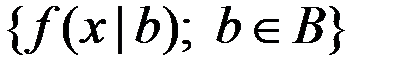5. Определяется множество D, называемое пространством решений и состоящее из всех отображений d множества X в A.
Описанный формализм можно интерпретировать так.
В момент выбора действия ЛПР не знает истинное состояние природы и поэтому ему неизвестны истинные последствия его действия (если ЛПР изберёт действие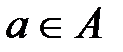 
, то истинное последствие 
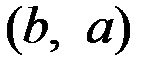неизвестно, поскольку 
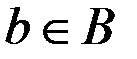неизвестно). Однако ЛПР знает ущерб при каждом возможном последствии 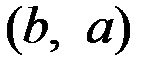, определяемом его выбором действия 
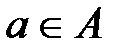и состоянием природы 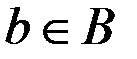(конечно, "ущерб" может быть и "выигрышем"; в этом случае численное значение, приписанное функции 
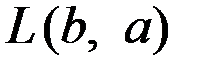, должно быть отрицательным, либо мы можем работать не с функцией потерь, а с функцией выигрыша или полезности).
Чтобы уменьшить неопределённость относительно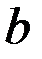 
, ЛПР получает информацию в виде наблюдений случайной величины X, распределение которой зависит от параметра 
.
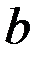Зная, что Х = х, и зная вид плотности распределения вероятностей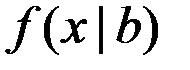 
, ЛПР может извлечь информацию относительно состояния, которая поможет ему в выборе общей стратегии, определяющей выбор для каждого Х = х.
Формально ЛПР выбирает действие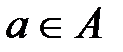 
на основе имеющегося наблюдения 
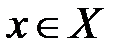. Выбор общей стратегии, определяющей для каждого Х = х действие 
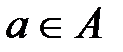, эквивалентен выбору решающей функции 
.
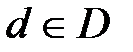Функция d определяет действие, предпринимаемое ЛПР при всех возможных Х = х.
Теорию принятия решений можно считать наукой о том, как выбирать решающую функцию d из пространства решений D.
При оценивании положим A = B (обычно это – вещественная прямая или подмножество прямой), поскольку в данном случае действие состоит в выборе значения параметра (т.е. оценки).
Вид функции потерь зависит от практических особенностей моделируемой задачи, но наиболее типичными являются функции вида
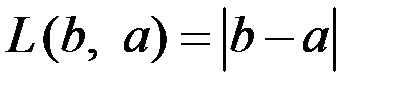или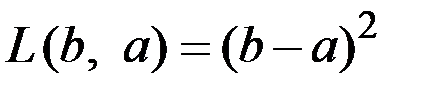 
.
Решающая функция d: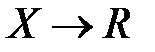 
обычно называется процедурой оценивания, а её значение 
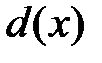является оценкой параметра 
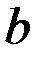по заданным данным Х = х.
При проверке гипотез пространство параметров B представляется в виде двух непересекающихся множеств B0 и B1: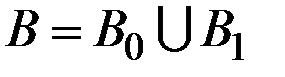 
.
Множество A = {a0, a1} в этом случае содержит всего два элемента, определённые таким образом, что действие a0 состоит в отклонении гипотезы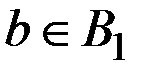 
, а действие a1 – в отклонении гипотезы 
.
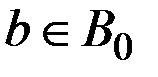Функция потерь зависит от природы множеств B0 и B1.
При проверке простой нулевой гипотезы против простой альтернативной гипотезы пространство параметров также состоит из двух точек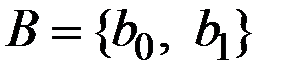 
, и можно, например, положить 
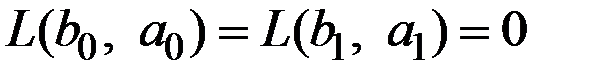(поскольку в этом случае предпринимается правильное действие).
Выбор двух других значени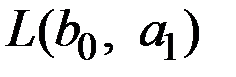й 
и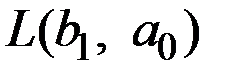 
должен отражать относительную важность ошибок 1 и 2 рода.
Одним из интенсивно развивающихся направлений прикладной статистики является теория последовательного принятия решений.
Рассмотрим задачу.
Предпринимается начальное действие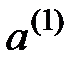 
и после этого Природа оказывается в неопределённом состоянии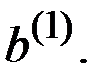 
Затем предпринимается дальнейшее действие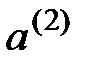 
, приводящее к неопределённому состоянию 
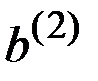, и в итоге получаем последствие 
.
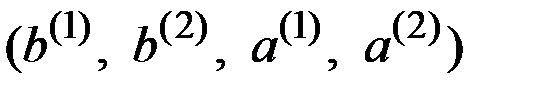Каким образом исследователь должен подходить к задаче выбора начального действия?
Описанная ситуация изображена на рис. 8.3, где квадратами обозначены точки принятия решений (в которых исследователь выбирает действие), а кружками – точки неопределённости (в которых выясняется неконтролируемое состояние Природы).
Предположим, что конечному последствию приписана определённая полезность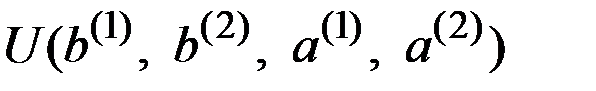 
.
|
|
|
|
|
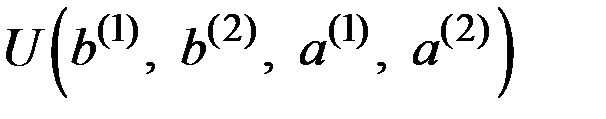
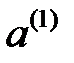
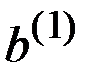
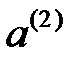
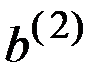
Рис. 8.3. Схема "двухэтапной" последовательной задачи
принятия решений
Конечный веер возможных исходов, исходящий из точки неопределённости, вообще говоря, может быть непрерывным диапазоном как решений, так и исходов.
Суть проблемы последовательного принятия решений состоит в том, что мы не можем разумно решить, что делать на начальной стадии, пока не продумаем все возможные последствия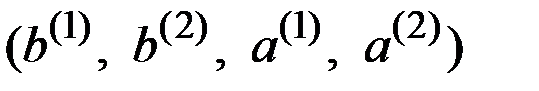 
.
Поэтому мы начинаем с правого конца дерева и спрашиваем, что бы мы хотели сделать во второй точке принятия решений, если первоначально было выбрано действие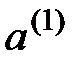 
, а исход оказался 
.
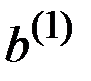Такой подход приводит к дереву, изображённому на рис. 8.4.
|
|
|
|
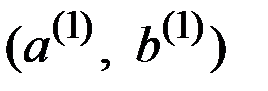
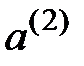
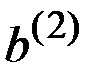
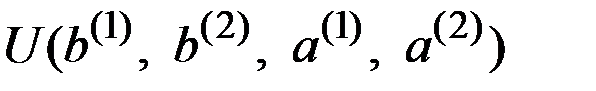
Рис. 8.4. Модификация рис. 8.3 для случая, когда известно, что исходом на начальном этапе является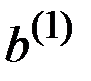 
При данном выборе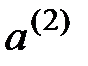 
распределение вероятностей для неизвестного второго исхода 
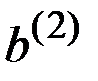имеет вид 
.
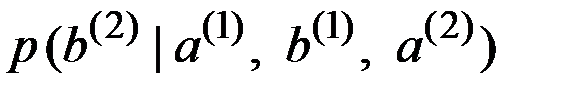Используя для удобства интегральную форму (соответствующую непрерывному диапазону изменения), можно записать условие, определяющее оптимальное действие и ожидаемую полезность, в виде
.
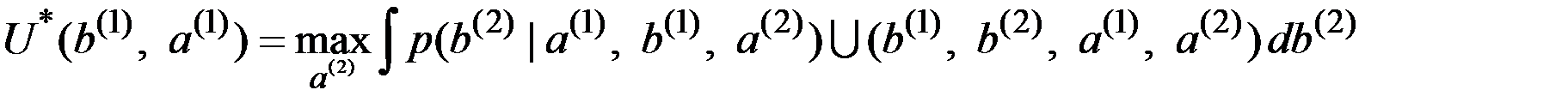Таким образом, для данных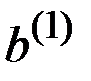 
и 
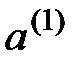определена максимальная полезность.
Ситуацию, с которой исследователь встретился на первом этапе, можно теперь изобразить так, как это показано на рис. 8.5.
|
|
|
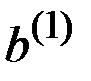
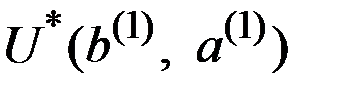
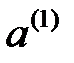
Рис. 8.5. Решение на первом этапе
(в предположении оптимальности решения на втором)
Отсюда видно, что полное решение задачи определяется из условия
.
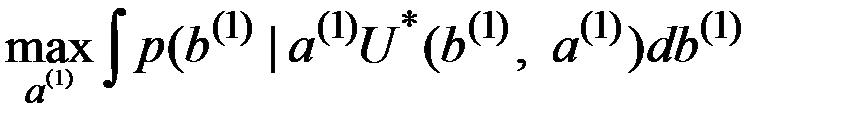Очевидно, что для n–шаговой задачи структура решения остаётся такой же.
Начиная с правой стороны дерева и проходя последовательно через вершины неопределённости и решения, мы будем повторять процедуры взятия математического ожидания и максимизации.
При использовании этой процедуры возникают сложности.
1. Заметим, что в ней неявно используются все возможные "предыстории" процесса (т.е. все комбинации действий, которые можно было предпринять, и исходов, которые могли быть).
2. Распределение вероятностей исходов на данной стадии должно быть условным по отношению к предшествующей истории процесса.
При этом вычисления могут стать очень сложными, если только структура задачи не позволяет упустить возникающие рекуррентные формулы.
В случае конечных множеств действий и исходов задачи могут быть описаны и решены при помощи стандартного простого подхода с использованием дерева решений.
Пример 8.16. Руководство компании решает: 1) создавать ли для выпуска новой продукции новое крупное производство; 2) ограничиться ли строительством малого предприятия; 3) продать патент другой фирме.
Размер выигрыша (прибыль) (тыс. руб.), который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка:
| Стратегия компании | Состояние рынка и вероятности реализации этого состояния р | |||
| Благоприятное |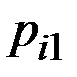 
| Неблагоприятное |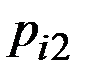 
| |
| Строительство крупного предприятия (1) | 200 | 0,6 | –180 | 0,4 |
| Строительство малого предприятия (2) | 100 | 0,8 | –20 | 0,2 |
| Продажа патента (3) | 28 | 0,7 | 15 | 0,3 |
Какое решение следует принять компании?
Решение. На рис. 8.6 изображено дерево решений, полученное с помощью программного продукта PresionTree7.5. Цифры, которые записаны возле каждой из вершин дерева (на диаграмме они изображены кружками), представляют собой ожидаемый выигрыш для этой вершины.
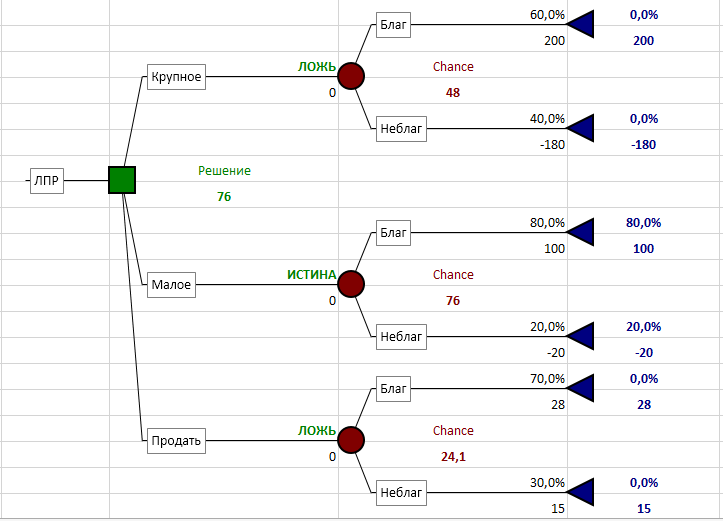
Рис. 8.6. Дерево решений для примера 8.16
Таким образом, в рассмотренном примере следует выбрать стратегию 2, которая даёт наибольший выигрыш:
1) 200∙0,6+(–180) 0,4 = 48; 2) 100∙0,8+(–20) 0,2 = 76; 3) 28∙0,7+15 0,3 = 24,1.
Пример 8.17. Некая компания рассматривает вопрос о капиталовложениях, которые могут оказаться выгодными, если спрос на определённый вид производимой продукции возрастёт, и напрасными, если он упадёт. Компания может либо сразу принять решение, вкладывать ли капитал, либо заказать исследование рынка, чтобы лучше оценить относительное правдоподобие подъёма или падения спроса. Пусть отчёт об исследовании рынка просто содержит прогноз: спрос возрастёт или спрос упадёт, а конечный исход (состояние Природы) можно описать, сказав, что спрос действительно возрос или действительно упал.
Предположим, что прогнозы, выдаваемые фирмой, исследующей рынок, оправдываются на 80% в случае подъёма спроса и на 65% – в случае падения спроса. Предположим, что первоначально (т.е. без дополнительной информации об исследовании рынка) компания считает, что шансы на подъём спроса равны 70%. Предположим также, что если спрос возрастёт, то в результате капиталовложений чистый выигрыш компании составит 163500 (в тысячах рублей), а если спрос упадёт, то 136500. Если же отказаться от капиталовложений, то ожидаемый чистый выигрыш компании составит 150000. Стоимость обследования рынка равна величине С.
Какое решение следует принять компании?
Решение. В ранее принятых обозначениях имеем:
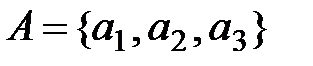(множество действий компании) = {обследовать рынок, вкладывать капитал, не вкладывать капитал};
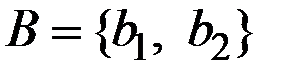(состояние Природы, рыночной среды) = {спрос возрос, спрос упал};
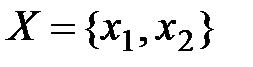(результаты исследования рынка) = {прогноз "подъёма", прогноз "падения"}.
Имеем вероятности событий:
.
.
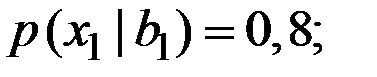
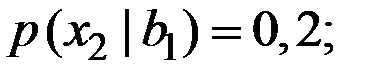
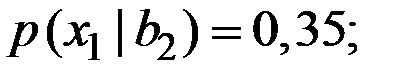
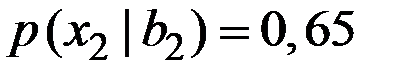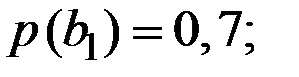
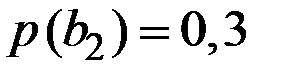Компании нужна прямая оценка вероятностей неопределённого исхода, которую можно получить по формуле полной вероятности, если она закажет исследование рынка. Тогда вероятности подъёма и падения спроса, соответственно, будут равны:
;
.
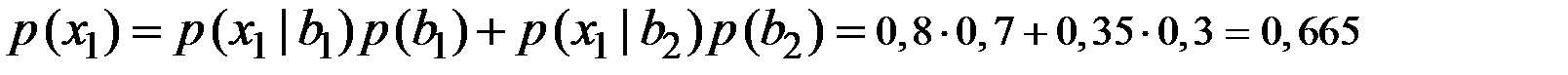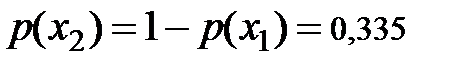Чтобы пересмотреть вероятност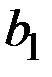и 
и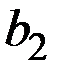 
на основании заданной информации об исследовании рынка, воспользуемся теоремой Байеса
;
;
;
.
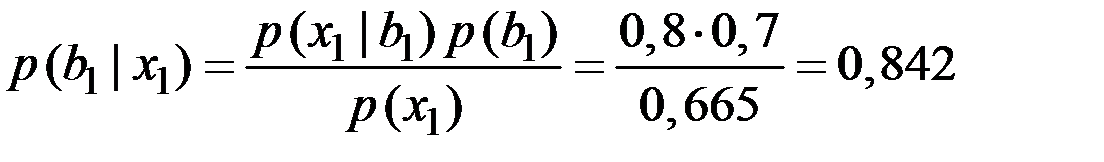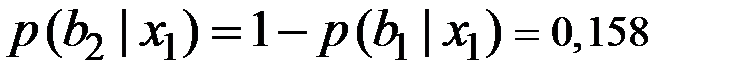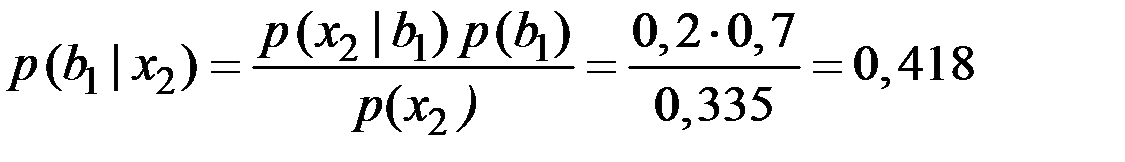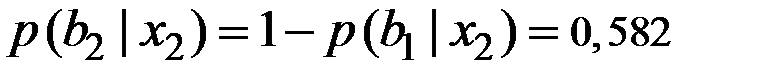Нужно знать полезность различных исходов (рис. 8.7).
| 0,335 |
| 0,665 |
|
|
|
|
|
|
|
|
|
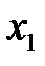
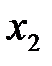
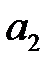
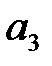
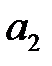
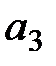
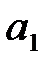
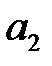
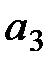
| 0,842 |
| 0,158 |
| 0,842 |
| 0,158 |
| 0,418 |
| 0,582 |
| 0,418 |
| 0,582 |
| 0,7 |
| 0,3 |
| 0,7 |
| 0,3 |
|
|
|
|
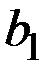
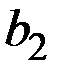
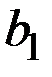
| 150000–С |
| 150000–С |
| 150000–С |
| 150000–С |
| 150000 |
| 150000 |
| 163500–С |
| 136500–С |
| 163500–С |
| 136500–С |
| 163500 |
| 136500 |
Рис. 8.7. Задача о капиталовложениях с вероятностями и доходами
Предположим, что в рассматриваемом диапазоне значений переменных компания считает функцию полезности денег примерно линейной.
На рис. 8.7 показано дерево решений со всей дополнительной числовой информацией. Начиная с правого края дерева, можно вычислить ожидаемые эффекты полезности. Результаты этих вычислений для ветви решения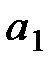 
показаны на рис. 8.8, где, например:
;
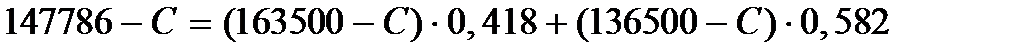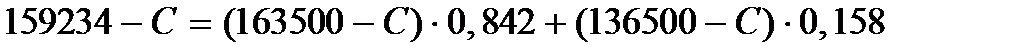
Применяя принцип максимизации ожидаемого выигрыша, мы видим, что при прогнозе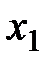 
оптимальным будет действие 
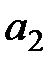, а при прогнозе 
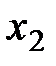оптимальным будет действие 
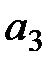. Это приводит к рис. 8.9.
|
|
|
|
|
|
|
|
|
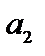
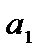
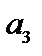
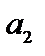
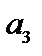
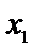
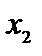
| 0,655 |
| 0,335 |
| 159234 – C |
| 150000 – C |
| 147786 – C |
| 150000 – C |
Рис. 8.8. Первый шаг (вычисление ожидаемого выигрыша) для ветви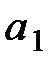 
Вычисляя ожидаемый выигрыш, получим, что для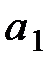 
он равен
.
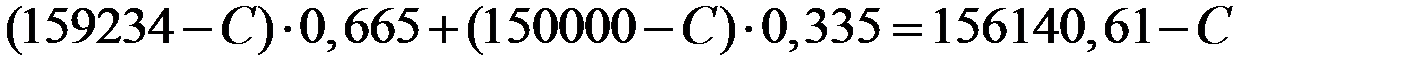Ожидаемые выигрыши для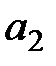 
и 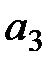составляют соответственно:
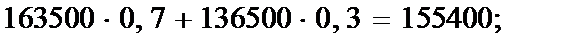
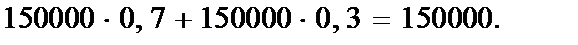
Чтобы выбрать начальное решение следует сравнить ожидаемые выигрыши так, как показано на рис. 8.10.
| 150000 – C |
| 159234 – C |
|
|
|
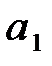
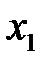
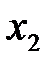
| 0,665 |
| 0,335 |
Рис. 8.9. Второй шаг (максимизация выигрыша) для ветви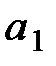 
| 156140,61 – C |
|
|
|
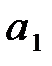
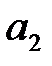
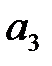
| 155400 |
| 150000 |
Рис. 8.10. Ожидаемые выигрыши при разных исходных действиях
Теперь ясно, что никогда не следует выбирать действие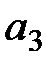 
и что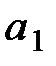 
предпочтительнее, чем 
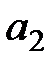, только если плата за исследование рынка не превышает величины 740,61 тыс. руб.
Дата: 2019-03-05, просмотров: 618.
