Методы принятия решений в играх с Природой зависят от характера неопределённости, точнее, от того, известны или нет вероятности различных состояний (стратегий) Природы.
Если вероятности различных состояний Природы неизвестны, то мы имеем дело с принятием решения в условиях неопределённости, а если известны или поддаются оценке, то реализуется ситуация принятия решения в условиях риска.
Допустим, что нам известны возможные состояния (стратегии) природы, но полностью отсутствует информация об их вероятности.
В этих условиях для принятия решения следует составить платёжную матрицу.
Пример 8.12. Рабочий посёлок имеет котельную, которая обеспечивает теплом и горячей водой посёлок зимой. Руководителю поселковой администрации необходимо закупить уголь для работы котельной зимой. Часть угля можно купить в конце лета, поскольку летом он дешевле, а часть зимой. В июне и июле угольный склад не охраняется, и остатки угля с прошлой зимы теряются. Известно, что зима может быть мягкой, средней и суровой, и в зависимости от этого может потребоваться разное количество угля. Глава администрации для трёх своих возможных стратегий рассчитал матрицу выигрышей (млн. руб.).
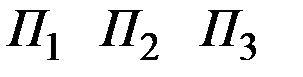
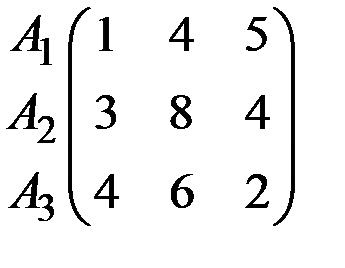
Какую из возможных стратегий должен выбрать глава администрации?
Решение. Рассмотрим на этом примере возможные методики принятия решения в условиях неопределённости.
В ситуации полной неопределённости однозначного решения задачи не существует.
При принятии решения ЛПР может пользоваться одним из возможных критериев:
1) Лапласа, 2) максимакса, 3) Вальда (максимина), 4) Сэвиджа, 5) Гурвица.
1. Критерий Лапласа исходит из предположения, что все стратегии природы равновероятны.
Поскольку в рассматриваемой задачи их три, то вероятность реализации каждой из них может быть принята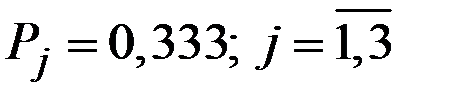 
.
Поэтому ожидаемый выигрыш для каждой из трёх стратегий
.
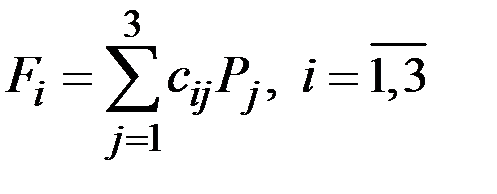Подставляя сюда значения величин выигрышей (коэффициентов)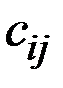 
и вероятности 
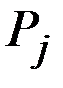, получаем:
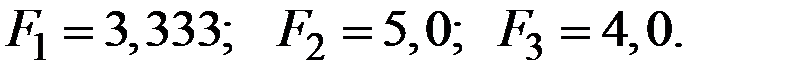
Таким образом, согласно критерию Лапласа, оптимальной получается вторая стратегия, поскольку при этой стратегии ожидаемый выигрыш больше.
2. Критерий максимакса (критерий крайнего оптимизма) исходит из того, что будут реализованы самые благоприятные условия.
Для каждой стратегии игрока выбирается наибольший выигрыш.
Затем из максимальных выигрышей выбирается самый большой.
Этот алгоритм эквивалентен выбору наибольшего элемента матрицы выигрышей.
Очевидно, что согласно этому критерию максимаксный выигрыш составит 8 (вторая стратегия игрока и вторая стратегия природы).
3. Критерий Вальда (максимина, критерий крайнего пессимизма), предполагает, что для каждой стратегии игрока выбирается наименьший выигрыш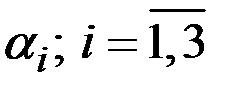 
.
В нашем случае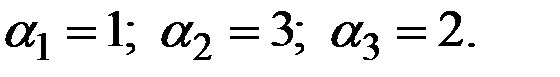 
Затем из найденных худших выигрышей выбирается наибольший.
Это нижняя цена игры с Природой:
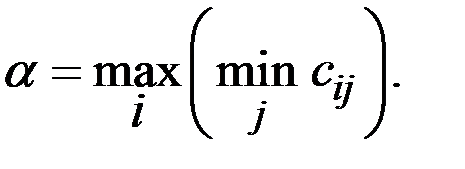
В рассматриваемом случае это будет выигрыш, равный 3 (вторая стратегия игрока).
Этот критерий является критерием крайнего пессимизма, т.к. при оценке выигрыша предполагается, что природа ведёт себя «злонамеренно», реализуя для каждой стратегии игрока наихудшую ситуацию.
4. Критерий минимаксного риска Сэвиджа исходит из анализа матрицы рисков, которая может быть получена из матрицы выигрышей.
Риском игрока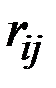 
при выборе им стратегии 
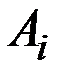и состоянии природы 
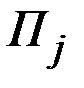можно назвать разность между выигрышем, который мог бы получить игрок, если бы он обладал информацией о состоянии природы, и выигрышем, который он получает согласно матрице платежей.
Рассмотрим первую стратегию игрока и первое состояние природы.
Если бы игрок знал, что реализуется первое состояние природы, то он бы выбрал свою третью стратегию и получил выигрыш 4.
При отсутствии этого знания его выигрыш составит 1.
Таким образом, риск для этой ситуации равен 3.
Можно сформулировать алгоритм получения матрицы рисков из матрицы платежей. В каждом столбце матрицы платежей следует найти максимальный элемент, обозначив его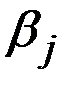 
.
Тогда элементы матрицы рисков равны разности
.
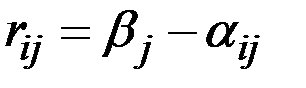Запишем матрицу рисков R для рассматриваемого примера:
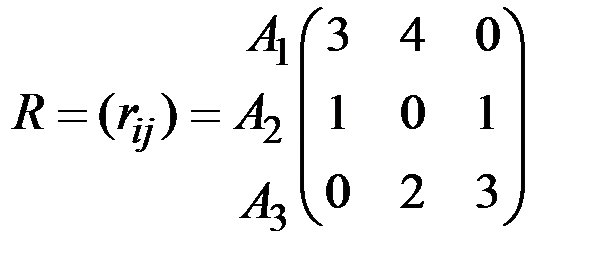
При выборе оптимальной стратегии по критерий минимаксного риска Сэвиджа игрок руководствуется матрицей рисков R:
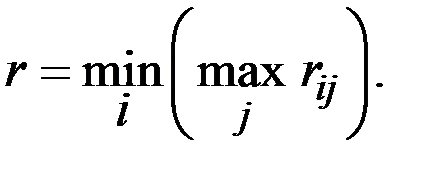
Для нашей матрицы R нетрудно рассчитать:
для стратегии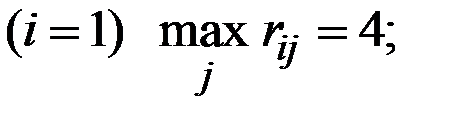 
для второй стратегии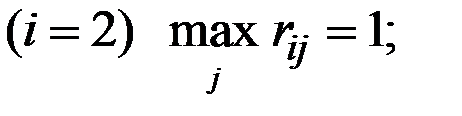 
для третьей стратегии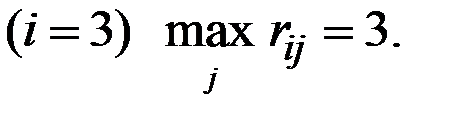 
Минимально возможный из самых крупных рисков, равный 1, достигается при использовании второй стратегии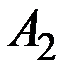 
.
5. Критерий пессимизма – оптимизма Гурвица при выборе стратегии рекомендует пользоваться неким средним результатом, характеризующим состояние между крайним оптимизмом и крайним пессимизмом.
Для каждой стратегии игрока находим величину 
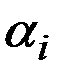по формуле:
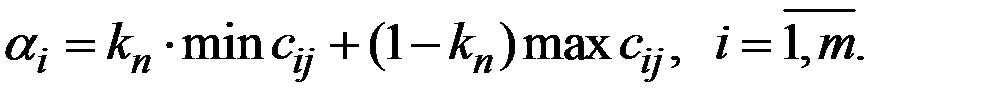
В этом выражении величина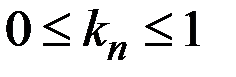 
играет роль показателя пессимизма.
При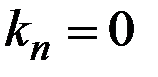 
в строке отыскивается максимальный выигрыш (предельный оптимизм), а при 
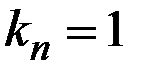– минимальный (предельный пессимизм).
После того как для каждой стратегии величины 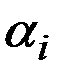найдены, оптимальной считается та стратегия, для которой величина 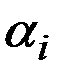максимальна.
Применим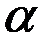 
–критерий Гурвица к платёжной матрице, полагая значение 
.
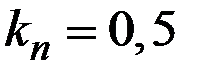Выполняя простые вычисления, получаем:
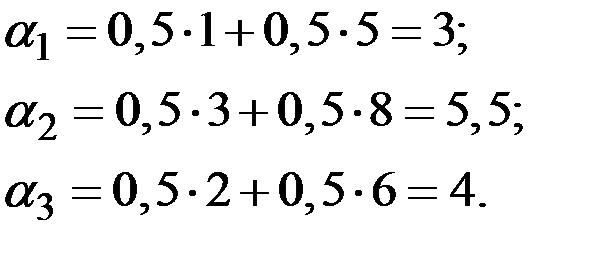
Выбирая максимальное из этих значений, снова приходим к заключению, что оптимальной является вторая стратегия.
Единого подхода к решению задач в условиях неопределённости не существует. Выбор решения остаётся за ЛПР и зависит от его склонности к риску. Тем не менее все испробованные выше стратегии принятия решения в условиях полной неопределённости привели к заключению, что оптимальной при данной матрице платежей является вторая стратегия игрока.
Пример 8.13. Имеется матрица выигрышей
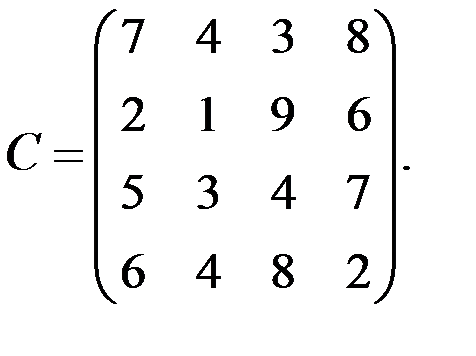
Исследовать решение игры в условиях неопределённости по различным критериям.
Решение. 1. Критерий Лапласа исходит из предположения, что все стратегии природы равновероятны: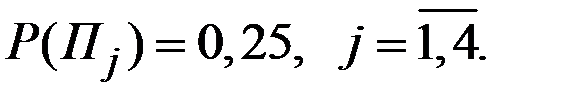 
Ожидаемый выигрыш для каждой из четырёх стратегий игрока:
.
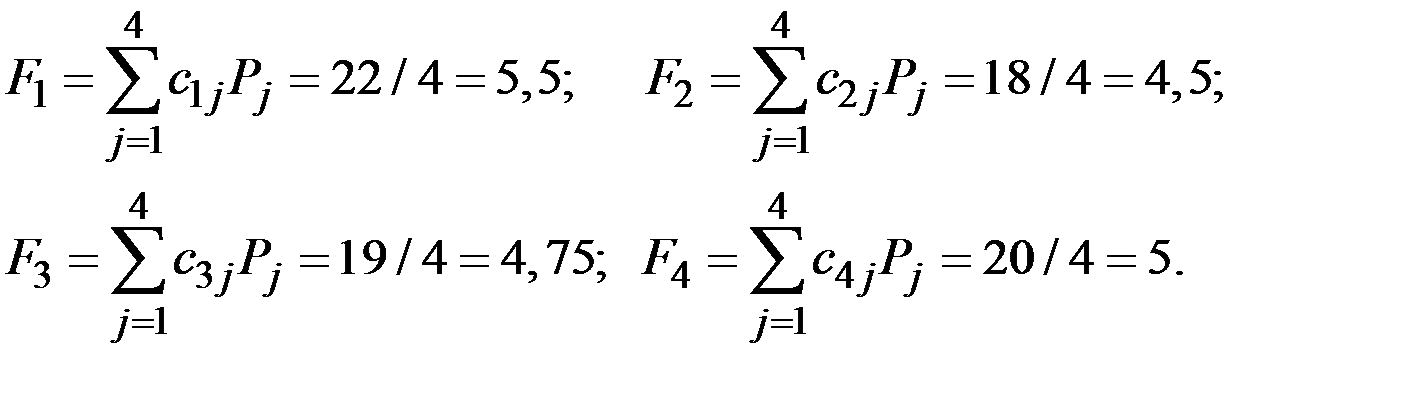Согласно критерию Лапласа, оптимальной получается первая стратегия, поскольку при этой стратегии ожидаемый выигрыш больше.
2. Критерий максимакса (критерий крайнего оптимизма) эквивалентен выбору наибольшего элемента матрицы выигрышей.
Согласно этому критерию максимаксный выигрыш составит 9 (вторая стратегия игрока и третья стратегия Природы).
3. Критерий Вальда (максимина) предполагает, что для каждой стратегии игрока выбирается наименьший выигрыш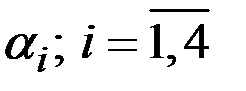 
.
В нашем случае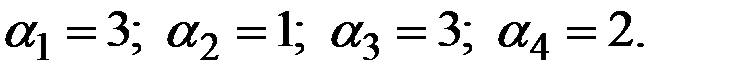 
Затем из найденных худших выигрышей выбирается наибольший.
Это нижняя цена игры с Природой: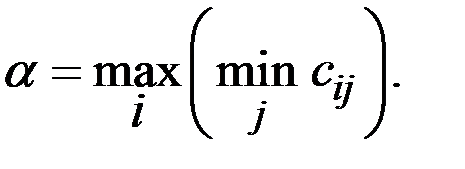
В рассматриваемом случае это будет выигрыш, равный 3 (первая и третья стратегии игрока).
4. Критерий минимаксного риска Сэвиджа исходит из анализа матрицы рисков, которая может быть получена из матрицы выигрышей.
В каждом столбце матрицы платежей следует найти максимальный элемент, обозначив его .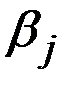
Тогда элементы матрицы рисков равны разности
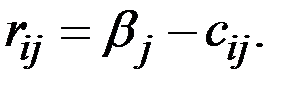
Запишем матрицу рисков R для рассматриваемого примера:
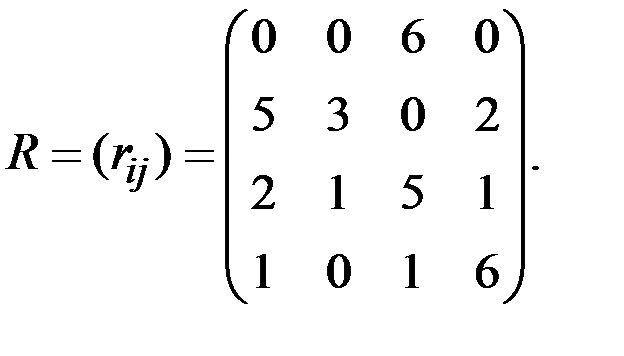
При выборе оптимальной стратегии по критерий минимаксного риска Сэвиджа игрок руководствуется матрицей рисков R:
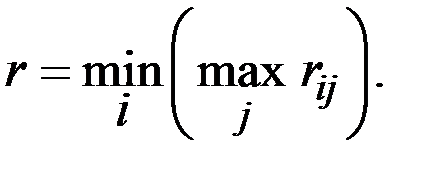
Для нашей матрицы R нетрудно рассчитать:
для стратегии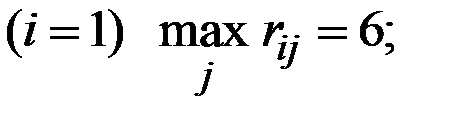 
для второй стратегии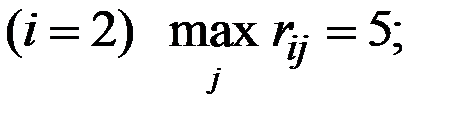 
для третьей стратегии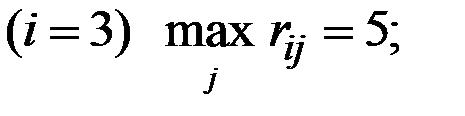 
для четвёртой стратегии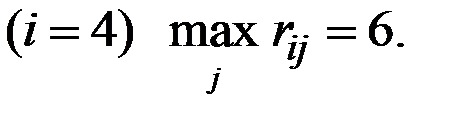 
Минимально возможный из самых крупных рисков, равный 5, достигается при использовании второй и третьей стратеги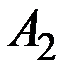й: и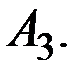 
5. Критерий пессимизма – оптимизма Гурвица при выборе стратегии рекомендует пользоваться неким средним результатом, характеризующим состояние между крайним оптимизмом и крайним пессимизмом.
Для каждой стратегии игрока 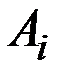находим величину 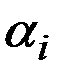по формуле:
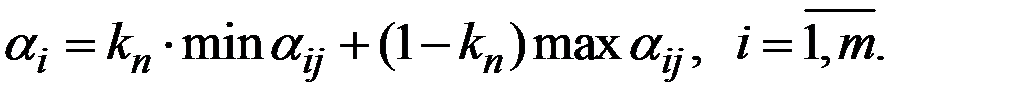
Применим критерий Гурвица к платёжной матрице, полагая значение показателя пессимизма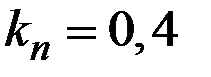 
.
Выполняя простые вычисления, получаем:
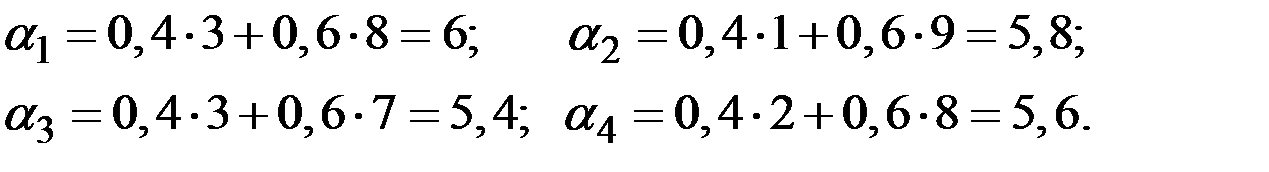
Выбирая максимальное из этих значений, приходим к заключению, что оптимальной является первая стратегия игрока.
Пример 8.14. Возможны 5 планов модернизации производства.
Поэтому потребность в сырье может составлять следующие объёмы: D1 = 2000; D2 = 2500; D3 = 3000; D4 = 3500; D5 = 4000.
Возможны 5 вариантов оборудования склада. Резервы сырья на складе в этих вариантах соответственно могут составлять следующие объёмы: R1 = 2000; R2 = 2500; R3 = 3000; R4 = 3500; R5 = 4000.
Определить оптимальную стратегию управления запасами сырья на складе, если удельные затраты на хранение излишков z1 = 7, удельные издержки дефицитности сырья z2 = 4.
Решение. Могут иметь место следующие стратегии в зависимости от объёмов склады (строки) и потребности в сырье (столбцы):
.
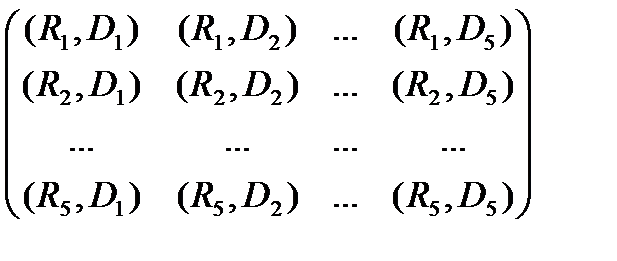Рассчитаем результат каждой стратегии (затраты на хранение излишков сырья и издержки дефицитности сырья):
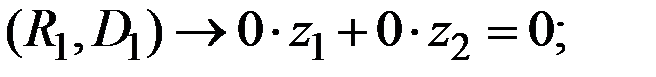
(нет ни излишков, ни дефицитности сырья)
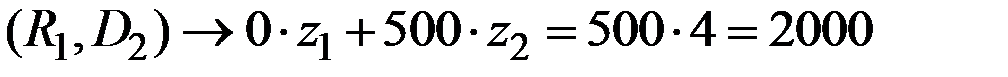
(излишков нет, но есть дефицит сырья в 500 единиц)…
Получаем следующую платёжную матрицу, где элементы означают совокупные издержки по каждой возможной ситуации:
Так как не дано распределение вероятностей для величины потребности, будем считать, что вероятность появления каждой равна 1/5 (всего их пять). Воспользуемся критерием Лапласа.
Рассчитаем затраты по каждому резерву (строке):
CR1 = 4000; CR2 = 3100; CR3 = 3300: CR4 = 4600; CR5 = 7000.
Видим, что использование резерва R2 = 2500 приносит наименьший убыток предприятию величиной 3100.
Дата: 2019-03-05, просмотров: 609.
