Рассмотрим игру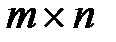 
, определяемую платёжной матрицей
.
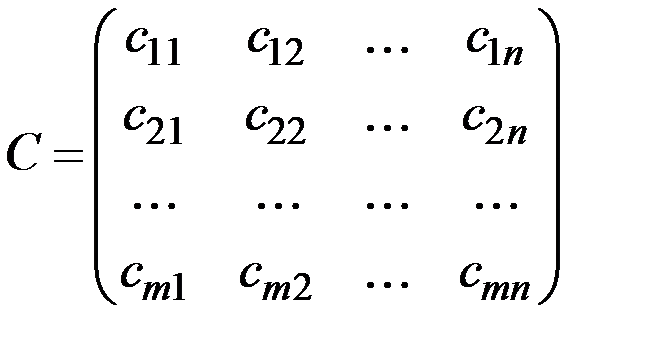Для оптимальной стратегии первого игрока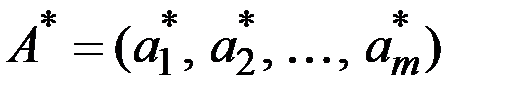 
и цены игры 
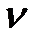выполняется неравенство
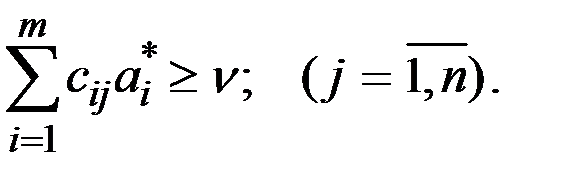
Предположим для определённости, что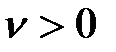 
.
Это всегда может быть достигнуто благодаря тому, что прибавление ко всем элементам матрицы С одного и того же постоянного числа K не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на K.
Разделив теперь обе части последнего неравенства на 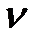, получим
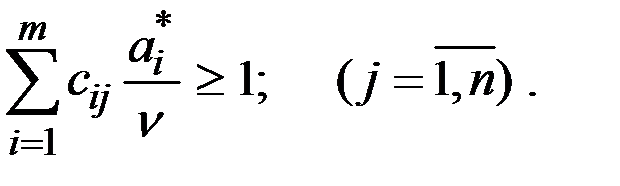
Положим
.
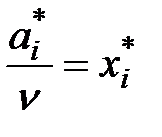Tогда
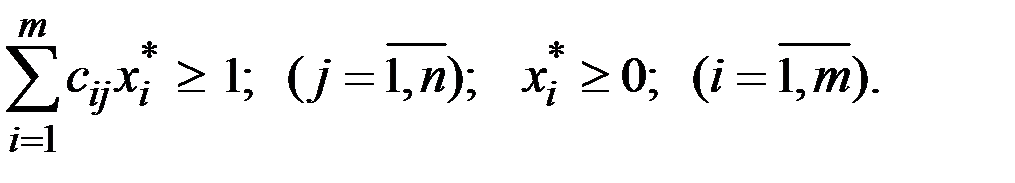
Используя введённое обозначение, перепишем условие
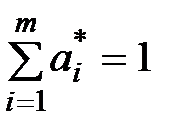
в виде
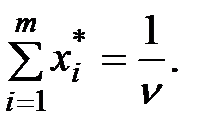
Так как первый игрок стремится получить максимальный выигрыш, то он должен обеспечить минимум величине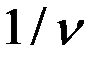 
.
С учётом этого, определение оптимальной стратегии первого игрока сводится к нахождению минимального значения функции
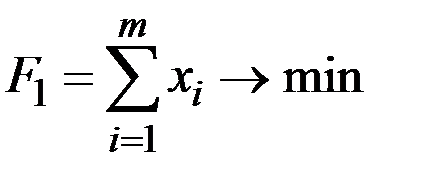
при условиях
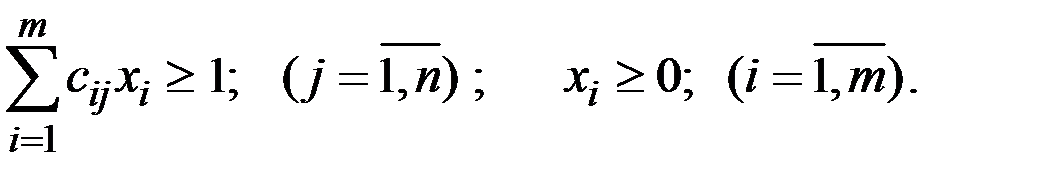
Аналогичные рассуждения показывают, что определение оптимальной стратегии второго игрока сводится к нахождению максимального значения функции
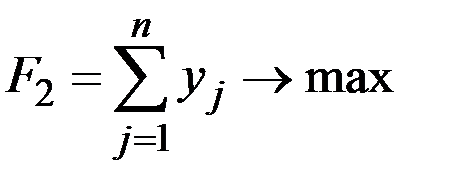
при условиях
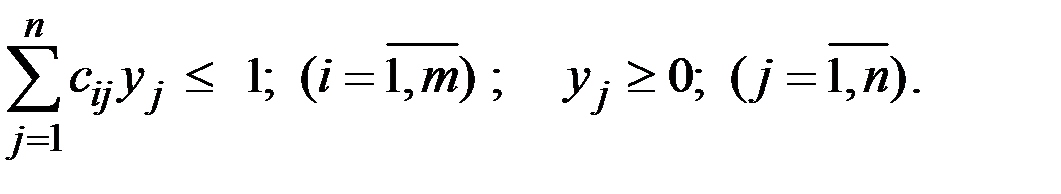
Здесь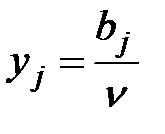 
.
Итак, чтобы найти решение игры, определяемой матрицей С, нужно составить пару двойственных задач и найти их решение:
1. Найти минимальное значение функции
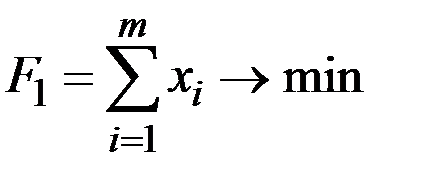
при условиях
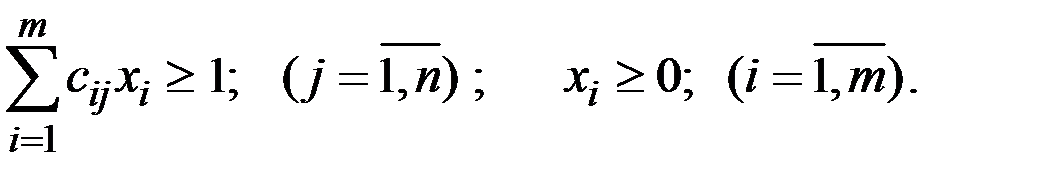
2. Найти максимальное значение функции
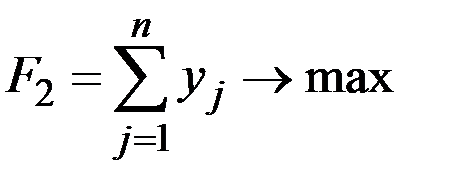
при условиях
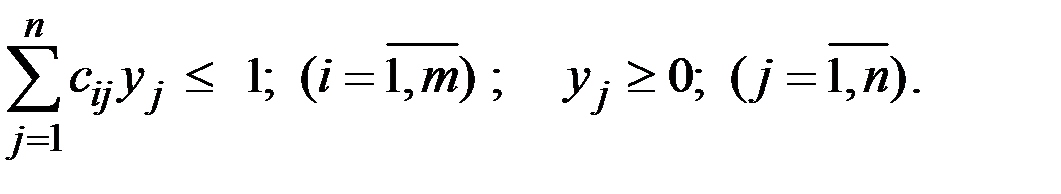
Используя решение пары двойственных задач, получаем формулы для определения стратегий и цены игры:
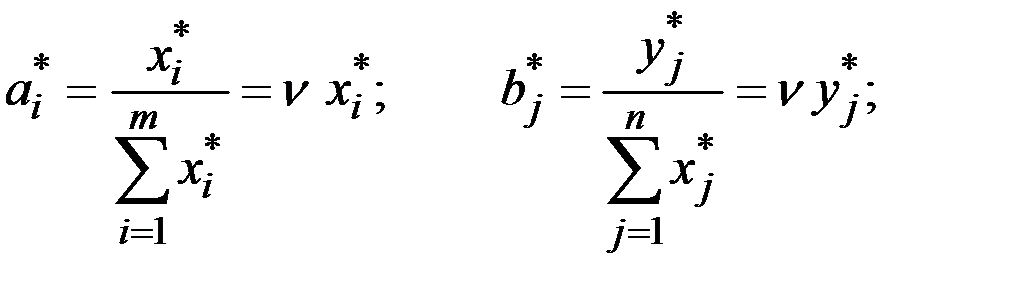
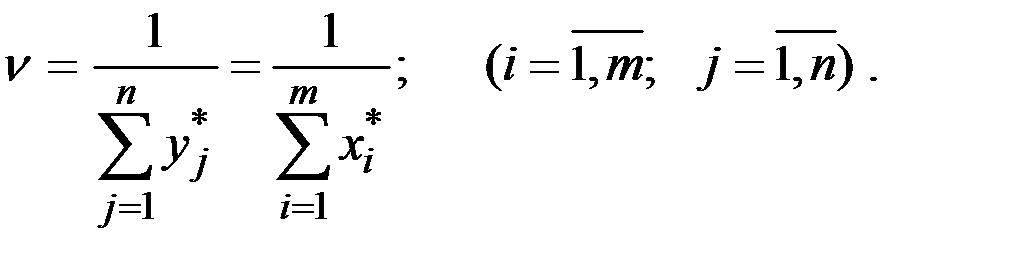
Итак, процесс нахождения решения игры с использованием методов линейного программирования включает следующие этапы:
1. Составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
2. Определяют оптимальные планы пары двойственных задач.
3. Используя соотношение между планами пары двойственных задач и оптимальными стратегиями и ценой игры, находят решение игры.
Пример 8.6. Два игрока А и В одновременно и не сговариваясь показывают один, два или три пальца. Выигрыш решает общее количество пальцев: если оно чётное, то выигрывает А и получит у В сумму, равную этому числу; если нечётное, то, наоборот, А платит В сумму, равную этому числу. Определить стратегии поведения игроков.
Решение. Составим матрицу игры. В каждой партии у каждого игрока три стратегии: показать 1, 2 или 3 пальца.
Поэтому имеем матрицу игры в виде таблицы:
| Стратегии | В1 = 1 | В2 = 2 | В3 = 3 | a i |
| А1 = 1 | 2 | –3 | 4 | –3 |
| А2 = 2 | –3 | 4 | –5 | –5 |
| А3 = 3 | 4 | –5 | 6 | –5 |
| b j | 4 | 4 | 6 |
Здесь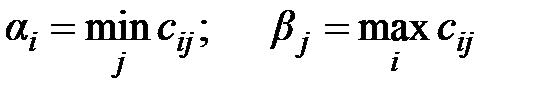 
.
Нижняя цена игры игрока А равна величине
.
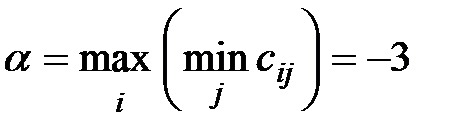Это означает, что при разумном, осторожном поведении мы гарнируем, что не проиграем больше, чем 3.
Нижняя цена игры игрока В (верхняя цена игры для игрока А)
.
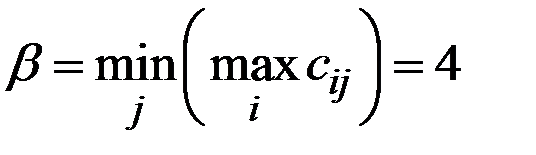Оптимальные стратегии игроков возможны в смешанных стратегиях
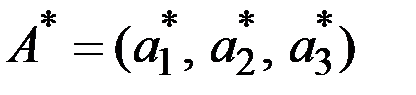и 
.
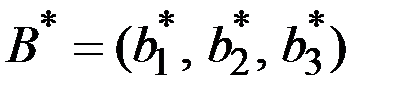Для оптимальных стратегий имеем соотношения:
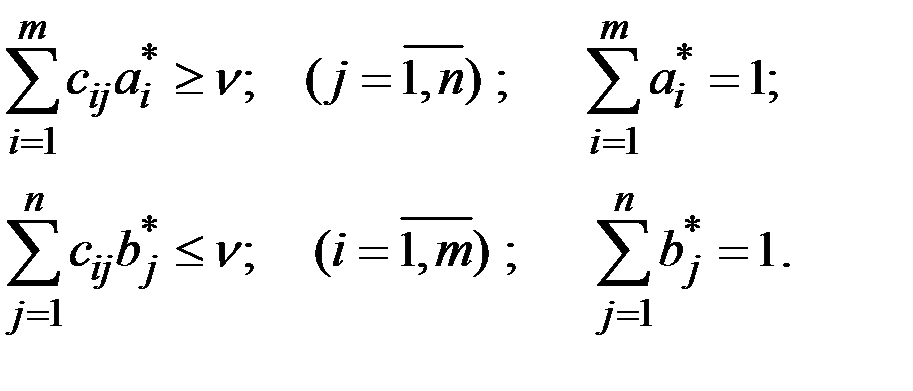
Чтобы выполнялось условие n > 0, прибавим ко всем элементам матрицы С число K =10, что не изменит оптимальных стратегий, а лишь увеличит цену игры на K =10, и сделаем замены переменных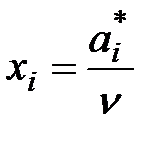 
.
1. Имеем задачу линейного программирования для стратегий первого игрока: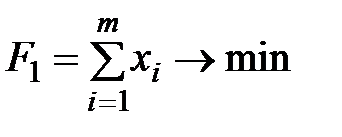 
при стратегиях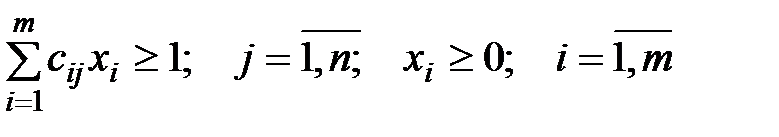 
.
2. Для второго игрока, сделав замену переменных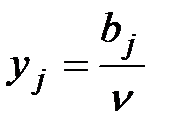 
получаем задачу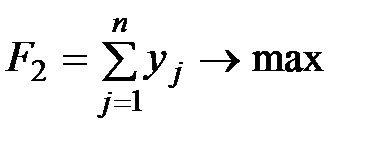 
при условиях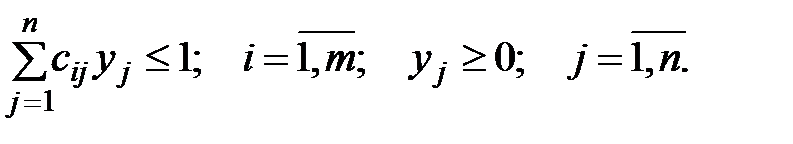 
Оптимальные стратегии игроков определяются соотношениями:
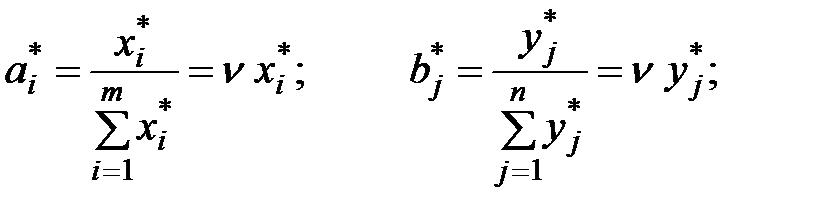
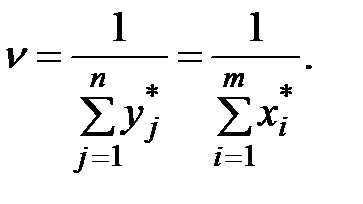
В нашем случае имеем задачи линейного программирования, симметричные для обоих игроков. Оптимальные стратегии игроков совпадут.
Для первого игрока имеем следующую модель:
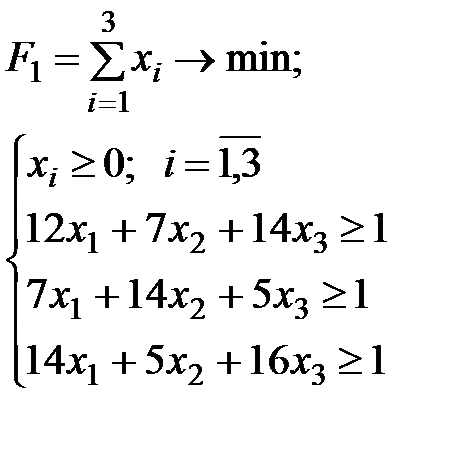
Решение этой задачи:
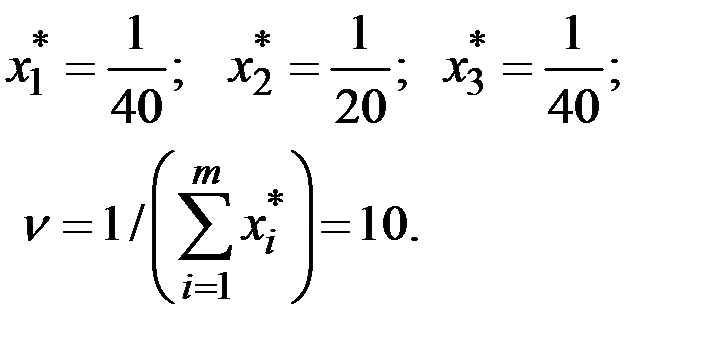
Тогда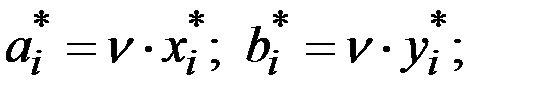 
, 
.
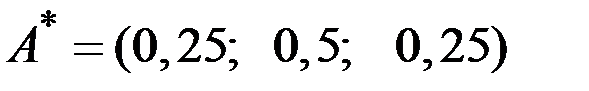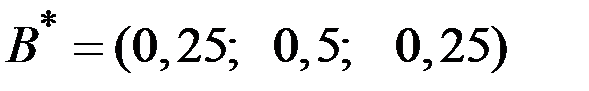При этих стратегиях исходная цена игры равна нулю.
Пример 8.7. Решить задачу для платёжной матрицы С =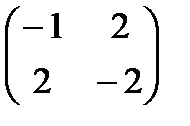 
Решение. Видим, что матрица симметричная, следовательно, оптимальные стратегии двух игроков совпадают. Определим стратегию первого игрока, составив модель проигрыша второго:
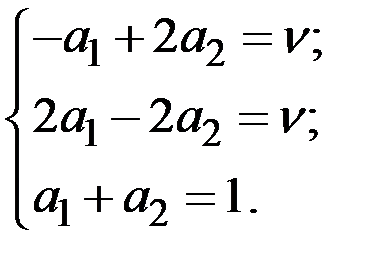
Сделаем эамену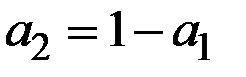 
. Получаем систему неравенств
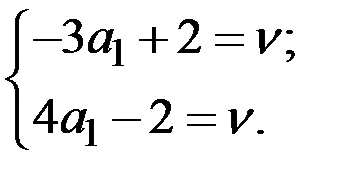
Построим прямые в интервале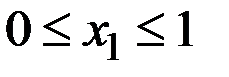 
:
Найдем координату цены игры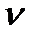 
, решив уравнение:
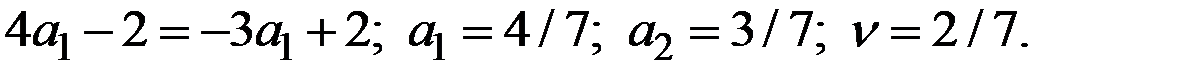
Оптимальная стратегия первого игрока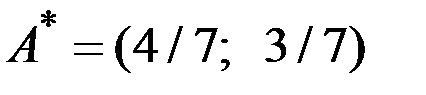 
.
Оптимальная стратегия второго игрока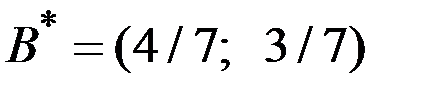 
.
Пример 8.8. Решить задачу итеративным методом для платёжной матрицы С =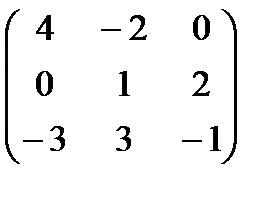 
.
Решение. Предположим начинает игрок А. Из трёх стратегий он выберет вторую, как предпочтительную. Игрок В ответит своей первой стратегией, как предпочтительной с наименьшим проигрышем и т.д.
Запишем итерации в таблицу:
| n | i | SB1 | SB2 | SB3 | MinS(n) | j | SA1 | SA2 | SA3 | MaxS(n) | S(n) |
| 1 | 2 | 0 | 1 | 2 | 0 | 1 | 4 | 0 | –3 | 4 | 2 |
| 2 | 1 | 4 | –1 | 2 | –1/2 | 2 | 2 | 1 | 0 | 1 | 1/4 |
| 3 | 3 | 1 | 2 | 1 | 1/3 | 1 | 6 | 1 | –3 | 2 | 7/6 |
| 4 | 1 | 5 | 0 | 1 | 0 | 2 | 4 | 2 | 0 | 1 | 1/2 |
| 5 | 3 | 2 | 3 | 0 | 0 | 1 | 8 | 2 | –3 | 8/5 | 4/5 |
| 6 | 1 | 6 | 1 | 0 | 0 | 2 | 6 | 3 | 0 | 1 | 1/2 |
| 7 | 3 | 3 | 4 | –1 | –1/7 | 1 | 10 | 3 | –3 | 10/7 | 9/14 |
| 8 | 1 | 7 | 2 | –1 | –1/8 | 2 | 8 | 4 | 0 | 1 | 9/16 |
| 9 | 3 | 4 | 5 | –2 | –2/9 | 1 | 12 | 4 | –3 | 4/3 | 5/9 |
| 10 | 1 | 8 | 3 | –2 | –1/5 | 2 | 10 | 5 | 0 | 1 | 2/5 |
Приняты следующие обозначения столбцов:
n – номер шага (итерации);
i – номер стратегии, выбранной игроком А;
j – номер стратегии, выбранной игроком В;
S В1 – «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В1 игрока В;
S В2 – «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В2 игрока В;
S В3 – «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В3 игрока В;
MinS(n) – минимальный средний выигрыш игрока А за n шагов;
S А1, S А2, S А3 – «накопленные» суммарные выигрыши игрока А за первые n шагов, соответственно, при стратегиях А1, А2, А3;
MaxS(n) – максимальный средний выигрыш игрока А;
S(n) – среднее арифметическое минимального среднего выигрыша и максимального среднего выигрыша игрока А.
Видим, что на 10–м шаге приближённая цена игры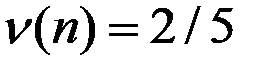 
.
Смешанные стратегии определяются частотами появления чистых стратегий: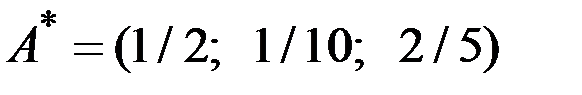 
,
.
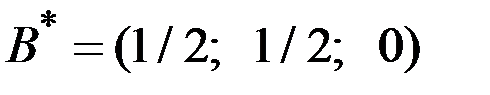Пример 8.9. Игрок А загадывает монету достоинством либо в 10 коп., либо в 50 коп. Если В отгадывает номинал монеты, то и получает её. В противном случае В платит игроку А 20 коп. Определить оптимальный способ ведения игры каждым игроком.
Решение. Имеем платёжную таблицу (матрицу):
| Стратегии | В10 | В50 |
| А10 | –10 | 20 |
| А50 | 20 | –50 |
Для нахождения оптимальной стратегии игрока А решим систему трёх уравнений:
→ 
→ 
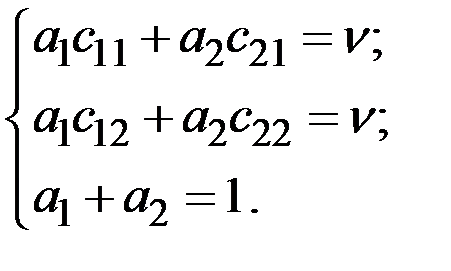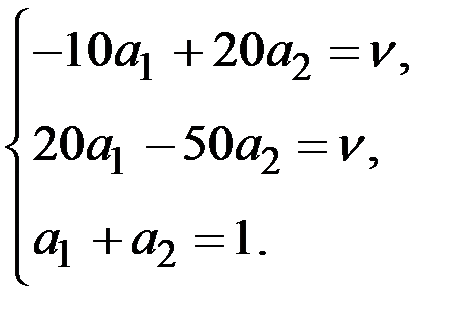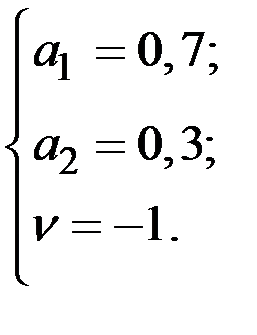
Для второго игрока оптимальная стратегия будет симметричной
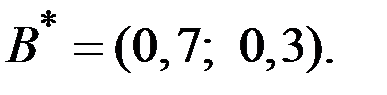
Дата: 2019-03-05, просмотров: 386.
