Пример 8.3. Фирма планирует начать выпуск двух моделей обуви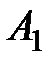 
и 
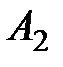. Спрос на модели не определён, но можно предположить, что он может принимать одно из двух состояний 
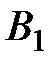или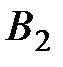 
. В зависимости от этих состояний прибыль фирмы различна и определяется матрицей
C=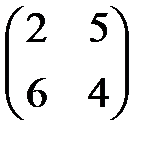 
.
Найти соотношение между объёмами выпуска каждой из моделей, при котором фирме гарантируется максимально возможная средняя прибыль при любом состоянии спроса.
Решение. Прежде всего проверим наличие седловой точки в данной матрице. Для этого найдём минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5).
Нижняя цена игры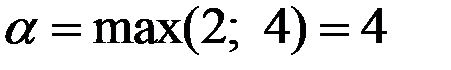 
,
а верхняя цена игры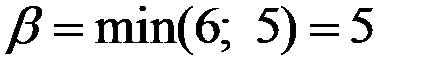 
.
Так как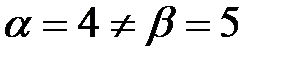 
, то решением игры являются смешанные оптимальные стратегии, а цена игры 
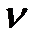заключена в пределах 
.
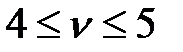1. Пусть для игрока А оптимальная стратегия задаётся вектором
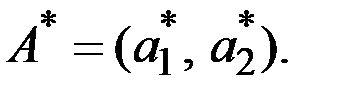
Тогда при применении игроком В чистой стратеги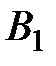и 
или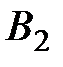 
игрок А получит средний выигрыш, равный цене игры, т.е.
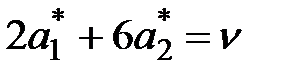(при стратегии );
(при стратегии ).
Помимо двух записанных уравнений относительно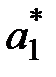 
и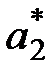 
добавим уравнение, связывающее эти частоты 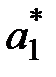и :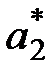 
.
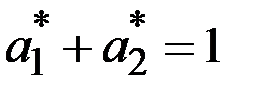Решая полученную систему трёх уравнений с тремя неизвестными, находим: 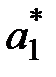= 0,4; 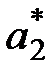= 0,6;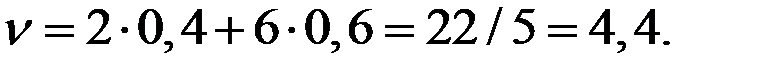 
2. Найдём теперь оптимальную стратегию для игрока В.
Пусть оптимальная стратегия для второго игрока задаётся вектором
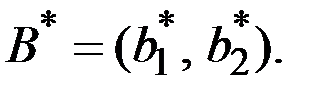
Тогда имеем систему уравнений (по строкам)
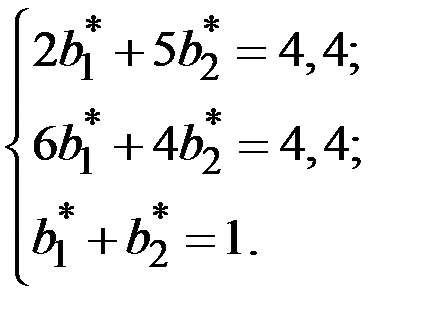
Решая эту систему уравнений, состоящую из каких–нибудь двух уравнений, взятых из последней системы, получим
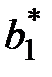= 0,2; 
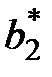= 0,8.
Следовательно, решением игры являются смешанные стратеги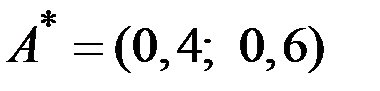и
и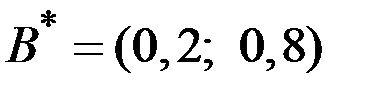 
,
а цена игры
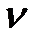= 4,4.
Дадим геометрическую интерпретацию решения данной игры.
Для этого на плоскости введём систему координат и на оси абсцисс отложим отрезок единичной длины 
, каждой точке которого поставим в соответствие некоторую смешанную стратегию первого игрока (рис. 8.1) с частотой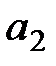 
.
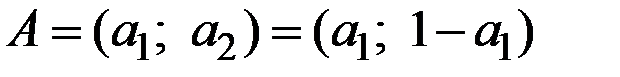В частности, точке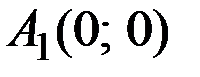 
отвечает стратегия A1 и т.д.
В точках A1 и A2 восставим перпендикуляры и на полученных прямых будем откладывать выигрыш игрока А.
На первом перпендикуляре (в данном случае он совпадает с осью ординат) отложим выигрыш игрока А при стратегии A1, а на втором – при стратегии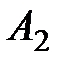 
.
Если игрок A применяет стратегию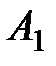 
, то его выигрыш при стратегии 
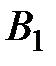игрока В равен 2, а при стратегии 
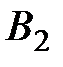он равен 5.
Числам 2 и 5 на оси ординат соответствуют точк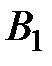и 
и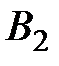 
.
Если же игрок А применяет стратегию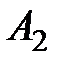 
, то его выигрыш при стратегии 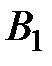игрока В равен 6, а при стратегии 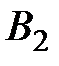он равен 4.
Эти два числа определяют две точк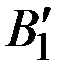и 
и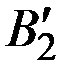 
на перпендикуляре, восстановленном в точке .
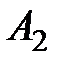Соединяя между собой точк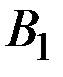и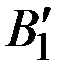 
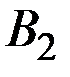и , 
и 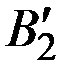, получим две прямые, расстояние до которых от оси абсцисс определяет средний выигрыш первого игрока при любом сочетании соответствующих стратегий.
Например, расстояние от любой точки отрезка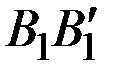 
до оси абсцисс определяет средний выигрыш 
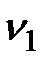при конкретном cочетании стратегий A1 и 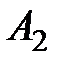(с частотам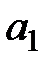и 
и 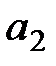) и стратегии 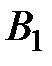игрока B.
Это расстояние равно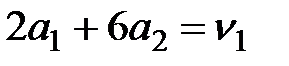 
.
Аналогично, средний выигрыш при применении стратегии 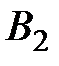определяется ординатами точек, принадлежащих отрезку 
.
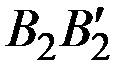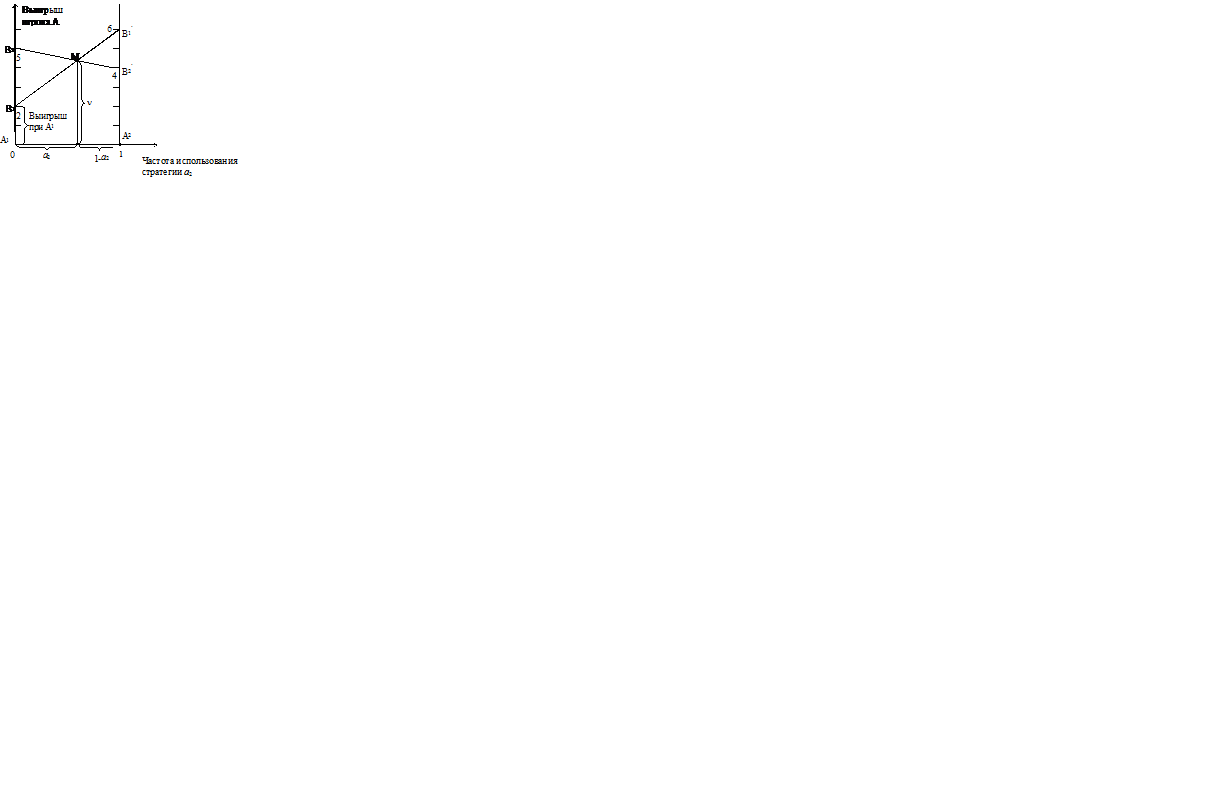
Рис. 8.1. Графическое решение задачи 8.3
Таким образом, ординаты точек, принадлежащих ломаной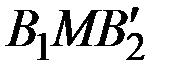 
, определяют минимальный гарантированный выигрыш игрока А при применении им любых смешанных стратегий.
Эта минимальная величина является максимальной в точке M; следовательно, этой точке соответствует оптимальная стратегия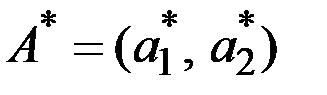 
, а её ордината равна цене игры .
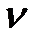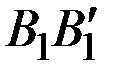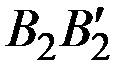Координаты точки М находим как координаты точки пересечения прямых и . Соответствующие три уравнения имеют вид
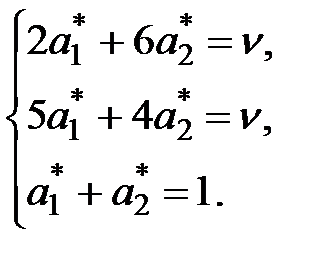
Решая эту систему уравнений, получаем
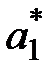= 2/5; 
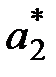= 3/5; 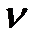= 22/5 = 4,4.
Аналогично находится оптимальная стратегия для игрока B.
Для её определения имеем уравнения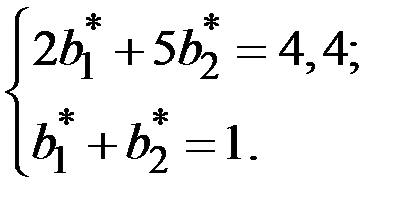 
Решение этой системы: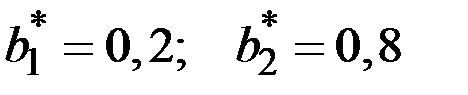 
.
Следовательно, решением игры являются смешанные стратеги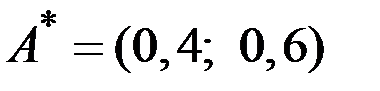и
и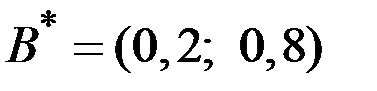 
,
а цена игры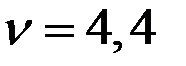 
.
Пример 8.4. Найти решение игры, заданной матрицей
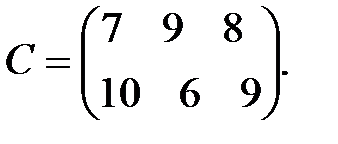
Решение. На рис. 8.2 прямые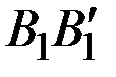 
, 
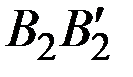и 
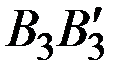соответствуют стратегиям игрока В , а ломаная 
– нижней границе выигрыша игрока А.
Игра имеет решение
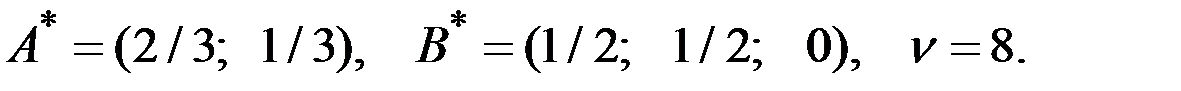
Рис. 8.2. Графическое решение задачи 8.4
Дата: 2019-03-05, просмотров: 228.
