Пусть имеется два игрока, один из которых может выбрать i–ю стратегию из т своих возможных стратегий ( 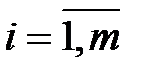 ), а второй, не зная выбора первого, выбирает j–ю стратегию из n своих возможных стратегий (
), а второй, не зная выбора первого, выбирает j–ю стратегию из n своих возможных стратегий ( 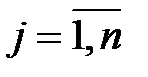 ).
).
В результате первый игрок выигрывает величину 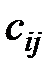 , а второй проигрывает эту величину.
, а второй проигрывает эту величину.
Из чисел 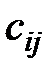 составим матрицу
составим матрицу
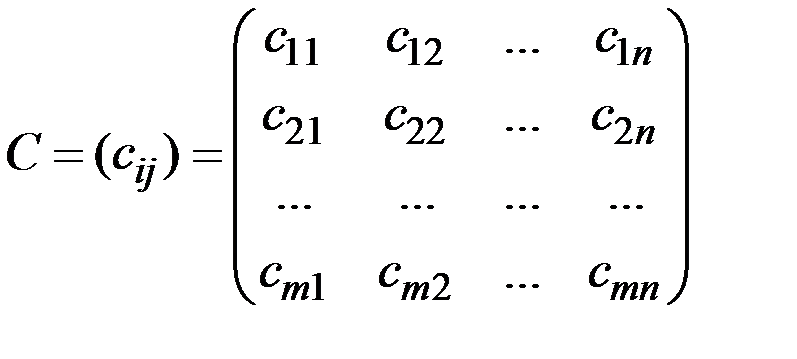 .
.
Строки матрицы C соответствуют стратегиям первого игрока, а столбцы – стратегиям второго. Эти стратегии называются чистыми.
Матрица C называется платёжной матрицей игры.
Игру, определяемую матрицей C, имеющей m строк и n столбцов, называют конечной игрой размерности 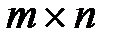 .
.
Тройка понятий <A, B, C> называется антогонистической игрой,
где А и В – множества стратегий первого и второго игроков;
С – функция от переменных а О А и b О B (платёжная матрица).
Число 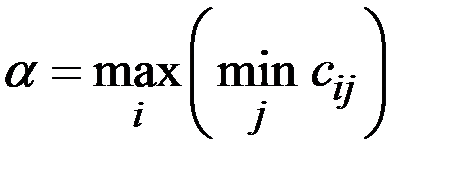 называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) – максиминной.
называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) – максиминной.
Число 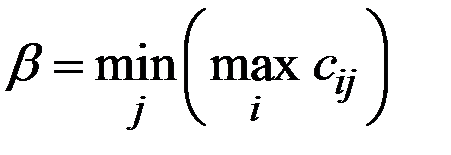 называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) – минимаксной.
называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) – минимаксной.
Нижняя цена игры всегда не превосходит верхнюю цену игры b і a.
Если 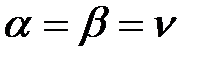 , то число
, то число 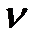 называется ценой игры.
называется ценой игры.
Игра, для которой 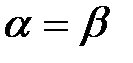 , называется игрой с седловой точкой.
, называется игрой с седловой точкой.
Для игры с седловой точкой решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными.
Пример 8.1. Швейное предприятие планирует к массовому выпуску три новые модели одежды. Спрос на эти модели не может быть точно определён. Однако можно предположить, что величина спроса характеризуется четырьмя возможными состояниями.
С учётом этих состояний анализируются три возможных варианта (по объёму) выпуска моделей (А1, А2, А3). Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счёте различный эффект.
Прибыль (млн. руб.), которую получает предприятие при различных вариантах выпуска моделей и соответствующем состоянии спроса, определяется матрицей
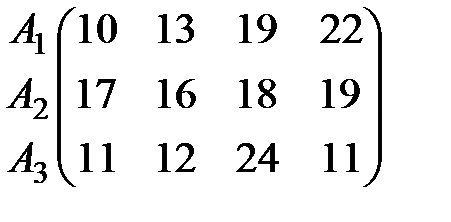 .
.
Требуется найти вариант выпуска моделей одежды, обеспечивающий максимальную среднюю величину прибыли при любом состоянии спроса.
Решение. Проверим, имеет ли исходная матрица седловую точку.
Для этого находим минимальные элементы в её строках (10; 16; 11) и максимальные – в столбцах (17; 16; 24, 22).
Максимальным среди минимальных элементов строк является число 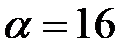 , а минимальным среди максимальных элементов столбцов – число
, а минимальным среди максимальных элементов столбцов – число 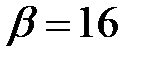 . Таким образом,
. Таким образом, 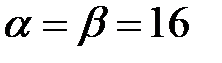 . Число 16 является ценой игры.
. Число 16 является ценой игры.
Игра имеет седловую точку, соответствующую второму варианту выпуска модели одежды.
Объём выпуска модели, соответствующей данному варианту, обеспечивает прибыль в 16 млн. руб. при любом состоянии спроса.
Если игра, заданная платёжной матрицей, не имеет седловой точки, то для нахождения её решения используются смешанные стратегии.
Вектор, каждая из компонент которого показывает относительную частоту (вероятность) использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.
Сумма компонент указанного вектора равна единице, а сами компоненты (частоты) не отрицательны.
Смешанную стратегию первого игрока обозначим как вектор
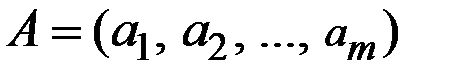 ,
,
а второго игрока – как вектор
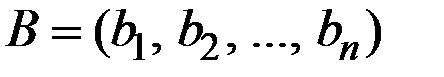 ,
,
где ai и bj – вероятности соответствующих чистых стратегий
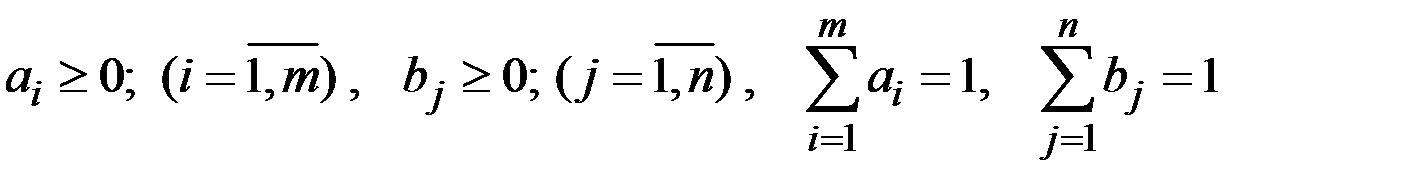 .
.
Функцией выигрыша (платёжной функцией) с матрицей С называется средняя величина выигрыша первого игрока:
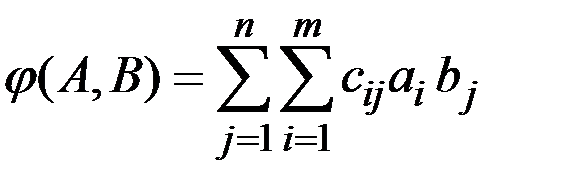
Стратегии A* и B* называются оптимальными для игроков, если выполняется соотношение
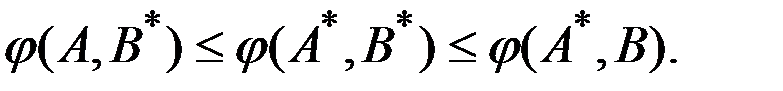
Если A*– оптимальная стратегия первого игрока, а B* – оптимальная стратегия второго игрока, то ценой игры является игры число
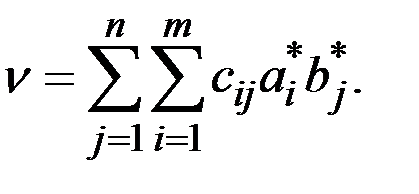
Определение оптимальных стратегий и цены игры и составляет процесс нахождения решения игры.
Теорема Неймана утверждает, что всякая конечная матричная игра с нулевой суммой имеет решение в смешанных стратегиях.
Для того чтобы число 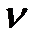 было ценой игры, а A* и B* – оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
было ценой игры, а A* и B* – оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
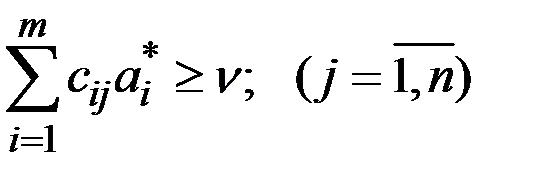 :
:
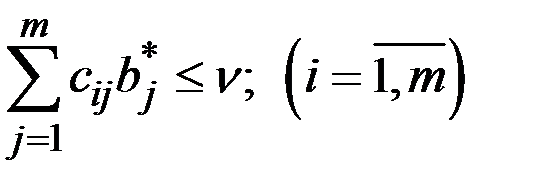 .
.
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен (не менее) цене игры 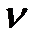 вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).
вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).
Пара оптимальных стратегий A* и B*, образующих решение игры, обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей.
Пример 8.2. Найти нижнюю цену игры, верхнюю цену игры, седловую точку, оптимальные чистые стратегии и цену игры (если они существуют) для платёжной матрицы С = 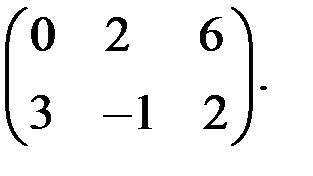
Решение. Нижнюю и верхнюю цену игры найдём по определению
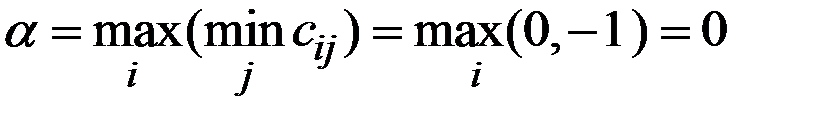 ;
;
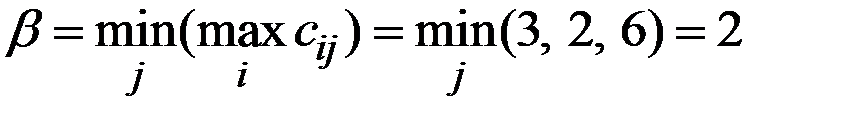 .
.
Так как 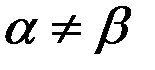 , то седловых точек нет и решение следует искать в смешанных стратегиях.
, то седловых точек нет и решение следует искать в смешанных стратегиях.
Упростим матрицу. Заведомо невыгодных и дублирующих строк не найдено, заведомо невыгодный третий столбец (по отношению ко второму столбцу) убираем (присваивая нулевую вероятность).
Перепишем получившуюся матрицу: С = 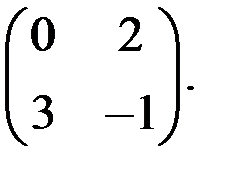
Решим игру 2×2 стандартным методом из системы уравнений.
Для нахождения оптимальной стратегии игрока А решим систему:
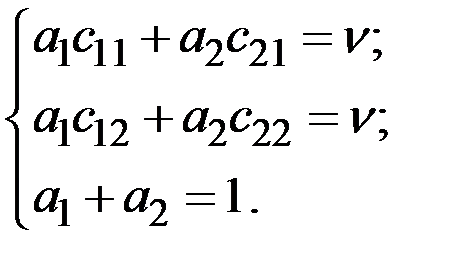 →
→ 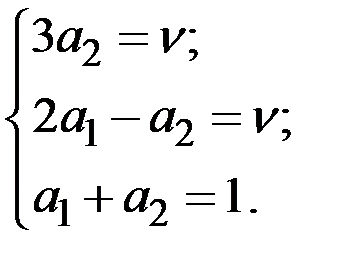 →
→ 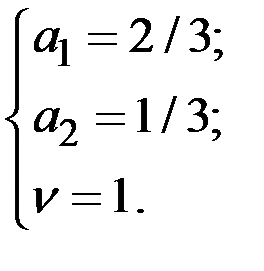
Для нахождения оптимальной стратегии игрока В решим систему:
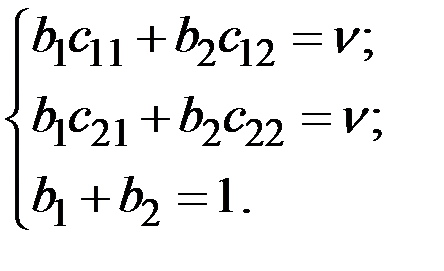 →
→ 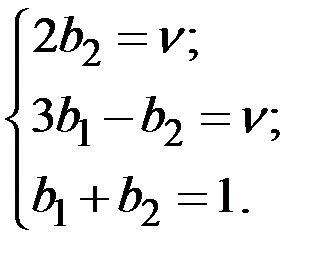 →
→ 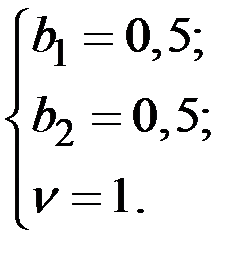
Цена игры 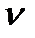 = 1.
= 1.
Оптимальная стратегия первого игрока 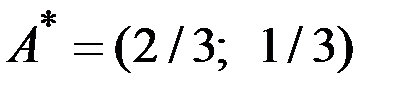 .
.
Оптимальная стратегия второго игрока 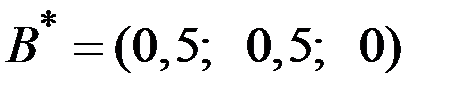 .
.
Дата: 2019-03-05, просмотров: 448.