Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Регрессионный анализ

Все переменные любой модели в зависимости от конечных прикладных целей её использования принято делить на экзогенные, эндогенные и предопределённые.

Экзогенные – это переменные, которые входят в модель, но рассматриваются как определённые независимо от моделируемого явления.

Экзогенные переменные заданы как бы «извне», автономно.

В определённой степени это управляемые (планируемые) независимые (объясняющие) переменные.

Эндогенные – это выходные (результирующие) переменные, которые определяются только явлением, для которого строится модель.

Значения этих переменных формируются в процессе и внутри функционирования анализируемой системы (в существенной мере под воздействием экзогенных переменных и во взаимодействии друг с другом).

В модели они являются предметом объяснения, и в этом смысле их иногда называют зависимыми (объясняемыми) переменными.

Предопределённые – это переменные, выступающие в системе в роли факторов (аргументов) или объясняющих переменных.

Множество предопределённых переменных формируется из всех экзогенных переменных (которые могут быть «привязаны» к прошлым, текущему или будущим моментам времени) и так называемых лаговых эндогенных переменных, т.е. таких эндогенных переменных, значения которых входят в уравнения анализируемой системы измеренными в прошлые (по отношению к текущему) моменты времени, а следовательно, являются уже известными, заданными.

Модель и служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.

Между двумя переменными (показателями, величинами) может существовать функциональная связь, когда каждому значению величины Х соответствует определённое значение другой величины Y:

.

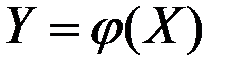Функциональные связи характеризуются полным соответствием между изменением факторных признаков и изменением результативной величины, то есть каждому конкретному набору значений факторов соответствует определённое значение результативного признака.

Например, при повремённой оплате труда размер зарплаты функционально зависит от количества отработанного времени.

Стохастическая связь состоит в том, что одна величина реагирует на изменение другой изменением своего закона распределения.

Частный случай стохастической связи – статистическая связь (корреляционная), когда условное математическое ожидание одной величины реагирует на изменение другой величины.

Регрессионный анализ и занимается построением и исследованием статистической связи между изучаемыми показателями.

Регрессионный анализ выполняется в 3 этапа.

1. Выбор формы связи между переменными, т.е. модели регрессии.

2. Оценка неизвестных параметров выбранной модели.

3. Оценка качества полученной модели и проверка соответствующих статистических гипотез о модели регрессии.

1. Форма связи между переменными, т.е. вид уравнения регрессии, выбирается исследователем либо из каких–то теоретических предпосылок, либо из соображений удобства работы с этой моделью, либо из вида и анализа графического изображения имеющихся статистических данных, либо из совокупности возможных математических моделей, выбрав подходящую с помощью соответствующего критерия приближения к имеющимся данным, либо из других каких–либо соображений (предпочтений).

2. Для оценки параметров модели наиболее часто используют метод наименьших квадратов (МНК). Основной принцип МНК заключается в том, чтобы так определить неизвестные параметры модели, чтобы сумма квадратов отклонений имеющихся данных от выбранной модели (уравнения) регрессии была бы минимальной:

.

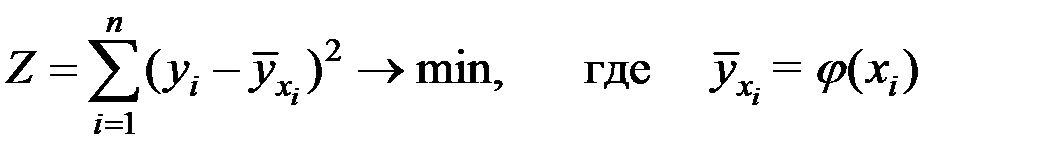МНК удобен тем, что производная от этого критерия часто даёт линейное уравнение относительно неизвестных параметров модели.

3. Для оценки качества регрессионных моделей целесообразно:

1) вычислить и оценить значимость соответствующего параметра корреляционного анализа (линейного коэффициента корреляции, коэффициента множественной корреляции, индекса корреляции и др.);

2) проверить адекватность (значимость) всей модели регрессии;

3) оценить точность модели, т.е. вычислить среднее квадратическое отклонение остатков ;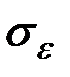

4) проверить значимость каждого параметра модели регрессии;

5) определить доверительные границы всей модели регрессии;

6) определить доверительные границы (интервальные оценки) каждого параметра модели регрессии.

 

Качество модели обычно оценивается по адекватности и точности на основе анализа остатков регрессии, т.е. разности наблюдаемых и расчётных значений зависимой переменной:

.

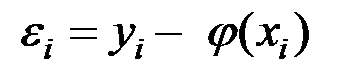Расчётные значения 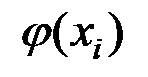 получаются путём подстановки в модель фактических значений всех включённых факторов. Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов.

Согласно общим предположениям регрессионного анализа остатки должны вести себя как независимые (почти независимые) одинаково распределённые случайные величины.

В классических методах регрессионного анализа предполагается также нормальный закон распределения остатков. Независимость остатков проверяется с помощью критерия Дарбина – Уотсона.

Для проверки значимости модели регрессии часто используется F–критерий Фишера с использованием коэффициента детерминации:

.

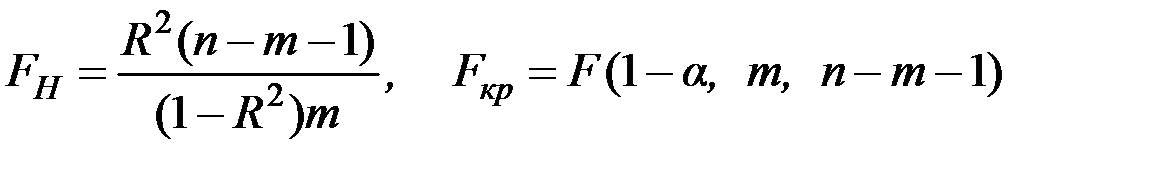Если расчётное значение 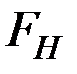  больше табличного (критического) значения  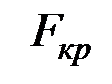 с v₁= m и v₂ = (п – m – 1) степенями свободы (где m – количество независимых факторов, включённых в модель) при заданном уровне значимости 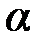, то модель считается значимой.

В качестве меры точности применяют несмещённую оценку среднего квадратического отклонения (стандартную ошибку оценки), т.е. корень из дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к числу степеней свободы, т.е. к величине (п – m – 1), (где m – количество факторов, включённых в модель):

.

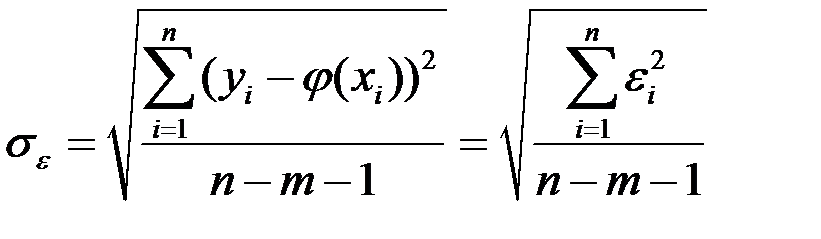где                                            

.

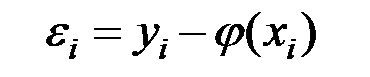Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.

Прогнозируемое значение переменной у_пр получается при подстановке в уравнение регрессии ожидаемой величины фактора х_пр.

Данный прогноз называется точечным.

При выборе ожидаемой величины х_пр нельзя подставлять значения независимой переменной х_пр, значительно отличающиеся от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.

Вероятность реализации точечного прогноза практически равна нулю.

Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой вероятностью (надёжностью).

Доверительный интервал линии регрессии (рис. 5.1) определяется соотношением:

.

 

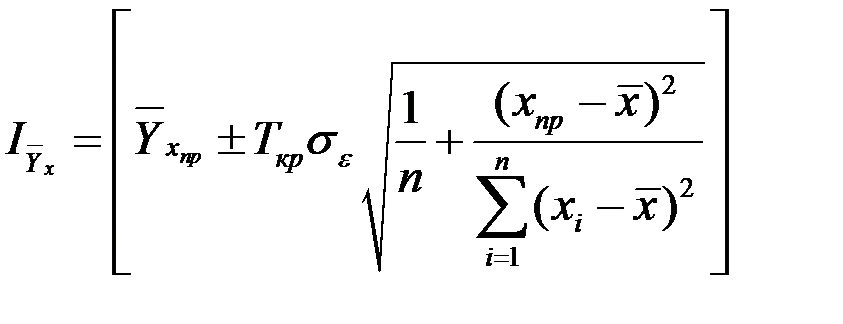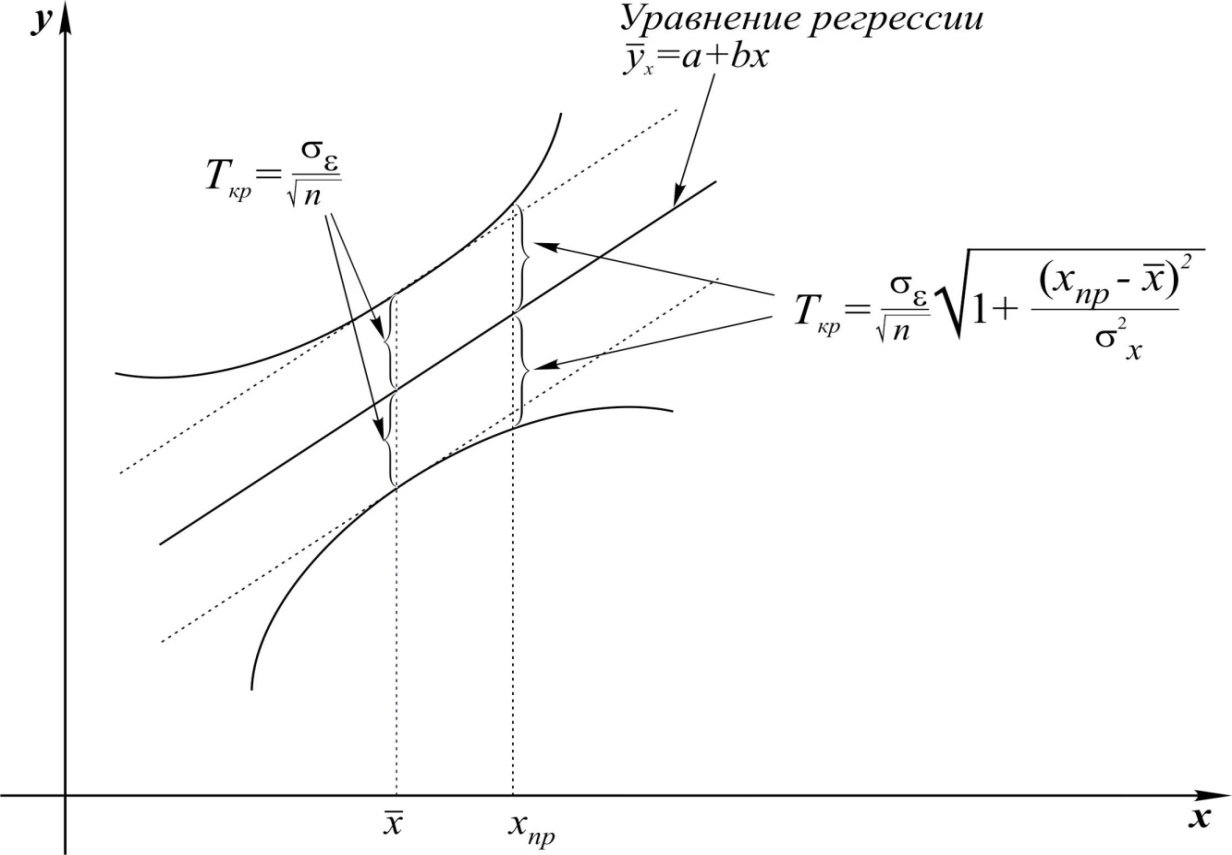
Рис. 5.1. Доверительные границы для уравнения регрессии

 

Стандартная ошибка линии регрессии определяется соотношением

.

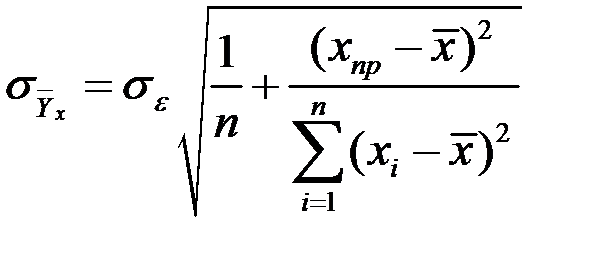Доверительный интервал для прогнозов индивидуальных значений 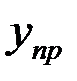 определяется из соотношения:

,

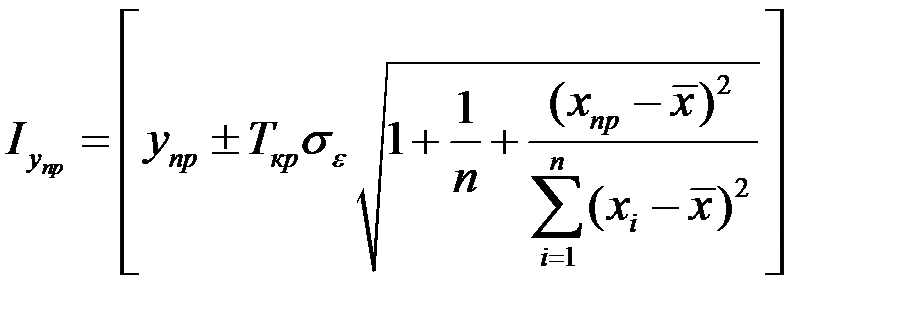где 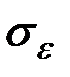 – стандартная ошибка зависимой переменной;

х = х_пр – значение фактора X, используемое для прогноза;

п – число наблюдений.

Линейная парная регрессия

Здесь имеется в виду, что переменная Y предположительно находится под влиянием переменной X в линейной зависимости:

.

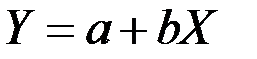Для отдельного наблюдения имеем соотношение:

,

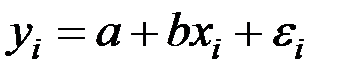где a – постоянная величина (свободный член уравнения);

b – коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений;

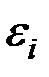 – остатки (ошибки) модели.

Коэффициент регрессии характеризует изменение переменной Y при изменении значения Х на единицу. Если b > 0 – переменные Х и Y положительно коррелированные, если b < 0 – отрицательно коррелированные.

Остатки 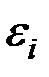 предполагаются независимыми, нормально распределёнными величинами с нулевым математическим ожиданием и постоянной дисперсией.

Для оценки параметров модели МНК даёт следующее решение

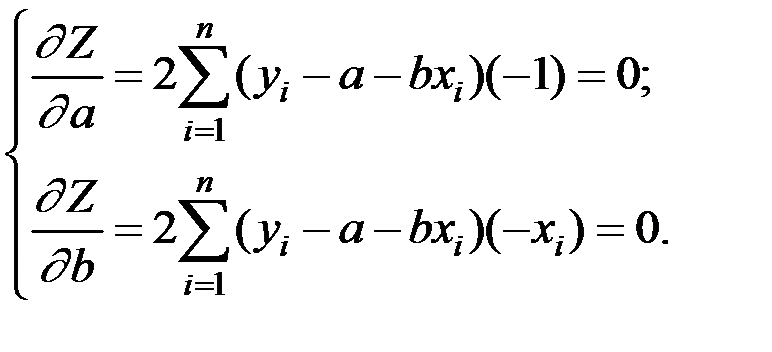
Для нахождения параметров а и b необходимо решить систему двух линейных уравнений с двумя неизвестными (полученных из МНК)

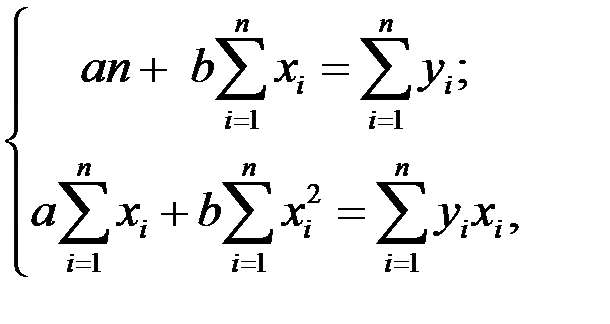
где 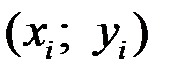 – фактические значения переменных; n – число наблюдений.

В результате получаем искомые параметры:

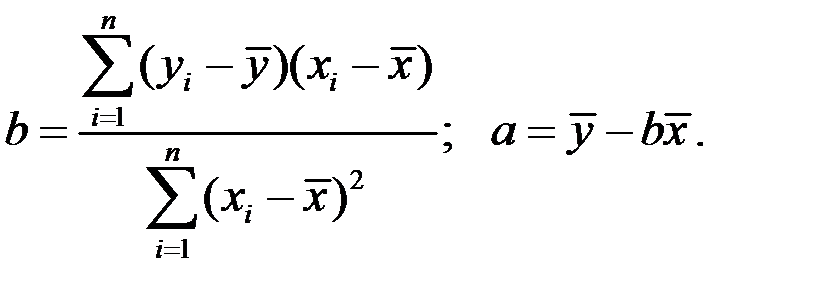
Такое решение может существовать только при выполнении условия

.

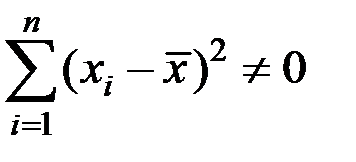Это условие называется условием идентифицируемо сти модели наблюдений 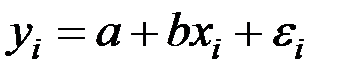 и означает, что не все значения x₁, ..., x_n совпадают между собой. Это равносильно отличию от нуля определителя коэффициентов системы нормальных уравнений.

При нарушении этого условия все точки (x_i, y_i), i = 1, ... , п, лежат на одной вертикальной прямой .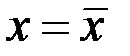

Выражение для b можно записать и в другом виде

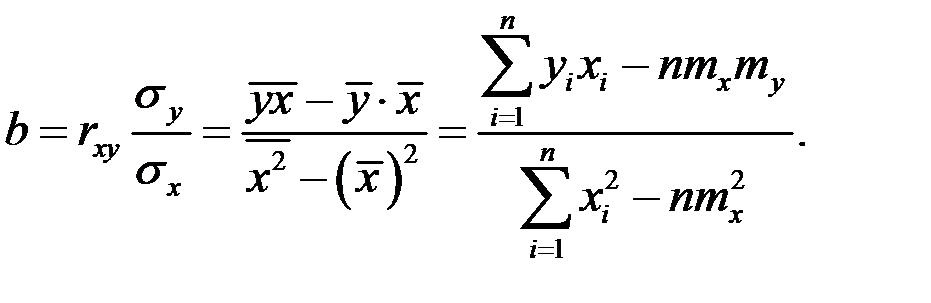
В случае системы двух нормальных СВ и линейной связи между ними Y = a + bX с использованием вычисленных оценок основных числовых характеристик переменных по выборке МНК даёт следующее решение

,

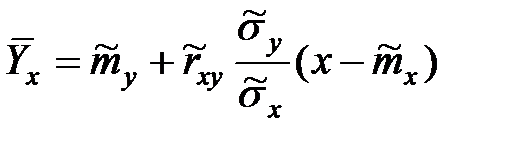где  

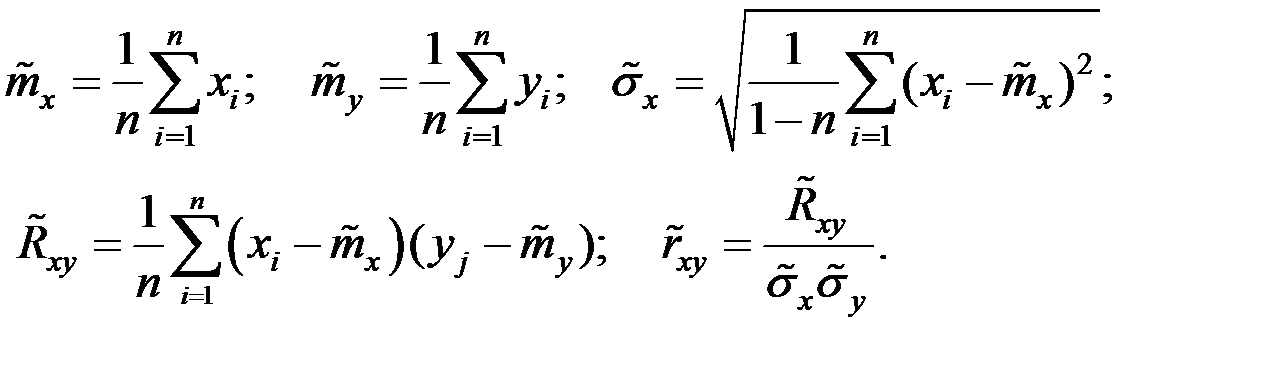
Аналогично,

.

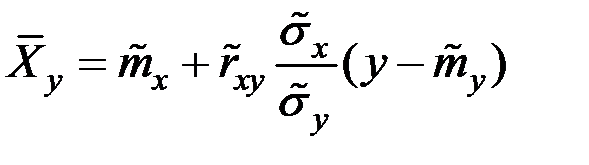Нелинейная парная регрессия

Если между явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают 2 класса моделей нелинейных регрессий:

1) регрессии, нелинейные относительно переменных, но линейные по параметрам (полиномы разных степеней, гипербола и др.);

2) регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная и др.).

Регрессии, нелинейные относительно переменных, определяются (как и линейные) на основе МНК. Так в случае поиска уравнения регрессии в виде полинома k–й степени, исходя из основного принципа МНК

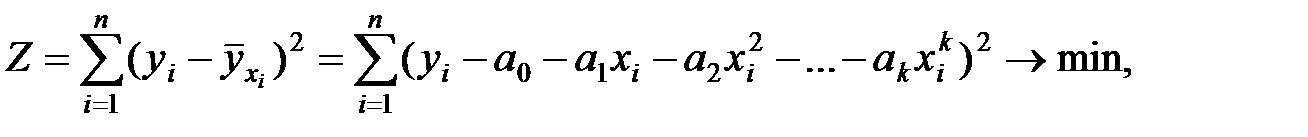
вычисляя и приравнивая частные производные критерия Z по каждому неизвестному параметру к нулю ( 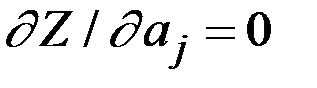), получим систему уравнений

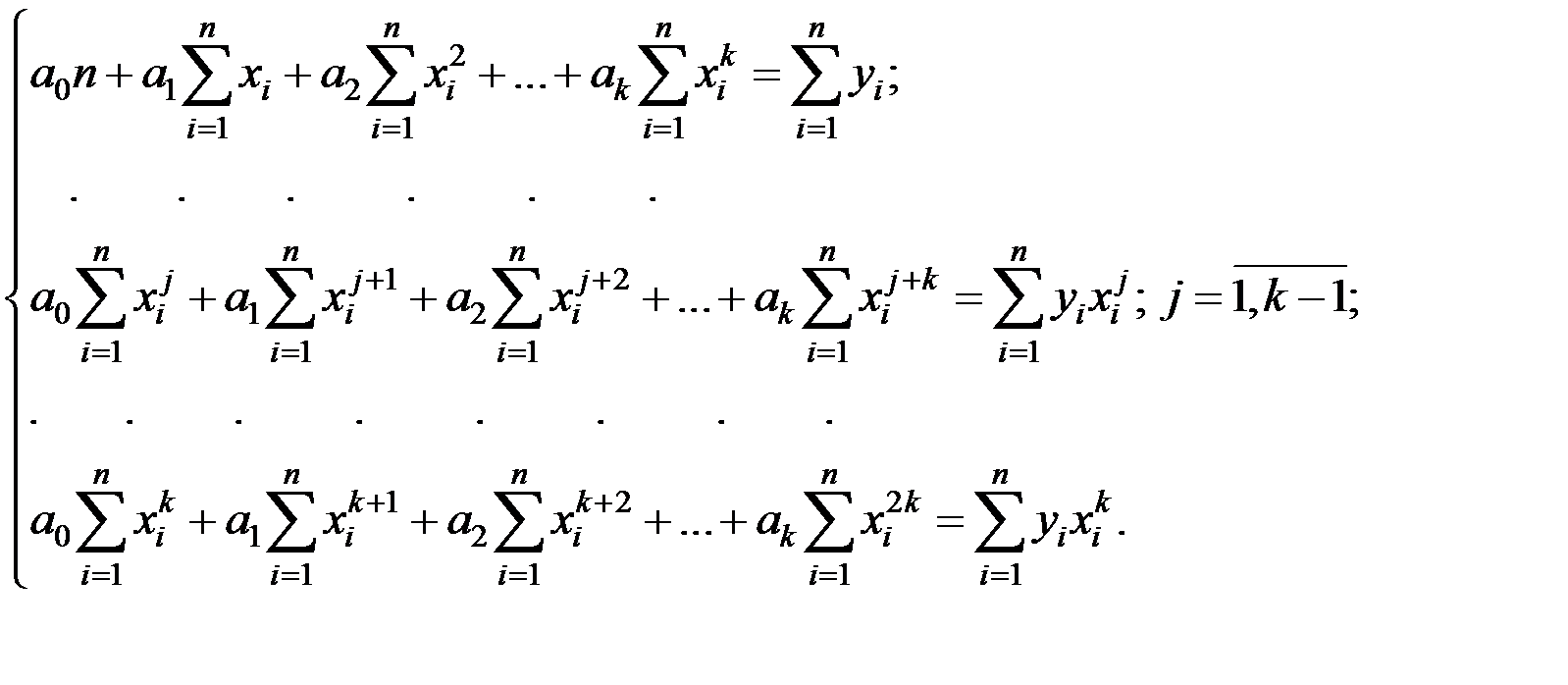
Решая эту систему, найдём неизвестные параметры .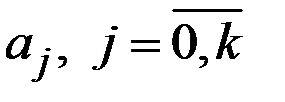

Регрессии, нелинейные по оцениваемым параметрам, подразделяются на:

1) нелинейные модели внутренне линейные;

2) нелинейные модели внутренне нелинейные.

Если модель нелинейна относительно параметров регрессии, то она в ряде случаев с помощью соответствующих преобразований может быть приведена к линейному виду.

Если же модель внутренне нелинейная, то она не может быть приведена к линейному виду. Для оценки параметров в этом случае используются итеративные (итерационные) процедуры, успешность которых зависит от вида уравнения и особенностей применяемого метода.

Множественная регрессия

B множественном регрессионном анализе пытаются найти зависимость одной зависимой переменной от нескольких независимых.

Связь между переменной 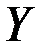 и m независимыми факторами можно охарактеризовать функцией регрессии

,

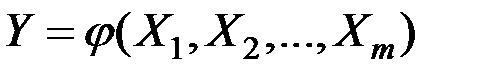которая показывает, каково будет в среднем значение переменной 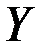, если переменные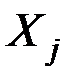 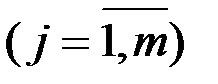  примут конкретные значения.

Основное значение имеют линейные модели (относительно параметров регрессии) в силу своей простоты. Нелинейные формы зависимости часто преобразуются к линейным путём линеаризации.

Наиболее приемлемым способом определения вида уравнения регрессии является метод перебора различных уравнений регрессии.

Наилучшие значения параметров регрессии 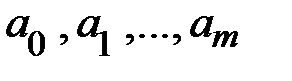 определяются МНК. Коэффициенты регрессии находятся по критерию:

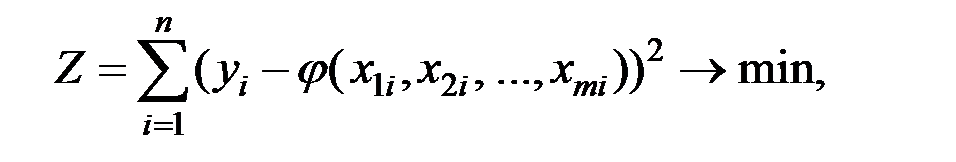
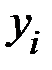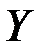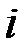где  – значение результативного фактора (зависимой переменной)  в –ом наблюдении;  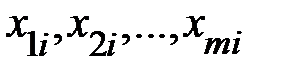– значения факторо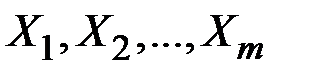в  в 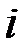–ом наблюдении;  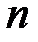– количество наблюдений.

Реализация этого критерия приводит к системе уравнений

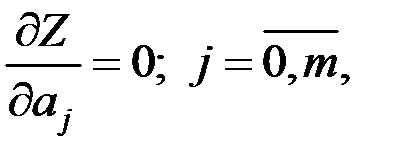
из которой определяются параметры .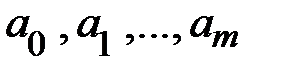

Линейная модель множественной регрессии имеет вид:

.

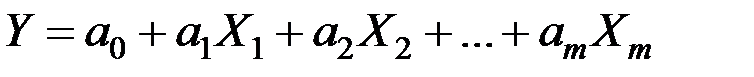Для имеющихся исходных данных 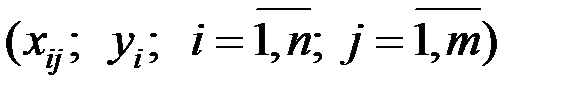 справедливо соотношение

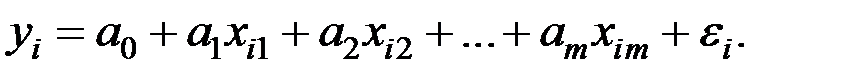
Введём в рассмотрение следующие матрицы:

.

 

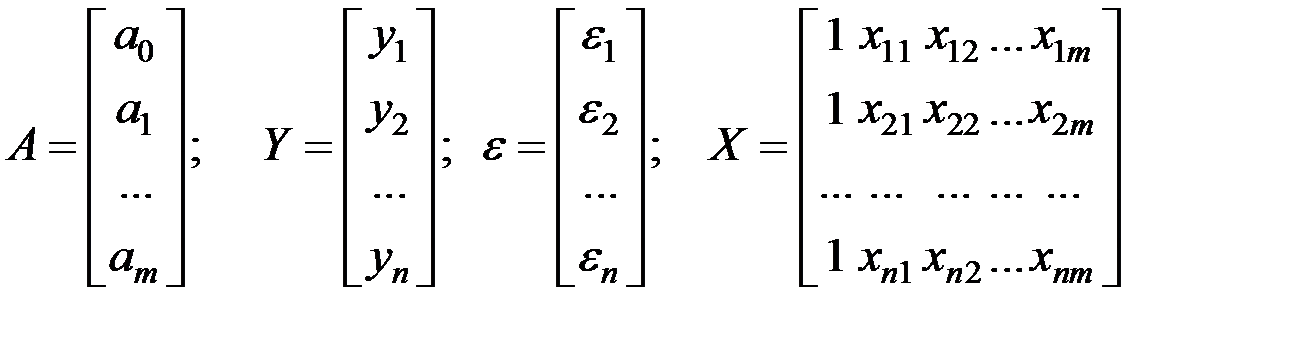Тогда модель регрессии имеет в матричном виде соотношение:

,

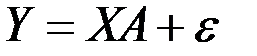где 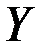 – вектор зависимой переменной размерности (п ´ 1), представляющий собой п наблюдений значений ;

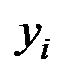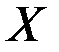 – матрица п наблюдений независимых переменных (X_l, X₂,  Х₃, ..., Х _m), размерность матрицы X равна п ´ (m + 1) (добавлен единичный столбец для определения а₀);

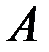 – подлежащий оцениванию вектор (матрица–столбец) неизвестных параметров размерности (m+1) ´ 1;

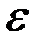 – вектор случайных отклонений (возмущений) размерности n ´ 1.

При применении МНК делаются определённые предпосылки (условия Маркова–Гаусса).

1. Математическое ожидание остатков равно нулю: .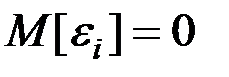

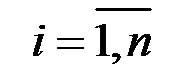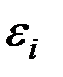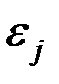2. Дисперсия остатков постоянна для любого   (условие гомоскедастичности), остатки  и  при 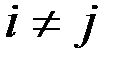 не коррелированы:

 

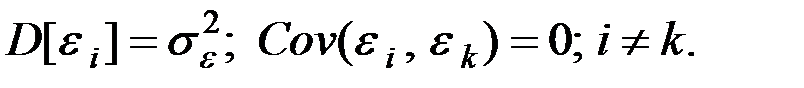
3. Ошибки 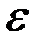 – нормально распределённый случайный вектор

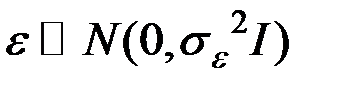(здесь  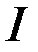– единичная матрица).

4. Столбцы матрицы X должны быть линейно независимыми, ранг матрицы X – максимальный (m + 1), а число наблюдений п превосходит ранг матрицы.

Для имеющихся исходных данных 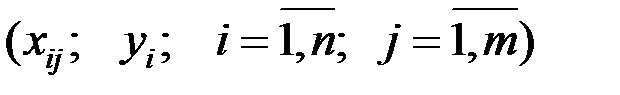 критерий МНК выглядит следующим образом:

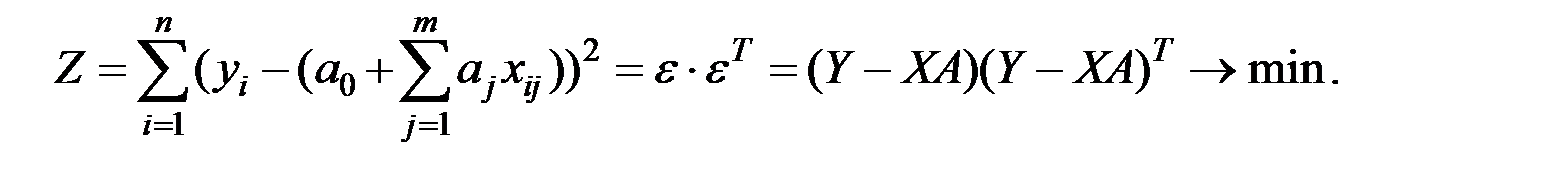
Здесь Т – символ транспонирования матрицы.

Для нахождения коэффициентов методом наименьших квадратов решаем систему линейных уравнений, которую получаем приравниванием частных производных к нулю:  

.

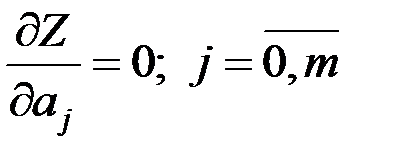В матричном виде решение множественного регрессионного анализа определяется соотношением:

.

 

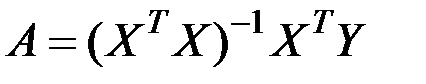Коэффициент регрессии 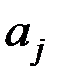 показывает, на какую величину в среднем изменится результативный признак 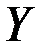, если переменную  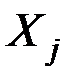увеличить на одну единицу своего измерения при неизменном значении других факторов, закреплённых на среднем уровне (т.е.  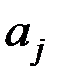является нормативным коэффициентом, имеет размерность отношения размерносте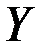й  и ).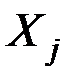

Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т.е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных линейно независимы.

Для экономических показателей это условие выполняется не всегда.

Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели.

В условиях мультиколлинеарности исходных показателей обычные оценки МНК имеют высокие значения стандартных ошибок (оценки неустойчивы). В этом случае часто используются другие методы оценки параметров регрессии.

Значимость отдельных коэффициентов регрессии проверяется по Т–критерию путём проверки гипотезы о равенстве нулю j–го параметра уравнения (кроме свободного члена):     

, ,

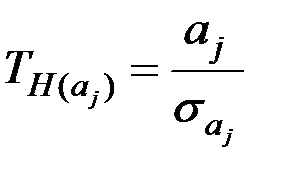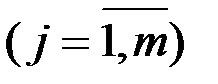где 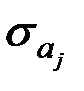 – стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии .

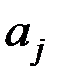Величина 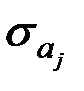 представляет собой квадратный корень из произведения несмещённой оценки точности модели  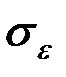и j–го диагонального элемента матрицы :           

.

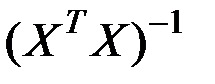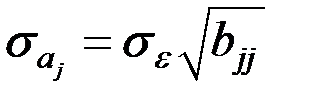Здесь 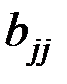 – диагональный элемент матрицы .

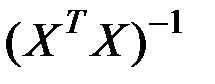В матричном виде имеем соотношение:

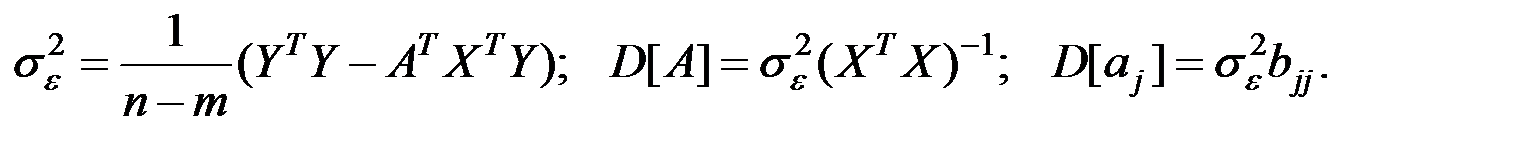
Табличное значение критерия 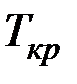 определяется при (n – 2) степенях свободы и соответствующем уровне значимости a (a = 0,1; 0,05; 0,01).

Если расчётное значение критерия 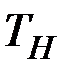 превосходит его табличное значение  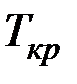при заданном уровне значимости, коэффициент регрессии считается значимым.

В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом её качество не ухудшится).

Доверительный интервал для коэффициентов регрессии имеет вид:

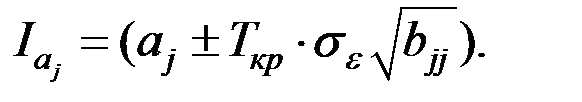
Значимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при независимых переменных:  

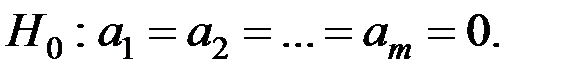
Для проверки значимости модели регрессии используется F–критерий Фишера, вычисляемый по формуле

,

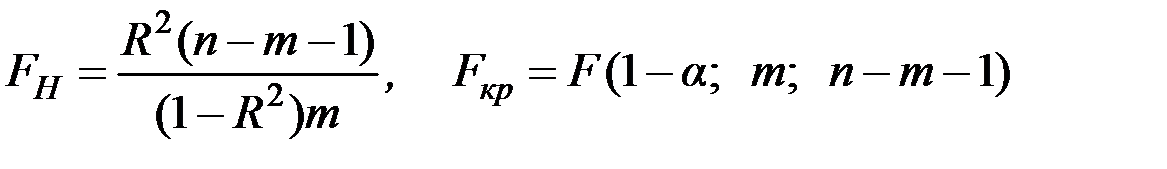где п – число наблюдений;

m – число независимых переменных, включённых в модель;

R² – коэффициент детерминации.

В целом качество модели оценивается по адекватности и точности на основе анализа остатков регрессии

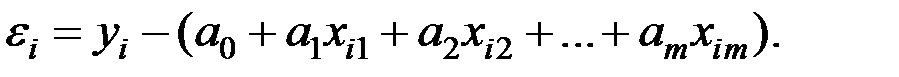
Расчётные значения результирующего показателя получаются путём подстановки в модель фактических значений всех включённых факторов.

Непосредственно с помощью коэффициентов регрессионной модели нельзя сопоставить факторы по степени их влияния на зависимую переменную из–за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации модели применяются коэффициенты эластичности 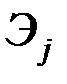 и бета–коэффициенты (стандартизованные коэффициенты регрессии) 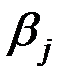, которые рассчитываются соответственно по формулам: 

         ,

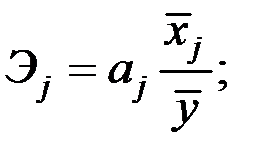
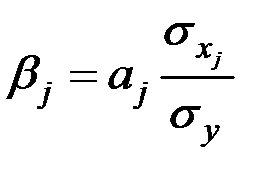где 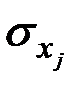 – среднеквадратическое отклонение фактора .

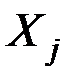Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент (не учитывает степень колеблемости факторов).

Бета–коэффициент показывает, на какую часть величины среднего квадратического отклонения 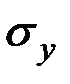 изменится зависимая переменная  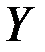изменением соответствующей независимой переменной  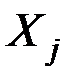на величину своего среднеквадратического отклонения  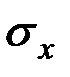при фиксированном на постоянном уровне значении остальных независимых переменных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

Уравнение регрессии в стандартизованной форме имеет вид:

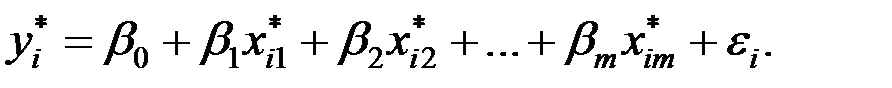
Здесь 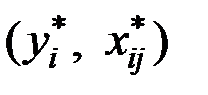 – стандартизованные переменные

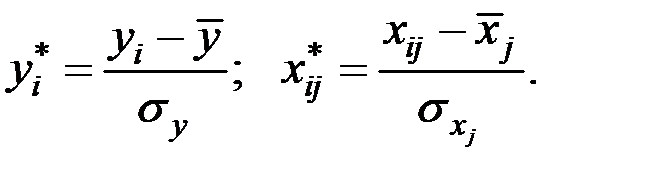
В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице.

Долю влияния каждого фактора в суммарном влиянии всех факторов можно оценить по величине дельта–коэффициентов:  

,

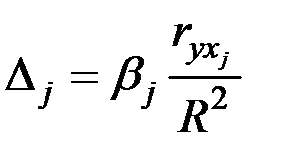где 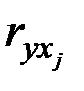– коэффициент парной корреляции между фактором  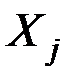и зависимой переменной 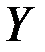;  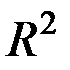– коэффициент детерминации.

При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных. Для прогнозирования зависимой переменной на τ шагов вперёд необходимо знать прогнозные значения всех входящих в неё факторов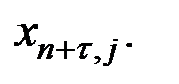  

Их оценки могут быть получены на основе экстраполяционных моделей или заданы пользователем (экспертно). Эти оценки подставляются в модель и получаются прогнозные оценки.

Для линейной модели множественной регрессии доверительный интервал рассчитывается следующим образом:

.

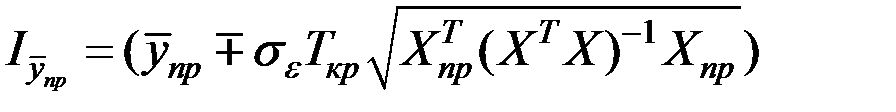Здесь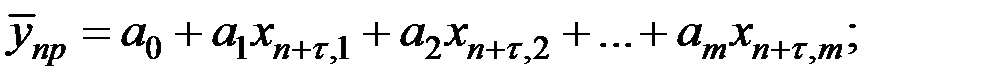 

.

 

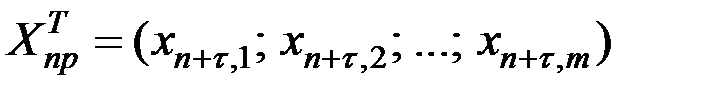Пример 5.1. По результатам изучения зависимости объёмов продаж компании в среднем за месяц от расходов на рекламу была получена следующая модель регрессии с распределённым лагом (млн. руб.):

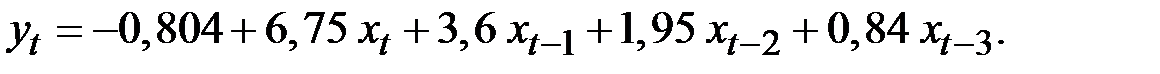
Проанализировать параметры этой модели.

Решение. В этой модели краткосрочный мультипликатор равен 6,75.

Это означает, что увеличение расходов на рекламу на 1 млн. руб. ведёт в среднем к росту объёма продаж компании на 6,75 млн. руб. в том же периоде.

Под влиянием увеличения расходов на рекламу объём продаж компании возрастёт в момент времени 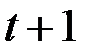 на 6,75 + 3,6 = 10,35 млн. руб., в момент  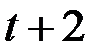возрастёт на 10,35 + 1,95 = 12,3 млн. руб.

Долгосрочный мультипликатор данной модели составит величину:

b = 6,75 + 3,6 + 1,95 + 0,84 = 13,14.

В долгосрочной перспективе (например, через 3 месяца) увеличение расходов на рекламу на 1 млн. руб. в настоящий момент времени приведёт к общему росту объёма продаж на 13,14 млн. руб.

Относительные коэффициенты регрессии в этой модели равны:

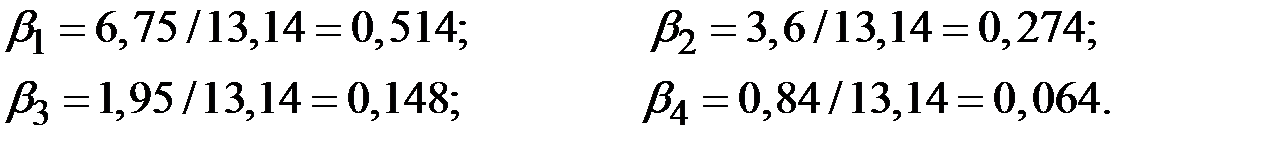
Следовательно, 51,4% общего увеличения объёма продаж, вызванного ростом затрат на рекламу, происходит в текущем моменте времени; 27,4% – в момент ; 14,8% – в момент ; и только 6,4% этого увеличения приходится на момент времени .

Средний лаг в этой модели определяется следующим образом:

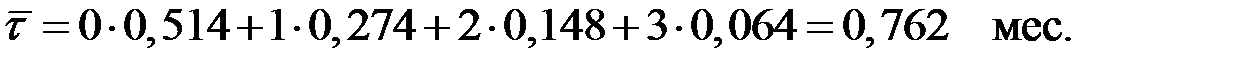
Небольшая величина лага (менее 1 месяца) ещё раз подтверждает, что большая часть эффекта роста затрат на рекламу проявляется сразу же.