Пусть q – выпуск продукции (в натуральных единицах);
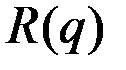 – выручка от продаж;
– выручка от продаж;
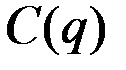 – издержки производства на выпуск q единиц продукции.
– издержки производства на выпуск q единиц продукции.
Тогда прибыль 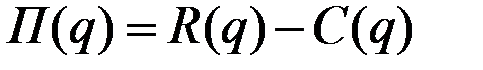 .
.
Предположим, что выполняются следующие условия.
1) Функции 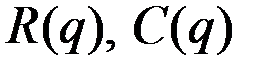 определены на полуинтервале [0, +∞) и дифференцируемы при
определены на полуинтервале [0, +∞) и дифференцируемы при 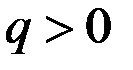 .
.
2) Максимум прибыли достигается в некоторой точке 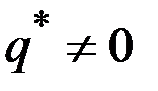 .
.
В случае, когда максимум прибыли 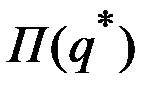 положителен, условие
положителен, условие 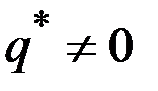 естественным образом выполняется, поскольку
естественным образом выполняется, поскольку 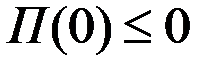 (нет выпуска – нет выручки, нет выручки – нет прибыли).
(нет выпуска – нет выручки, нет выручки – нет прибыли).
Пусть условия 1), 2) выполнены.
Тогда функция 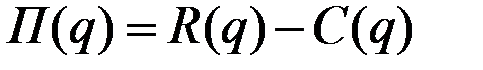 дифференцируема и имеет на интервале [0, +∞) максимум в точке
дифференцируема и имеет на интервале [0, +∞) максимум в точке 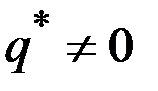 .
.
При этом производная в точке экстремума должна равняться нулю:
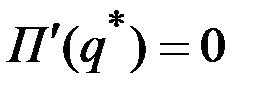 .
.
Так как 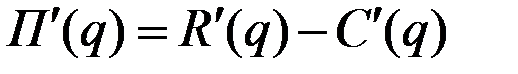 , то в точке
, то в точке 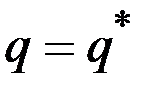 получаем равенство
получаем равенство
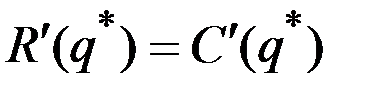 .
.
В экономической теории это равенство объясняется как правило, согласно которому фирма, максимизирующая свою прибыль, устанавливает объём производства таким образом, чтобы предельная выручка была равна предельным издержкам.
Вариант 1. Когда объём производства не влияет на цену продукции (конкурентная фирма), имеем
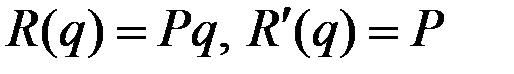 .
.
Тогда 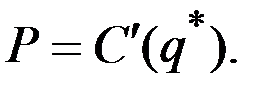
Отсюда можно найти объём выпуска с максимальной прибылью 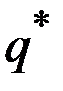 .
.
Пример 4.4. Найти оптимальный объём производства, если известны цена единицы товара и функция совокупных издержек:
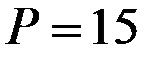 ,
, 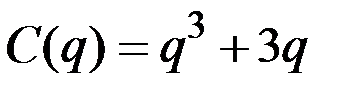 .
.
Решение. Прибыль при производстве q единиц продукции будет
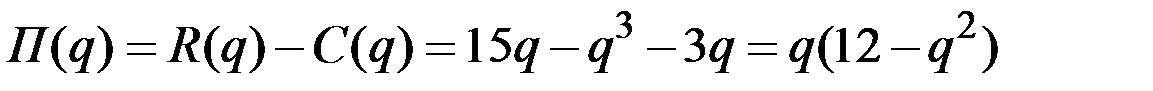 .
.
Очевидно, что 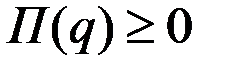 , если
, если 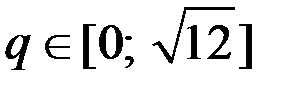 .
.
Так как 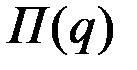 – непрерывная функция, то на отрезке
– непрерывная функция, то на отрезке 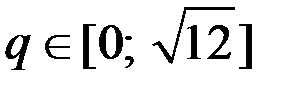 в некоторой точке
в некоторой точке 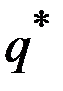 она принимает наибольшее значение на этом отрезке.
она принимает наибольшее значение на этом отрезке.
Поскольку 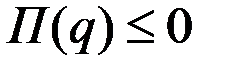 при
при 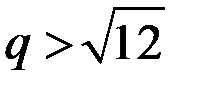 , то
, то 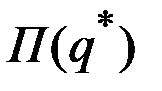 – наибольшее значение при любом
– наибольшее значение при любом 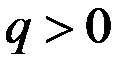 .
.
Тогда из равенства 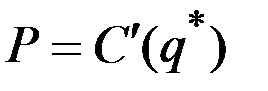 получаем
получаем 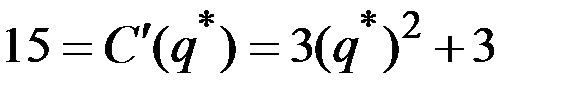 .
.
Отсюда 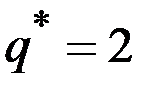 .
.
Так как фирма стремится получить максимальную прибыль, то она будет производить 2 единицы продукции при цене 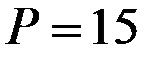
Можно найти функцию предложения 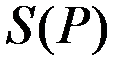 данной фирмы, вычисляя
данной фирмы, вычисляя 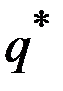 для различных Р:
для различных Р: 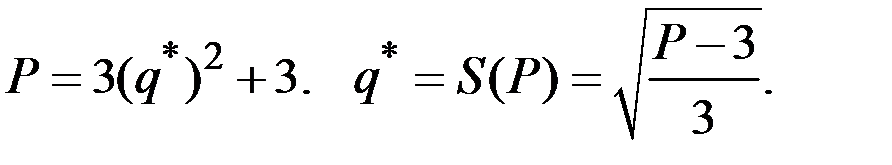
Вариант 2. Рассмотрим более общий случай, когда цена продукции является дифференцируемой функцией 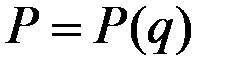 от объёма выпуска q.
от объёма выпуска q.
Имеем выручку 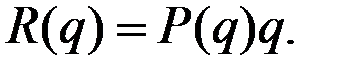
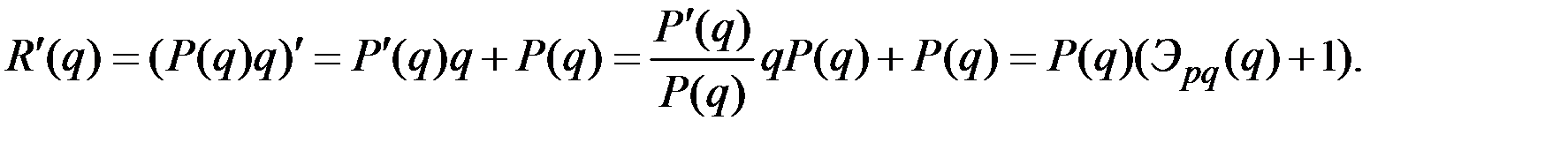
Тогда для оптимального объёма 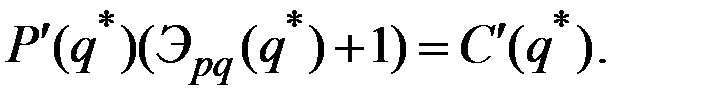
Получим уравнение для оптимальной цены
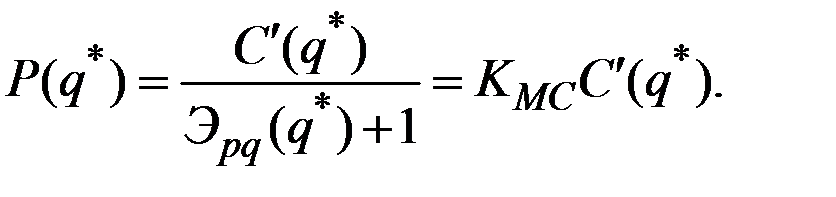
Здесь 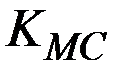 – коэффициент увеличения предельных издержек.
– коэффициент увеличения предельных издержек.
Так как 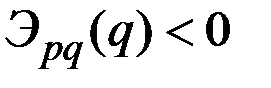 , то из последнего равенства следует, что цена
, то из последнего равенства следует, что цена 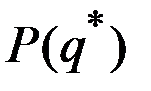 не ниже предельных издержек
не ниже предельных издержек 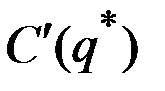 :
: 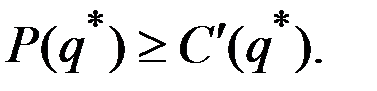
Если фирма занимает существенную долю рынка, то увеличение её выпуска приводит к насыщению рынка и падению цены.
В этом случае 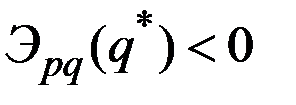 и цена
и цена 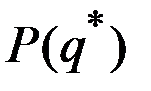 больше издержек
больше издержек 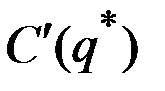 .
.
Вариант 3. Предположим теперь, что фирма является монополией.
В этом случае при цене 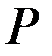 фирма будет производить столько единиц продукции, сколько требуется покупателям при этой цене, т.е.
фирма будет производить столько единиц продукции, сколько требуется покупателям при этой цене, т.е.
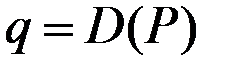 ,
,
где 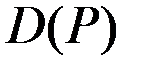 – функция спроса.
– функция спроса.
Таким образом, функция 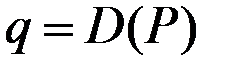 будет обратной функцией для функции
будет обратной функцией для функции 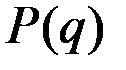 .
.
Из свойств эластичности следует, что
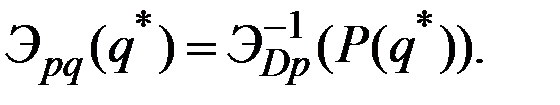
Пусть 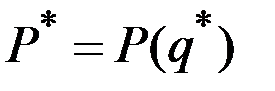 цена, соответствующая выпуску
цена, соответствующая выпуску 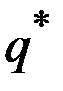 .
.
Оптимальный выпуск 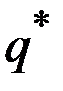 можно представить как спрос при наилучшей (для монополии) цене
можно представить как спрос при наилучшей (для монополии) цене 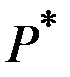 :
: 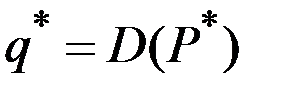 .
.
Уравнение для этой цены приобретает вид
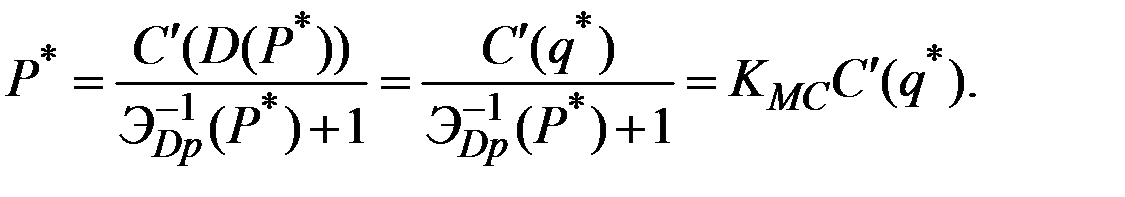
Пусть, например, 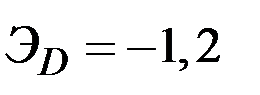 (эластичный спрос).
(эластичный спрос).
Тогда коэффициент увеличения предельных издержек
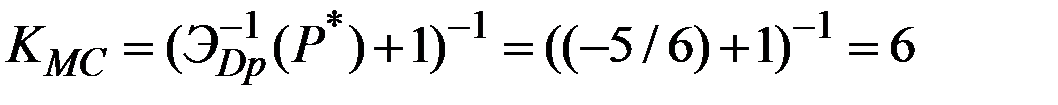 ,
,
т.е. цена монополиста 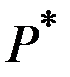 в 6 раз (!) выше его предельных издержек.
в 6 раз (!) выше его предельных издержек.
При неэластичном спросе 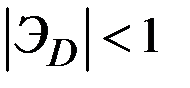 знаменатель дроби в правой части формулы для
знаменатель дроби в правой части формулы для 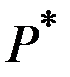 будет отрицательным (
будет отрицательным ( 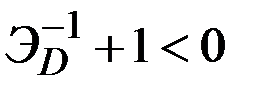 ) и эта формула не имеет смысла.
) и эта формула не имеет смысла.
Это значит, что сделанные ранее предположения невыполнимы.
Фактически, при неэластичном спросе монополия, стремящаяся увеличить свою прибыль, будет снижать объём выпуска. При этом издержки будут снижаться, а цена и прибыль – увеличиваться.
В некоторый момент начнётся массовый отказ (из–за отсутствия средств) потребителей от продукции данной монополии.
Спрос снова станет эластичным.
Пример 4.5. Заданы: переменные издержки фирмы–монополиста 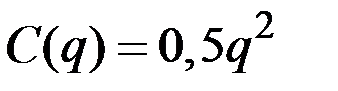 и функция спроса
и функция спроса 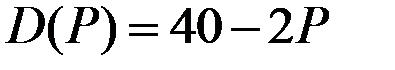 . Найти оптимальный объём производства, соответствующую цену и предельные издержки.
. Найти оптимальный объём производства, соответствующую цену и предельные издержки.
Решение. Так как 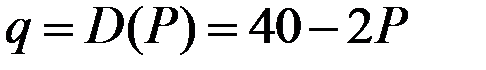 , то
, то
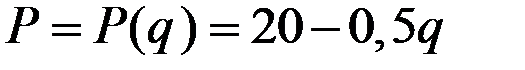 .
.
Для функции 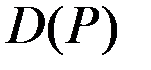 мы нашли обратную функцию
мы нашли обратную функцию 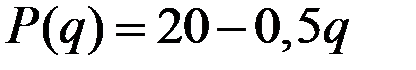 .
.
Прибыль 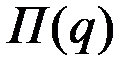 имеет вид
имеет вид
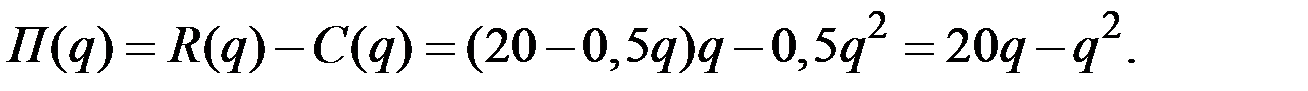
В точке 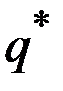 максимума прибыли выполняется равенство
максимума прибыли выполняется равенство
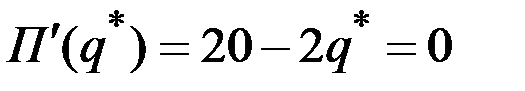 .
.
Находим оптимальный объём производства 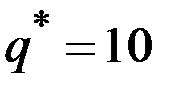 .
.
Соответствующая цена будет равна величине
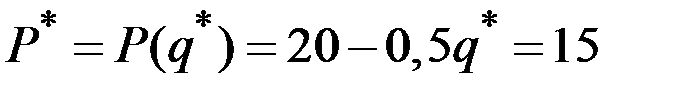 .
.
При этом предельные издержки
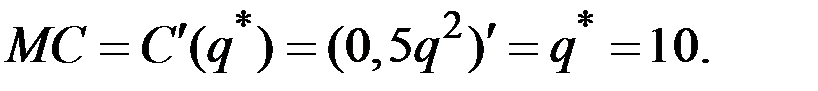
Таким образом, цена, наиболее выгодная для монополии, в полтора раза выше её предельных издержек.
Этот же результат можно получить иначе.
Действительно,
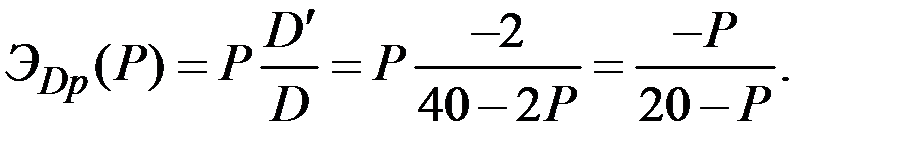
Тогда
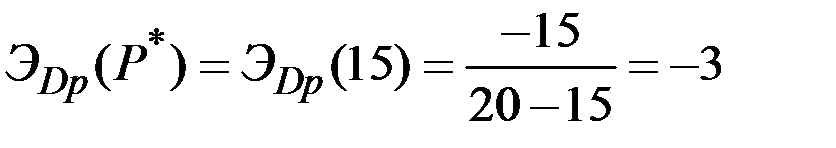 .
.
Следовательно,
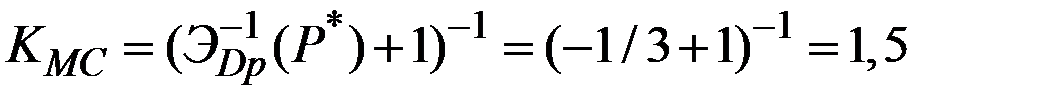 .
.
На практике иногда приходится находить функцию издержек по заданной функции предельных издержек.
В этом случае используем интегрирование.
Пример 4.6. Дана функция предельных издержек
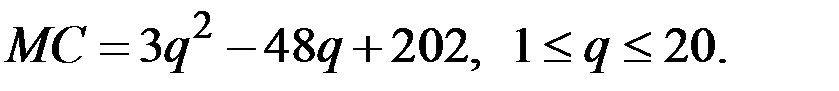
Постоянные издержки равны 50 ден. ед.
Найти функцию издержек 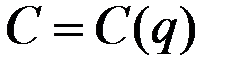 и вычислить издержки в случае производства 10 единиц товара.
и вычислить издержки в случае производства 10 единиц товара.
Решение. Функцию издержек находим интегрированием:
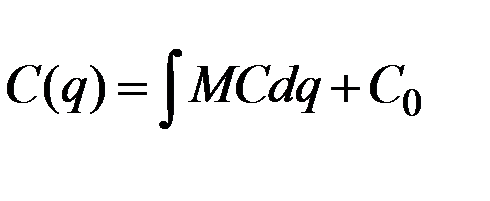
где константа 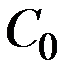 , находится из данного условия
, находится из данного условия 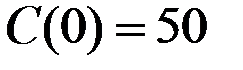 , так что
, так что 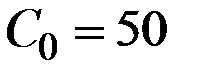 , поскольку интеграл при q = 1 обращается в нуль.
, поскольку интеграл при q = 1 обращается в нуль.
Интегрируя, получим функцию издержек
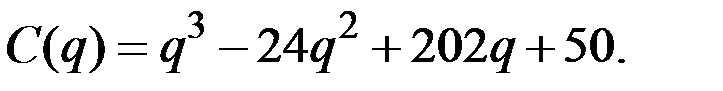
Подставляя сюда q = 10, находим искомое значение
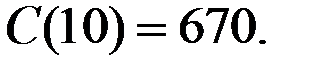
Дата: 2019-03-05, просмотров: 482.