Простейший метод прогнозирования показателя – это усреднение q его прошлых значений (скользящее среднее):
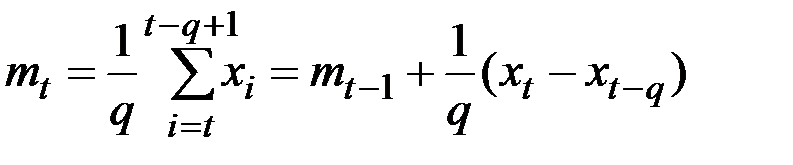 .
.
Вычисленное значение 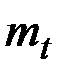 полагается равным прогнозу ожидаемого будущего значения стационарного показателя Х.
полагается равным прогнозу ожидаемого будущего значения стационарного показателя Х.
Эта простейшая модель находится у истоков адаптивного направления методов прогнозирования. Модификации и обобщения этой модели привели к появлению целого семейства адаптивных моделей с различными свойствами.
В основе процедуры адаптации лежит метод проб и ошибок, который считается универсальным путём выработки нового поведения.
Особенностью и недостатком скользящего среднего является то, что здесь всем данным, включённым в процесс, присваивается одинаковый вес 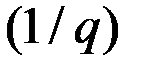 , показывающий долю вклада каждого наблюдения в значение среднего.
, показывающий долю вклада каждого наблюдения в значение среднего.
Чтобы учесть большую значимость более «свежих» данных, можно ввести систему весов, например, убывающих во времени по экспоненциальному закону: 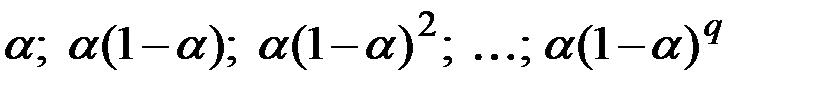 .
.
Сумма ряда стремится к единице, а члены ряда убывают со временем. Например, для 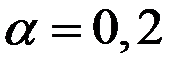 весовые коэффициенты данных с удалением от текущего момента убывают следующим образом:
весовые коэффициенты данных с удалением от текущего момента убывают следующим образом:
0,2; 0,16; 0,128; 0,102; 0,082 и т.д.
Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле
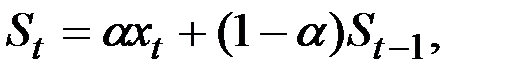
где 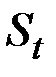 – значение экспоненциальной средней в момент
– значение экспоненциальной средней в момент 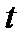 ;
;
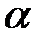 – параметр сглаживания,
– параметр сглаживания, 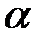 = const, 0 <
= const, 0 < 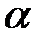 < 1.
< 1.
Это выражение можно переписать следующим образом:

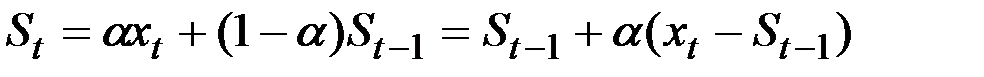 .
.
Экспоненциальная средняя на момент t здесь выражена как экспоненциальная средняя предшествующего момента плюс доля a разницы текущего наблюдения и экспоненциальной средней прошлого момента.
Если последовательно использовать записанное рекуррентное соотношение, то экспоненциальную среднюю 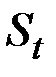 можно выразить через значения временного ряда
можно выразить через значения временного ряда 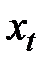 :
:
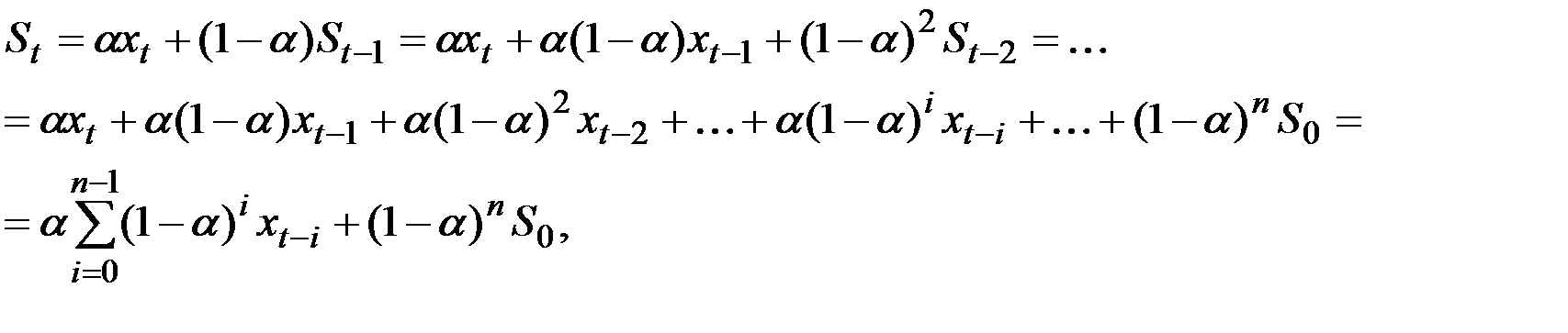
где n – количество членов ряда;
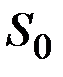 – некоторая величина, характеризующая начальные условия для первого применения формулы при t = 1.
– некоторая величина, характеризующая начальные условия для первого применения формулы при t = 1.
Так как 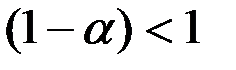 , то при
, то при 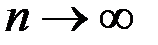 величина
величина 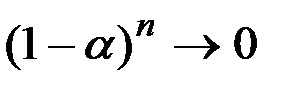 , а сумма коэффициентов
, а сумма коэффициентов 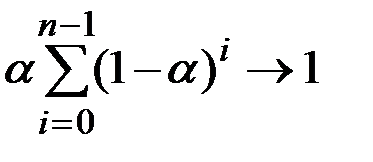 .
.
Тогда
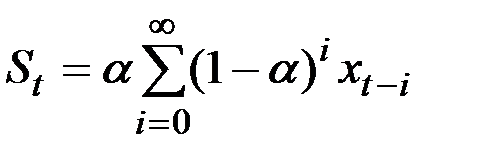 .
.
Таким образом, величина 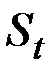 оказывается взвешенной суммой всех членов ряда. Причём веса падают экспоненциально в зависимости от давности наблюдения. Это и объясняет, почему величина
оказывается взвешенной суммой всех членов ряда. Причём веса падают экспоненциально в зависимости от давности наблюдения. Это и объясняет, почему величина 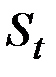 названа экспоненциальной средней.
названа экспоненциальной средней.
Между параметром 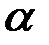 и числом значения ряда
и числом значения ряда 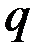 в процедуре скользящего среднего существует соотношение (обеспечивающее одинаковую чувствительность прогноза к новым данным):
в процедуре скользящего среднего существует соотношение (обеспечивающее одинаковую чувствительность прогноза к новым данным):
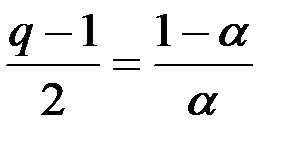 .
.
Так значение 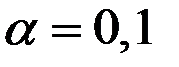 эквивалентно усреднению 19 членов ряда в скользящем среднем,
эквивалентно усреднению 19 членов ряда в скользящем среднем, 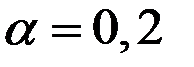 эквивалентно
эквивалентно 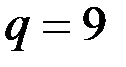 ,
, 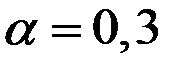 обеспечивает ту же чувствительность прогноза к обновлению данных, что и
обеспечивает ту же чувствительность прогноза к обновлению данных, что и 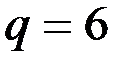 .
.
Рассмотрим ряд, генерированный моделью
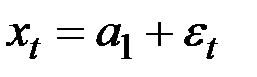 ,
,
где 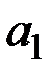 = const;
= const;
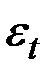 – случайные неавтокоррелированые отклонения или шум со средним значением 0 и дисперсией
– случайные неавтокоррелированые отклонения или шум со средним значением 0 и дисперсией 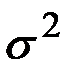 .
.
Применим к ряду процедуру экспоненциального сглаживания.
Тогда
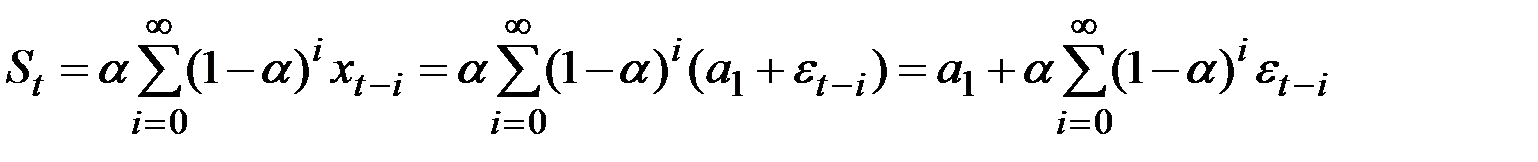 .
.
Найдём математическое ожидание
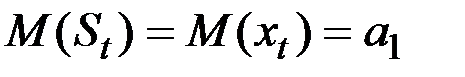
и дисперсию величины 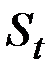
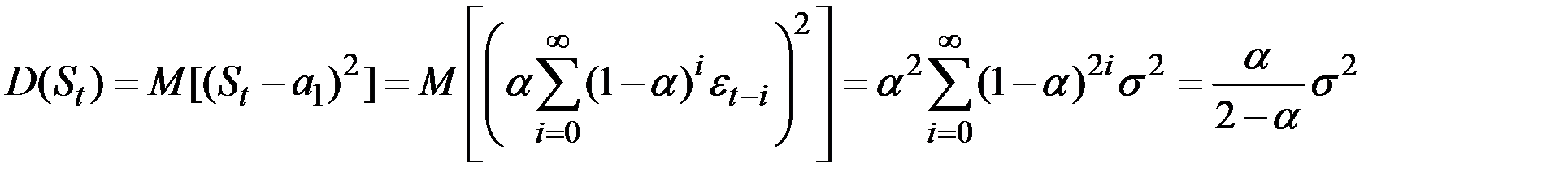 .
.
Так как 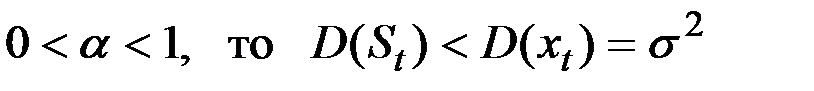 .
.
Таким образом, экспоненциальная средняя 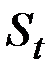 имеет то же математическое ожидание, что и исходный ряд
имеет то же математическое ожидание, что и исходный ряд 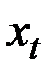 , но меньшую дисперсию.
, но меньшую дисперсию.
При высоком значении a дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда 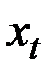 .
.
Чем меньше a, тем в большей степени сокращается дисперсия экспоненциальной средней.
Следовательно, экспоненциальное сглаживание можно представить как фильтр, на вход которого в виде потока последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней. И чем меньше a, тем в большей степени фильтруются, подавляются колебания исходного ряда.
Экспоненциальная средняя часто используется для краткосрочного прогнозирования.
В этом случае предполагается, что ряд генерируется моделью
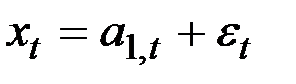 ,
,
где 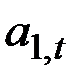 – варьирующий во времени средний уровень ряда;
– варьирующий во времени средний уровень ряда;
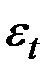 – случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией
– случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией 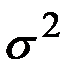 .
.
Прогнозная модель имеет вид
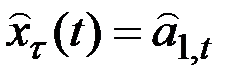 ,
,
где 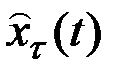 – прогноз, сделанный в момент t на t единиц времени вперёд;
– прогноз, сделанный в момент t на t единиц времени вперёд;
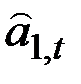 – оценка параметра тренда
– оценка параметра тренда 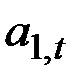 .
.
Средством оценки единственного параметра модели служит экспоненциальная средняя
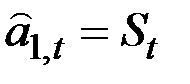 .
.
Таким образом, все свойства экспоненциальной средней распространяются на прогнозную модель.
В частности, если 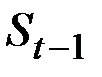 рассматривать как прогноз на 1 шаг вперёд, то величина
рассматривать как прогноз на 1 шаг вперёд, то величина 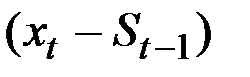 есть погрешность этого прогноза, а новый прогноз
есть погрешность этого прогноза, а новый прогноз 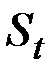 получается в результате корректировки предыдущего прогноза с учётом его ошибки. В этом и состоит суть адаптации.
получается в результате корректировки предыдущего прогноза с учётом его ошибки. В этом и состоит суть адаптации.
При краткосрочном прогнозировании желательно как можно быстрее отразить изменения 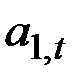 и в то же время как можно лучше очистить ряд от случайных колебаний. С одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением a, с другой стороны, для сглаживания случайных отклонений величину a нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения a составляет задачу оптимизации модели.
и в то же время как можно лучше очистить ряд от случайных колебаний. С одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением a, с другой стороны, для сглаживания случайных отклонений величину a нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения a составляет задачу оптимизации модели.
Чувствительность экспоненциально взвешенного среднего в целях повышения адекватности прогностической системы может быть в любой момент изменена путём корректировки величины 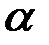 . Чем выше
. Чем выше 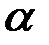 , тем выше чувствительность среднего к поступающим новым данным.
, тем выше чувствительность среднего к поступающим новым данным.
Чем ниже 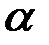 , тем устойчивее становится среднее.
, тем устойчивее становится среднее.
Накопленный опыт исследования экономических рядов и анализ литературных источников свидетельствуют о целесообразных границах для 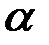 (при прочих равных условиях): 0,1 ¸ 0,3.
(при прочих равных условиях): 0,1 ¸ 0,3.
Использование модели предполагает решение трёх вопросов.
1. Выбор константы сглаживания 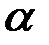 .
.
2. Выбор начального уровня сглаживания ряда 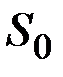 , так как на первом шаге необходимо вычислить первое приближение среднего
, так как на первом шаге необходимо вычислить первое приближение среднего
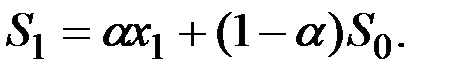
Здесь возможные следующие варианты: в качестве 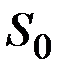 можно взять первый член ряда:
можно взять первый член ряда: 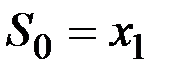 ; в качестве
; в качестве 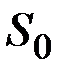 можно взять среднее несколько первых или предыдущих членов ряда; для стационарного ряда в качестве
можно взять среднее несколько первых или предыдущих членов ряда; для стационарного ряда в качестве 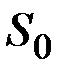 можно взять среднее значение ряда.
можно взять среднее значение ряда.
3. Выбор начального момента сглаживания, т.е. длины базы сглаживания или прогноза. Эта задача тесно связана с первой, т.е. с выбором параметра 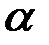 .
.
Аналитического решения поставленных задач не существует.
Выбор характеристик сглаживания часто основывается на экспериментальных расчётах.
Часто практикуется метод обучающей выборки для экспериментальной проверки качества прогнозирования.
При этом имеющийся ряд 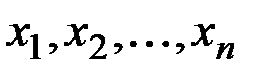 разбивается на две части: обучающую выборку
разбивается на две части: обучающую выборку 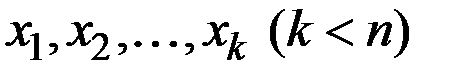 и экзаменующую выборку
и экзаменующую выборку 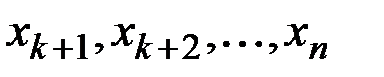 .
.
На обучающем ряде оцениваем все необходимые параметры, а на экзаменующем смотрим, насколько наша прогностическая модель хорошо предсказывает фактические значения показателя.
Основная проблема при этом – найти оптимальное значение 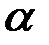 .
.
При поиске оптимального значения 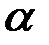 можно задать сетку значений для
можно задать сетку значений для 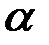 , например,
, например, 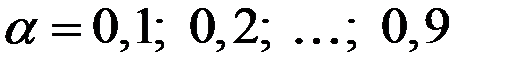 .
.
Для каждого из этих значений сгладим ряд 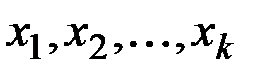 .
.
Тогда прогноз на момент времени 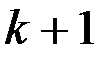 есть
есть 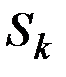 , а ошибкой прогноза будет величина
, а ошибкой прогноза будет величина 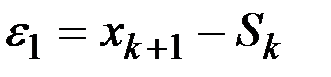 .
.
Далее сдвигаем базу данных для прогноза на единицу вправо, т.е. сгладим ряд 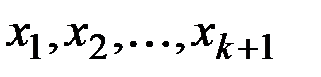 .
.
Ошибка прогноза в этом случае будет равна 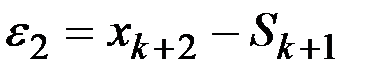 .
.
Таким способом будет построено 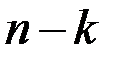 ошибок прогноза.
ошибок прогноза.
Можно найти какую–то среднюю ошибку прогноза по всей экзаменующей части ряда, например, 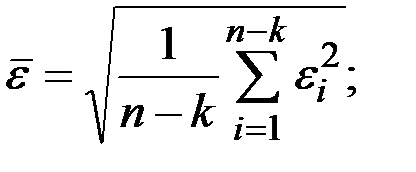
или 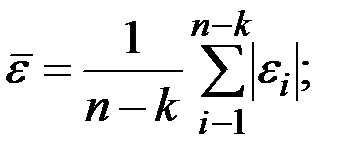 или
или 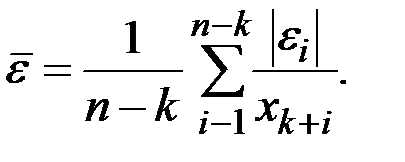
Проигрывая таким образом прогнозируемые ситуации, можно найти то значение 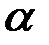 , которое обращает в минимум выбранный функционал качества прогноза. Аналогично можно оптимальным образом подбирать и длину базы
, которое обращает в минимум выбранный функционал качества прогноза. Аналогично можно оптимальным образом подбирать и длину базы 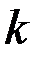 , и начальный уровень сглаживания
, и начальный уровень сглаживания 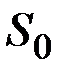 .
.
Дата: 2019-03-05, просмотров: 768.