Для адекватности модели ряд остатков 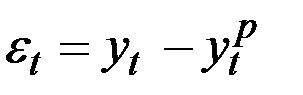 должен обладать свойствами:

1) случайности,

2) независимости последовательности уровней,

3) нормальности распределения.

2.1. Проверку случайности уровней остатков ряда проводим на основе критерия поворотных точек. Для этого каждый уровень ряда остатков сравниваем с двумя соседними.

Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в соответствующей строчке табл. 5.4 ставится 1, в противном случае ставится 0.

В первой и последней строке ставится прочерк, т.к. у этих уровней нет двух соседних точек.

Общее число поворотных точек в примере равно .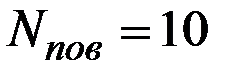 

Рассчитаем значение критерия поворотных точек как целую часть выражения:

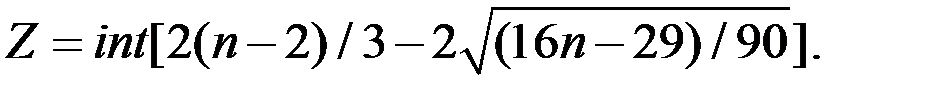
При 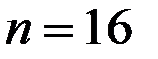 получаем:

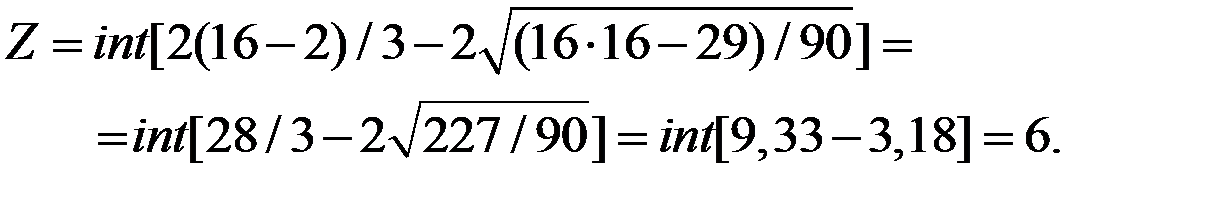
Если количество поворотных точек 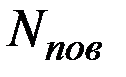 больше 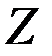, то условие случайности выполнено.

В нашем случае

.

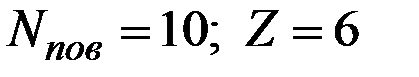Это означает, что условие случайности выполнено.

2.2. Проверка отсутствия автокорреляции (независимости уровней остатков).

Эту проверку проведём двумя методами:

1) по критерию Дарбина–Уотсона;

2) по первому коэффициенту автокорреляции.

1. Вычислим значение критерия Дарбина–Уотсона:

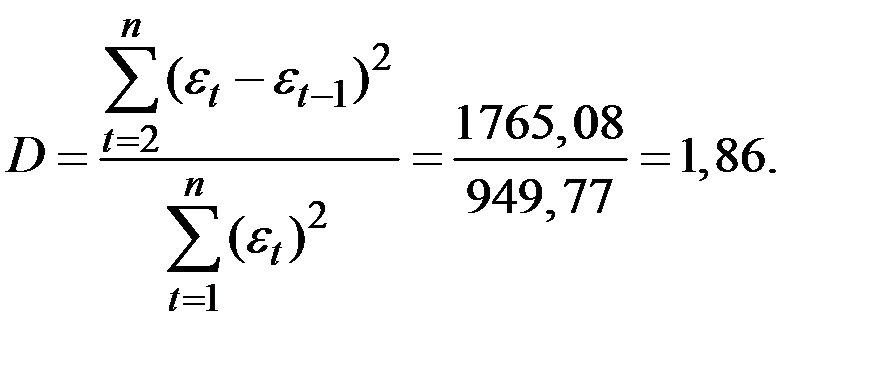
Полученное значение критерия сравнивают с критическими точками 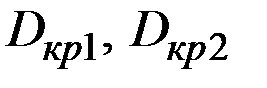, взятыми из соответствующих таблиц.

В нашем случае 

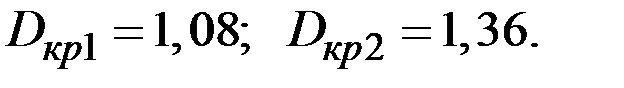
Если 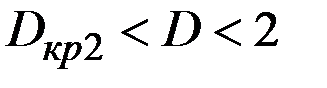, то уровни ряда остатков являются независимыми.

В нашем случае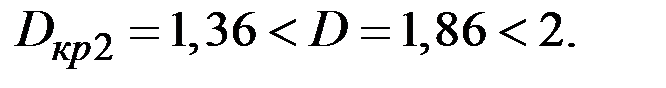   

Следовательно, уровни ряда остатков являются независимыми. 

2. Вычислим первый коэффициент автокорреляции по формуле

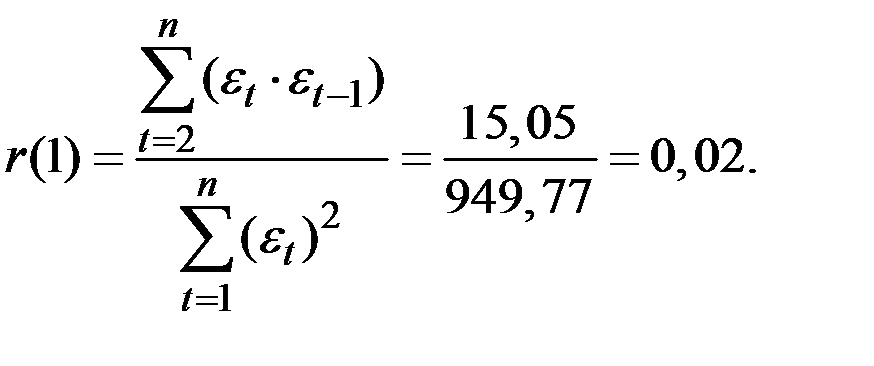
Если модуль вычисленного первого коэффициента автокорреляции меньше критического значения 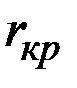 (которое можно взять из соответствующей таблицы), то уровни остатков ряда будут независимы.

У нас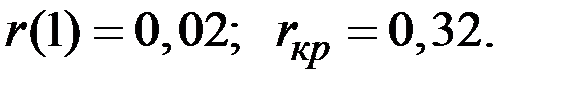

Следовательно, уровни ряда остатков являются независимыми.

2.3. Проверим соответствие ряда остатков нормальному распределению по 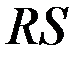 – критерию.

Рассчитаем значение 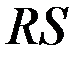 – критерия по формуле:

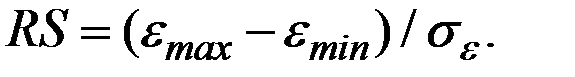
Здесь 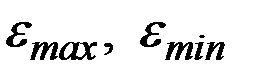 – максимальное и минимальное значения уровней ряда остатков, а  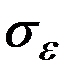– среднее квадратическое отклонение ряда остатков.

Имеем:

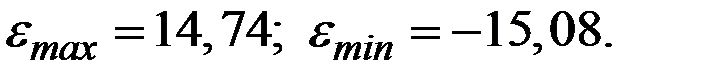
Среднее квадратическое отклонение ряда остатков вычислим по формуле

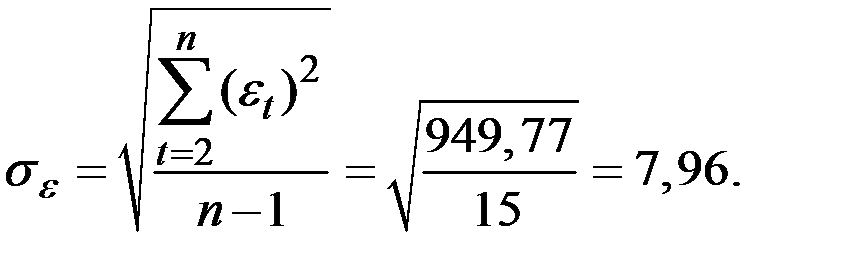
Рассчитаем значение 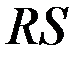 – критерия по формуле:

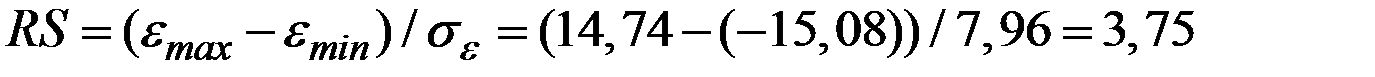
Полученное значение критерия сравнивают с табличными значениями, которые зависят от количества точек и уровня значимости.

Для уровня значимости 5% и числа точек 16 полученное значение 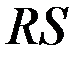 для нормального распределения должно находиться в интервале от 3,00 до 4,21.

Так как 3,00 < 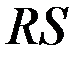 =3,75 < 4,21, то ряд остатков подчиняется нормальному распределению.

Все условия адекватности и точности выполнены. Можно говорить о возможности прогноза показателя на 4 квартала вперёд.