К прогнозированию показателей можно идти двумя путями.

1. Попытаться вскрыть причинно–следственный механизм процесса, т.е. найти факторы, определяющие поведение показателя, прогноз по которым легко найти. Этот путь приводит к построению модели поведения экономического объекта.

2. Попытаться предсказать будущее значение показателя, анализируя временной ряд этого показателя.

Обычно предполагается, что ряд 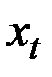 генерируется моделью, состоящей минимум из двух компонент:

,

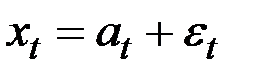где величина 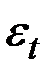 генерируется случайным неавтокоррелированым процессом с нулевым средним значением и конечной (не обязательно постоянной) дисперсией, а величина  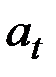может быть генерирована либо детерминированной функцией, либо случайным процессом, либо какой–нибудь их комбинацией.

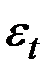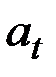Величины  и  различаются характером воздействия на значения последующих значений ряда.

Именно величина 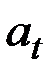 характеризует уровень ряда в момент времени t и в основном определяет поведение последующих членов ряда, т.е. тренд (эволюцию уровня ряда во времени).

Компоненты ряда 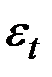 и 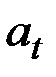 не наблюдаемы. Они являются теоретическими величинами. Их выделение (нахождение) и составляет предмет анализа временного ряда в задаче прогнозирования.

Оценку будущих членов ряда обычно делают по прогнозной модели.

Прогнозная модель – это модель, аппроксимирующая тренд.

Прогнозы – это расчёт будущих уровней ряда, а последовательность прогнозов для различных периодов упреждения t составляет оценку тренда.

Различные методы прогнозирования базируются на различных гипотезах генерирования составляющих временного ряда.

Прежде всего, необходимо провести предварительный анализ исходного ряда. На этом шаге могут быть выделены некоторые его основные характеристики: наличие выбросов, сезонности и т.д.

На этом этапе может быть произведён и предварительный выбор прогнозной модели.

Отметим, что при проведении предварительного анализа необходимо рассматривать исходный ряд со всеми его особенностями.

Большинство моделей прогнозирования предъявляют достаточно жёсткие требования к исходному ряду, требуя его стационарности и однородности его основных характеристик. Поэтому перед проведением прогнозирования производится ряд преобразований исходного ряда, цель которых – привести ряд к оптимальному для модели виду.

После выполнения прогнозирования эти преобразования в обратном порядке применяются к построенной модели.

Помимо данных исходного ряда, прогнозные модели могут использовать вспомогательные временные ряды, так или иначе описывающие внешние условия, в которых происходит изменение исследуемого показателя. Это корректирующие ряды, регрессоры, ряды интервенций, сезонные факторы и так далее.

Регрессор представляет собой временной ряд, моменты времени наблюдений которого совпадают с соответствующими моментами времени исходного ряд. Этот ряд должен отражать изменение показателя, достаточно сильно связанного с исследуемым.

Многие модели, в частности модель авторегрессии и скользящего среднего (АРИСС), позволяют вычислять значения прогноза исходного ряда основываясь не только на прошлых значениях этого ряда, но и на прогнозных значениях рядов регрессоров.

В том случае, если регрессор хорошо прогнозируется некоторой прогнозной моделью, его использование может улучшить качество прогноза. Корректирующий ряд, в отличие от регрессора, не требует подгонки какой–либо модели.

Значения корректирующего ряда просто вычитаются из исходного ряда перед проведением оценки, построения модели и прогнозирования.

После проведения прогнозирования значения корректирующего ряда добавляются к прогнозным значениям.

Корректирующий ряд можно использовать для учёта возможных в будущем событий, которые никогда не происходили в прошлом, и, следовательно, не могут быть учтены регрессионной моделью.

Такая ситуация может, например, возникнуть, если мы прогнозируем объём продаж какого–то товара и знаем, что в ближайшем будущем планируется широкая рекламная кампания по продвижению этого товара.

Однако, если такие акции планируется проводить и в дальнейшем, имеет смысл учитывать их эффект в виде временного ряда – регрессора.