1. Коэффициент автокорреляции строится по аналогии с линейным коэффициентом корреляции и характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых рядов, имеющих сильную нелинейную тенденцию (параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Автокорреляционная функция (АКФ) ряда – последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков.
График зависимости её значений от величины лага τ (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ АКФ и коррелограммы позволяет исследовать структуру ряда, т.е. определить лаг, при котором автокорреляция наиболее тесная.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции порядка t, ряд содержит циклические колебания с периодичностью в t моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда:
1) либо ряд не содержит тенденции и циклических колебаний и имеет только случайную составляющую;
2) либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Коэффициент автокорреляции уровней и АКФ целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой и циклической (сезонной) составляющих.
Если основной тренд ряда динамики выявлен и описан математически, то с помощью построенной функции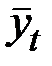 
можно осуществлять прогнозирование, то есть распространить выявленные закономерности развития изучаемого явления на будущее (экстраполирование).
Основой прогнозирования является предположение о том, что закономерность, действующая внутри анализируемого ряда динамики, сохраняется и в дальнейшем.
Для расчёта прогнозных значений необходимо на трендовую составляющую 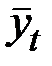наложить сезонную составляющую 
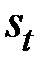(если она есть), то есть расчёт следует проводить по модели 
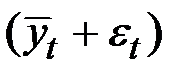или 
.
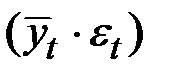Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.
Простейший подход – расчёт значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, то строят мультипликативную модель ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчёту значений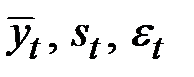 
для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчёт значений сезонной компоненты.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных 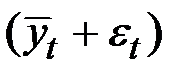в аддитивной или 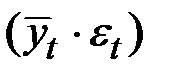в мультипликативной модели.
4. Аналитическое выравнивание уровне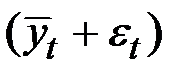й или 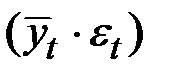и расчёт значений 
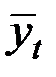с использованием полученного уравнения тренда.
5. Расчёт полученных по модели значени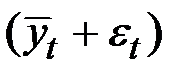й или .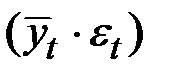
6. Расчёт абсолютных и (или) относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать ряд ошибок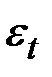 
для анализа взаимосвязи исходного ряда и других рядов.
Пример 5.3. Имеются данные об объёмах потребления электроэнергии жителями города за 18 кварталов (табл. 5.5). Различными методами спрогнозировать потребление электроэнергии жителями города на ближайшие полгода.
Решение. Исследуем структуру этого ряда.
Определим коэффициенты автокорреляции различных порядков.
Таблица 5.5
Потребление электроэнергии жителями города, млн. кВт·ч
| 
|  
| 
| 
| 
|
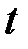
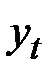
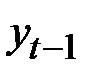
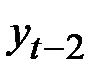
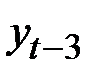
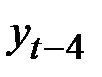
| 1 | 30 | ||||
| 2 | 22 | 30 | |||
| 3 | 25 | 22 | 30 | ||
| 4 | 45 | 25 | 22 | 30 | |
| 5 | 36 | 45 | 25 | 22 | 30 |
| 6 | 24 | 36 | 45 | 25 | 22 |
| 7 | 30 | 24 | 36 | 45 | 25 |
| 8 | 50 | 30 | 24 | 36 | 45 |
| 9 | 48 | 50 | 30 | 24 | 36 |
| 10 | 28 | 48 | 50 | 30 | 24 |
| 11 | 32 | 28 | 48 | 50 | 30 |
| 12 | 55 | 32 | 28 | 48 | 50 |
| 13 | 45 | 55 | 32 | 28 | 48 |
| 14 | 33 | 45 | 55 | 32 | 28 |
| 15 | 35 | 33 | 45 | 55 | 32 |
| 16 | 54 | 35 | 33 | 45 | 55 |
| 17 | 42 | 54 | 35 | 33 | 45 |
| 18 | 30 | 42 | 54 | 35 | 33 |
Значения АКФ этого ряда и коррелограмма приведены в табл. 5.6.
Коэффициент автокорреляции первого порядка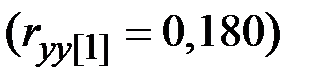 
свидетельствует о слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Структура ряда такова, что каждый следующий уровень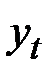 
зависит от уровня 
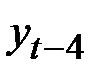и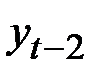 
в гораздо большей степени, чем от уровня 
.
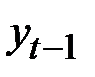Анализ значений АКФ позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в четыре квартала.
Данный вывод подтверждается и графическим анализом структуры ряда.
Таблица 5.6
Коррелограмма временного ряда потребления электроэнергии
| Лаг τ | Коэффициенты автокорреляции уровней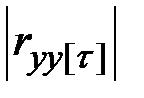 
| Коррелограмма |
| 1 | 0,1802 | ** |
| 2 | 0,6115 | ******* |
| 3 | 0,1237 | * |
| 4 | 0,9190 | ************ |
| 5 | 0,0884 | |
| 6 | 0,7718 | ********* |
| 7 | 0,0208 | |
| 8 | 0,8171 | *********** |
| 9 | 0,0698 |
1. Построим аддитивную модель ряда потребления электроэнергии жителями города за 4,5 года.
Данный ряд содержит сезонные колебания периодичностью 4.
Объёмы потребления электроэнергии в осенне–зимний период времени (I и IV кварталы) выше, чем весной и летом (II и III кварталы).
По графику этого ряда можно установить наличие приблизительно равной амплитуды колебаний.
Это свидетельствует о возможном существовании аддитивной модели временного ряда.
Рассчитаем её компоненты.
Шаг 1. Проведём выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр.3 табл. 5.7);
2) разделив полученные суммы на 4, найдём скользящие средние (гр.4 табл. 5.7). Полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних, т.е. центрированные скользящие средние (гр.5 табл. 5.7).
Таблица 5.7
Расчёт оценок сезонной компоненты в аддитивной модели
№
квар–тала,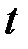 
| Потребление электро–энергии,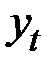 
| Итого по 4 кварталам | Скользящая средняя по кварталам | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | 30 22 25 45 36 24 30 50 48 28 32 55 45 33 35 54 42 30 | 122 128 130 135 140 152 156 158 163 160 165 168 167 164 161 | 30,50 32,00 32,50 33,75 35,00 38,00 39,00 39,50 40,75 40,00 41,25 42,00 41,75 41,00 40,25 | 31,250 32,250 33,125 34,375 36,500 38,500 39,250 40,125 40,375 40,625 41,625 41,875 41,375 40,625 | –6,250 12,750 2,875 –10,375 –6,500 11,500 8,750 –12,125 –8,375 14,375 3,375 –8,875 –6,375 13,375 |
Шаг 2. Найдём оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр.6 табл. 5.7).
Найдём (табл. 5.8) средние за каждый квартал (по всем годам) оценки сезонной компоненты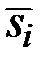 
.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются.
В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю:
.
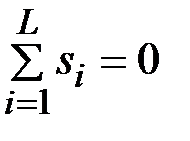Для данной модели имеем:
.
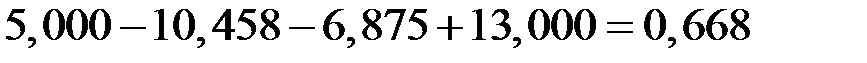Определим корректирующий коэффициент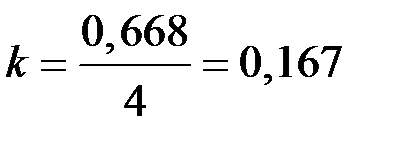 
.
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
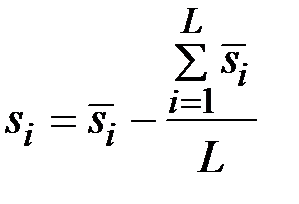, где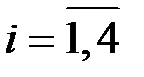 
.
Проверим условие равенства нулю суммы значений сезонной компоненты:
.
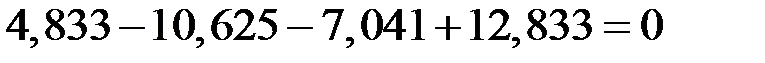Таким образом, получены следующие значения сезонной компоненты по кварталам года:
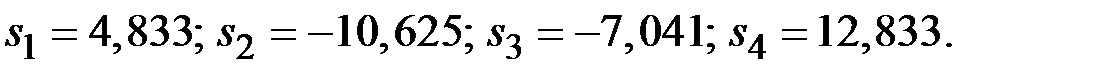
Занесём полученные значения в табл. 5.9 для соответствующих кварталов каждого года (гр.3 табл. 5.9).
Таблица 5.8
Расчёт значений сезонной компоненты в аддитивной модели
| Показатели | № квартала, i | |||
| I | II | III | IV | |
| Сезонная компонента 1–го года | –6,250 | 12,750 | ||
| Сезонная компонента 2–го года | 2,875 | –10,375 | –6,500 | 11,500 |
| Сезонная компонента 3–го года | 8,750 | –12,125 | –8,375 | 14,375 |
| Сезонная компонента 4–го года | 3,375 | –8,875 | –6,375 | 13,375 |
| Итого за i–й квартал (за все годы) | 15,000 | –31,375 | –25,500 | 52,000 |
Средняя оценка сезонной
компоненты для i–го квартала,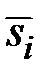 
| 5,000 | –10,458 | –6,875 | 13,000 |
Скорректированная сезонная
компонента,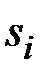 
| 4,833 | –10,625 | –5,041 | 12,833 |
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая её значение из каждого уровня исходного ряда.
Получим величины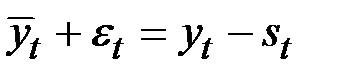 
(гр.4 табл. 5.9).
Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту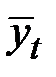 
данной модели.
Для этого проведём аналитическое выравнивание ряда (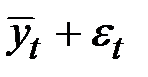 
) с помощью линейного тренда.
Результаты аналитического выравнивания следующие:
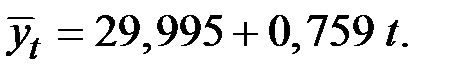
Подставляя в это уравнение значения t = 1, ..., 18, найдём уровни 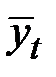для каждого момента времени (гр.5 табл. 5.9).
Шаг 5. Найдём значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням тренда значения сезонной компоненты для соответствующих кварталов .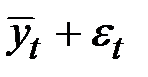
Таблица 5.9
Расчёт выравненных значений тренда и ошибок в аддитивной модели
| t |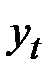 
| 
| 
| 
| 
| 
| 
|
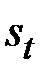
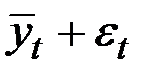
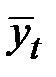
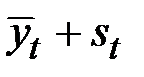
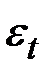
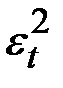
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 30 | 4,833 | 25,167 | 30,756 | 35,589 | –5,589 | 31,237 |
| 2 | 22 | 10,625 | 32,625 | 31,515 | 20,890 | 1,110 | 1,232 |
| 3 | 25 | –5,041 | 32,041 | 32,274 | 25,233 | –0,233 | 0,054 |
| 4 | 45 | 12,833 | 32,167 | 33,033 | 45,866 | –0,866 | 0,750 |
| 5 | 36 | 4,833 | 31,167 | 33,792 | 38,625 | –2,625 | 6,891 |
| 6 | 24 | –10,625 | 34,625 | 34,551 | 23,926 | 0,074 | 0,005 |
| 7 | 30 | –5,041 | 35,041 | 35,310 | 28,269 | 1,731 | 2,996 |
| 8 | 50 | 12,833 | 35,167 | 36,069 | 48,902 | 1,098 | 1,206 |
| 9 | 48 | 4,833 | 43,167 | 36,828 | 41,661 | 6,339 | 40,183 |
| 10 | 28 | –10,625 | 38,625 | 35,587 | 26,962 | 1,038 | 1,077 |
| 11 | 32 | –5,041 | 39,041 | 38,346 | 31,305 | 0,695 | 0,483 |
| 12 | 55 | 12,833 | 42,167 | 39,105 | 51,938 | 3,062 | 9,376 |
| 13 | 45 | 4,833 | 40,167 | 39,864 | 44,697 | 0,303 | 0,092 |
| 14 | 33 | –10,625 | 43,625 | 40,623 | 29,998 | 3,002 | 9,012 |
| 15 | 35 | –5,041 | 42,041 | 41,382 | 34,341 | 0,659 | 0,434 |
| 16 | 54 | 12,833 | 41,167 | 42,141 | 54,974 | –0,974 | 0,949 |
| 17 | 42 | 4,833 | 35,167 | 42,900 | 45,733 | –5,733 | 32,867 |
| 18 | 30 | –10,625 | 40,625 | 43,659 | 33,034 | –3,034 | 9,205 |
Шаг 6. В соответствии с методикой построения аддитивной модели расчёт ошибки производится по формуле
.
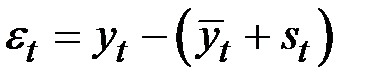Это абсолютная ошибка.
Численные значения абсолютных ошибок приведены в гр.7 табл. 5.9.
По аналогии с моделью регрессии для оценки качества построенной модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок.
Для данной аддитивной модели сумма квадратов абсолютных ошибок равна
.
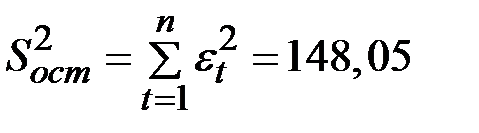Среднее значение уровней исходного ряда:
.
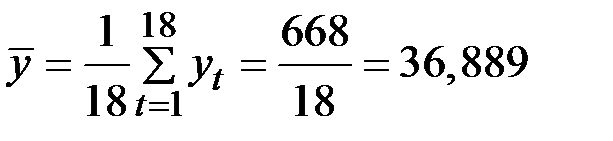Общая сумма квадратов отклонений уровней ряда от его среднего уровня:
.
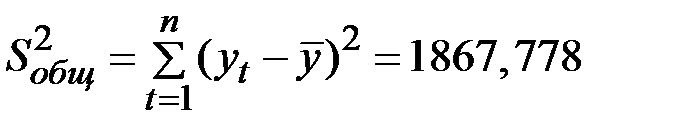Коэффициент детерминации равен
.
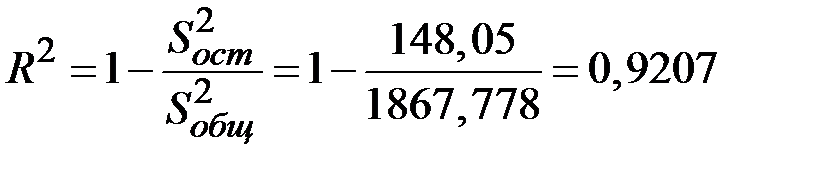Аддитивная модель объясняет 92,07% общей вариации уровней ряда потребления электроэнергии за последние 18 кварталов.
Шаг 7. Спрогнозируем потребление электроэнергии жителями города в течение второго полугодия последнего года по аддитивной модели ряда.
Прогнозное значение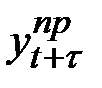 
уровня ряда в аддитивной модели есть сумма трендовой и сезонной составляющих.
Объём электроэнергии, потреблённой в течение второго полугодия пятого года, рассчитывается как сумма объёмов потребления электроэнергии в III и в IV кварталах пятого года, соответственно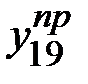 
и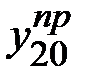 
.
Для определения трендовой компоненты воспользуемся уравнением тренда
.
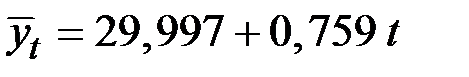Получим
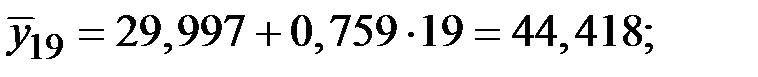
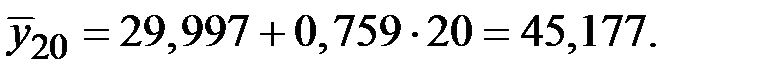
Значения сезонной компоненты равны
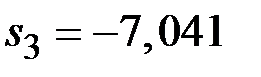(IΙΙ квартал); 
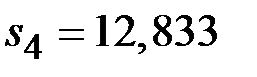(IV квартал).
Таким образом,
.
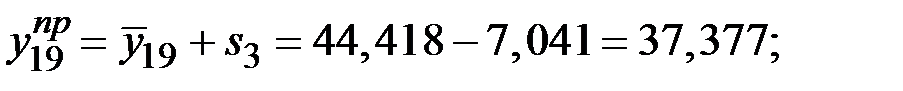
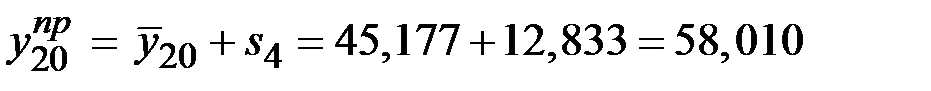Прогноз объёма потребления электроэнергии на второе полугодие последнего года составит
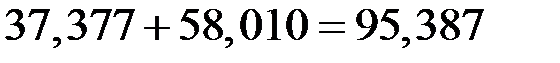млн. кВт·ч.
2. Построим мультипликативную модель ряда.
Поскольку амплитуда сезонных колебаний немного изменяется со временем, можно предположить существование мультипликативной модели. Определим её компоненты.
Шаг 1. Проведём выравнивание исходных уровней ряда методом скользящей средней (по аналогии с методикой выравнивания при построении аддитивной модели). Результаты расчётов оценок сезонной компоненты представлены в табл. 5.10.
Шаг 2. Найдём оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр.6 табл. 5.10).
Используем эти оценки для расчета значений сезонной компоненты (табл. 5.11). Для этого найдём средние за каждый квартал оценки сезонной компоненты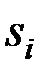 
.
Таблица 5.10
Расчёт оценок сезонной компоненты в мультипликативной модели
№
квартала,
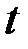
| Потребление
электро–энергии,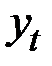 
| Итого за четыре квартала | Скользящая средняя по кварталам | Центриро–ванная скользящая средняя | Оценка сезонной компоненты |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | 30 22 25 45 36 24 30 50 48 28 32 55 45 33 35 54 42 30 | 122 128 130 135 140 152 156 158 163 160 165 168 167 164 161 | 30,50 32,00 32,50 33,75 35,00 38,00 39,00 39,50 40,75 40,00 41,25 42,00 41,75 41,00 40,25 | 31,250 32,250 33,125 34,375 36,500 38,500 39,250 40,125 40,375 40,325 41,625 41,875 41,375 40,625 | 0,800 1,395 1,087 0,698 0,822 1,299 1,223 0,698 0,793 1,354 1,081 0,788 0,846 1,329 |
Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле.
В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала). Имеем:
.
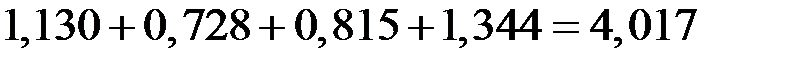Определим корректирующий коэффициент
.
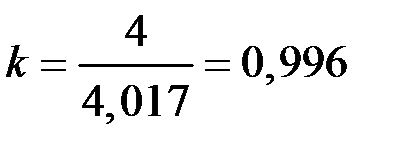Определим скорректированные значения сезонной компоненты, умножив её средние оценки на корректирующий коэффициент k:
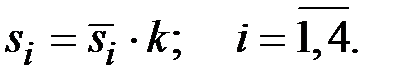
Таблица 5.11
Расчёт сезонной компоненты в мультипликативной модели
|
Показатели | № квартала, i | |||
| I | II | III | IV | |
| Сезонная компонента 1–го года Сезонная компонента 2–го года Сезонная компонента 3–го года Сезонная компонента 4–го года | 1,087 1,223 1,081 | 0,698 0,698 0,788 | 0,800 0,822 0,793 0,846 | 1,395 1,299 1,354 1,329 |
| Итого за i–й квартал (за все годы) | 3,391 | 2,184 | 3,260 | 5,377 |
Средняя оценка сезонной
компоненты для i–го квартала,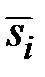 
| 1,130 | 0,728 | 0,815 | 1,344 |
Скорректированная сезонная
компонента,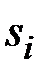 
| 1,125 | 0,725 | 0,812 | 1,338 |
Проверим условие равенства суммы значений сезонной компоненты 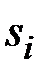числу 4:
.
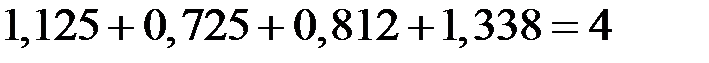Получим следующие значения сезонной компоненты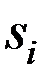 
:
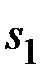= 1,125; 
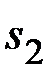= 0,725; 
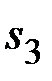= 0,812; 
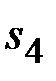= 1,338.
Занесём полученные значения в табл. 5.12 для соответствующих кварталов каждого года (гр.3).
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты.
Получим величины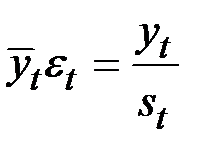 
(гр.4 табл. 5.12), которые содержат только тенденцию и случайную компоненту.
Шаг 4. Определим параметры линейного тренда, используя уровни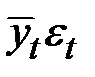 
. Результаты аналитического выравнивания этого ряда дают уравнение тренда в виде:
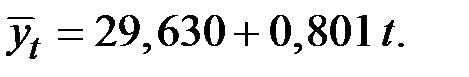
Подставляя в это уравнение значения t = 1, ..., 18, найдём уровни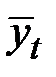 
для каждого момента времени (гр.5 табл. 5.12).
Шаг 5. Найдём уровни ряда по мультипликативной модели, умножив уровни 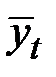на значения сезонной компоненты для соответствующих кварталов (гр.6 табл. 5.12).
Шаг 6. Расчёт ошибки в мультипликативной модели производится по формуле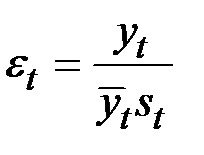 
(гр.7 табл. 5.8).
Таблица 5.12
Расчёт тренда и ошибок в мультипликативной модели
| t |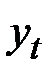 
| 
|
|
| 
|
| 
| 
|
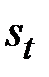
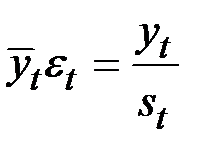
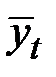
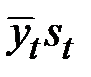
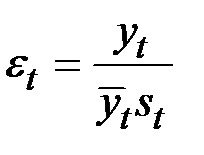
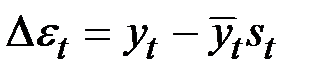
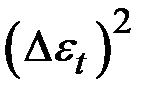
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 30 | 1,125 | 26,667 | 30,431 | 34,235 | 0,876 | –4,235 | 15,934 |
| 2 | 22 | 0,725 | 30,345 | 31,232 | 22,643 | 0,972 | –0,643 | 0,414 |
| 3 | 25 | 0,812 | 30,788 | 32,033 | 26,011 | 0,961 | –1,011 | 1,022 |
| 4 | 45 | 1,338 | 33,632 | 32,834 | 43,932 | 1,024 | 1,068 | 1,141 |
| 5 | 36 | 1,125 | 32,000 | 33,635 | 35,839 | 0,951 | –1,839 | 3,383 |
| 6 | 24 | 0,725 | 33,103 | 34,436 | 24,966 | 0,961 | –0,966 | 0,933 |
| 7 | 30 | 0,812 | 36,946 | 35,237 | 28,612 | 1,048 | 1,388 | 1,925 |
| 8 | 50 | 1,338 | 35,369 | 36,038 | 48,219 | 1,037 | 1,781 | 3,173 |
| 9 | 48 | 1,125 | 42,667 | 36,839 | 41,444 | 1,158 | 6,556 | 42,983 |
| 10 | 28 | 0,725 | 38,621 | 35,640 | 25,289 | 1,026 | 0,711 | 0,506 |
| 11 | 32 | 0,812 | 39,409 | 38,441 | 31,214 | 1,025 | 0,786 | 0,618 |
| 12 | 55 | 1,338 | 41,106 | 39,242 | 52,506 | 1,048 | 2,494 | 6,221 |
| 13 | 45 | 1,125 | 40,000 | 40,043 | 45,048 | 0,999 | –0,048 | 0,002 |
| 14 | 33 | 0,725 | 45,517 | 40,844 | 29,612 | 1,114 | 3,388 | 11,479 |
| 15 | 35 | 0,812 | 43,103 | 41,645 | 33,816 | 1,035 | 1,184 | 1,402 |
| 16 | 54 | 1,338 | 40,359 | 42,446 | 56,793 | 0,951 | –2,793 | 5,799 |
| 17 | 42 | 1,125 | 35,333 | 43,247 | 48,653 | 0,863 | –6,653 | 44,261 |
| 18 | 30 | 0,725 | 41,379 | 44,048 | 31,935 | 0,939 | –1,935 | 3,743 |
Если ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного для изучения его взаимосвязи с другими рядами.
Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как
.
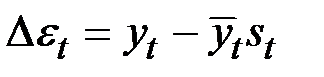В данной модели сумма квадратов абсолютных ошибок составляет 148,940. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна
.
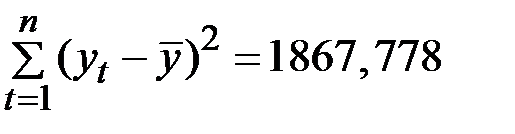Коэффициент детерминации модели равен
.
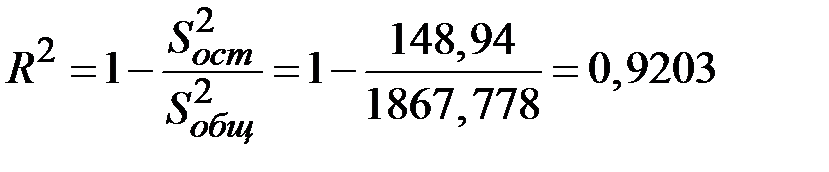Доля объяснённой дисперсии уровней ряда равна 0,9203 или 92,03%.
Выявление и устранение сезонного эффекта («десезонализация уровней ряда») используются в двух направлениях.
1. Воздействие сезонных колебаний следует устранять на этапе предварительной обработки исходных данных при изучении взаимосвязи нескольких рядов. Поэтому в российских и международных статистических сборниках часто публикуются данные, в которых устранено влияние сезонной компоненты (если это помесячная или поквартальная статистика), например, показатели объёмов производства в отдельных отраслях промышленности, уровня безработицы и т.д.
2. Сезонный эффект используется в прогнозировании уровней ряда в будущие моменты времени.
Шаг 7. Спрогнозируем потребление электроэнергии на ближайшие полгода по мультипликативной модели.
Прогнозное значение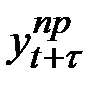 
уровня ряда в мультипликативной модели есть произведение трендовой и сезонной составляющих.
Для определения трендовой компоненты за каждый квартал воспользуемся уравнением тренда
.
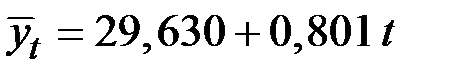Получим
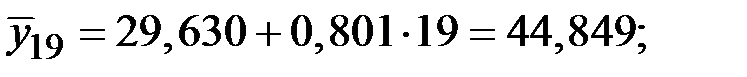
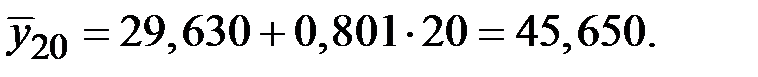
Значения сезонной компоненты равны
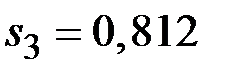(IΙΙ квартал); 
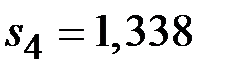(IV квартал).
Таким образом,
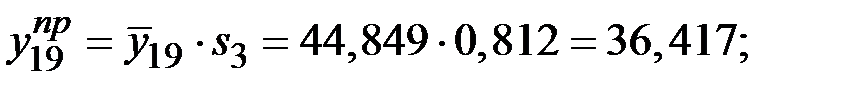
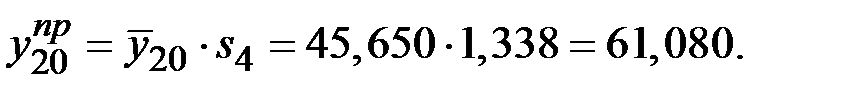
Прогноз объёма потребления электроэнергии на второе полугодие последнего года составит
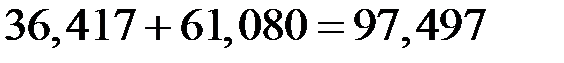млн. кВт·ч.
3. Можно строить модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. Например, при моделировании поквартальных данных модель должна включать 4 независимые переменные – фактор времени и три фиктивные переменные.
Каждая фиктивная переменная отражает сезонную (циклическую) компоненту ряда для какого−либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.
Пусть имеется временной ряд, содержащий циклические колебания периодичностью L . Модель регрессии с фиктивными переменными для этого ряда будет иметь вид:
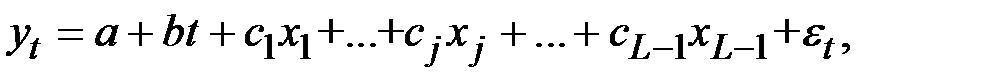
где 
Например, при моделировании сезонных колебаний на основе поквартальных данных за несколько лет число кварталов внутри одного года L = 4, а общий вид модели следующий:
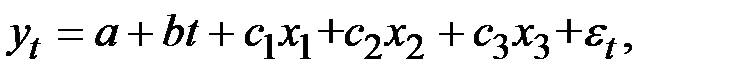
где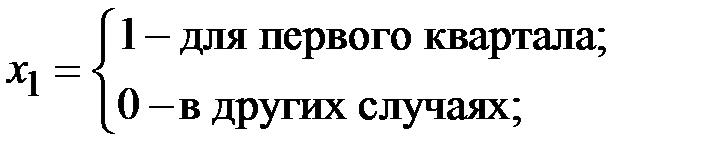 
Уравнения трендов для кварталов будет иметь следующий вид:
для 1−го квартала: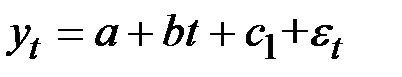 
;
для 2−го квартала: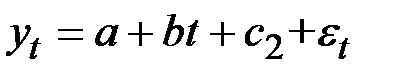 
;
для 3−го квартала: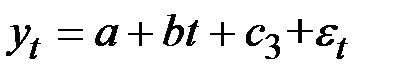 
.
Фиктивные переменные позволяют дифференцировать величину свободного члена уравнения регрессии для каждого квартала. Она составит для I кв.: (a + с1); для II кв.: (а + с2); для III кв.: (a + c3); для IV кв.: а.
Параметр b в этой модели характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции.
Рассмотренная модель есть аналог аддитивной модели ряда, поскольку фактический уровень ряда есть сумма трендовой, сезонной и случайной составляющих.
Основной недостаток модели с фиктивными переменными для описания сезонных и циклических колебаний – наличие большого количества переменных.
Применительно к нашей задаче о потреблении электроэнергии в модели будут четыре независимые переменные: t, x1, x2, x3 и результативная переменная у t . Составим матрицу исходных данных (табл. 5.13).
Обычным МНК оценим параметры уравнения регрессии
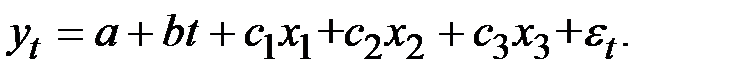
Результаты оценки уравнения регрессии приведены в табл. 5.14.
Уравнение регрессии имеет вид:
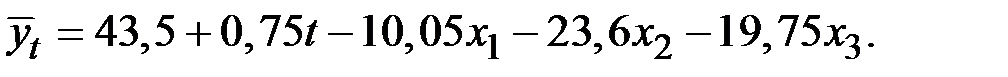
Коэффициент детерминациии этого уравнения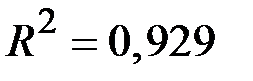 
.
Проанализируем полученные результаты.
Влияние сезонной компоненты в каждом квартале статистически значимо (фактические значения Т−критерия по модулю больше 2 для параметров при переменных x1, x2, x3 и константы а).
Параметр а = 43,5 есть сумма начального уровня ряда и сезонной компоненты в IV квартале.
Сезонные колебания в I, II и III кварталах приводят к снижению этой величины, о чем свидетельствуют отрицательные оценки параметров при переменных x1, x2 и x3.
Отметим, что эти параметры не равны значениям сезонной компоненты, поскольку они характеризуют не сезонные изменения уровней ряда, а их отклонения от уровней, учитывающих сезонные воздействия в IV квартале.
Положительная величина параметра b = 0,75 при переменной времени свидетельствует о наличии возрастающей тенденции в уровнях ряда.
Его абсолютное значение говорит о том, что средний за квартал абсолютный прирост объёма потребления электроэнергии составляет 0,75 млн. кВт·ч.
Так как фактическое значение Т−критерия равно 5,14, можно утверждать, что существование в уровнях ряда тенденции установлено.
Общая сумма квадратов отклонений уровней ряда от общей средней составляет величину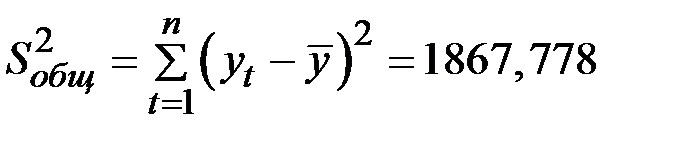 
.
С использованием коэффициента детерминации модели (R2 = 0,929) определим остаточную сумму квадратов уровней ряда
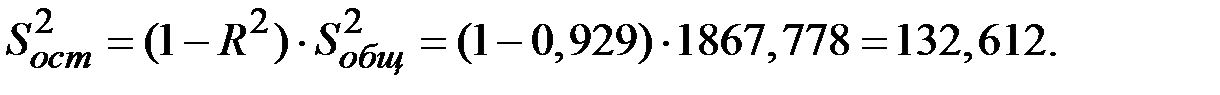
Остаточная сумма квадратов абсолютных ошибок по аддитивной модели была рассчитана ранее (табл. 5.9) и составляет 148,05. Следовательно, модель регрессии с фиктивными переменными описывает динамику ряда потребления электроэнергии лучше, чем аддитивная модель.
Таблица 5.13
Данные для расчёта параметров уравнения регрессии
с фиктивными переменными по ряду потребления электроэнергии
| t | x1 | x2 | x3 | y t |
| 1 | 1 | 0 | 0 | 30 |
| 2 | 0 | 1 | 0 | 22 |
| 3 | 0 | 0 | 1 | 25 |
| 4 | 0 | 0 | 0 | 45 |
| 5 | 1 | 0 | 0 | 36 |
| 6 | 0 | 1 | 0 | 24 |
| 7 | 0 | 0 | 1 | 30 |
| 8 | 0 | 0 | 0 | 50 |
| 9 | 1 | 0 | 0 | 48 |
| 10 | 0 | 1 | 0 | 28 |
| 11 | 0 | 0 | 1 | 32 |
| 12 | 0 | 0 | 0 | 55 |
| 13 | 1 | 0 | 0 | 45 |
| 14 | 0 | 1 | 0 | 33 |
| 15 | 0 | 0 | 1 | 35 |
| 16 | 0 | 0 | 0 | 54 |
| 17 | 1 | 0 | 0 | 42 |
| 18 | 0 | 1 | 0 | 30 |
Таблица 5.14
Уравнение регрессии с фиктивными переменными
| Переменная | Коэффициент | Стандартная ошибка | Т−критерий |
| Константа | 43,50 | 2,17 | 20,09 |
| t | 0,75 | 0,15 | 5,14 |
| x1 | −10,05 | 2,15 | −4,67 |
| x2 | −23,60 | 2,15 | −11,00 |
| x3 | −19,75 | 2,27 | −8,71 |
Выполним прогнозирование по полученной модели
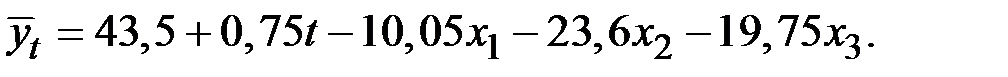
Потребление электроэнергии за третий квартал последнего года:
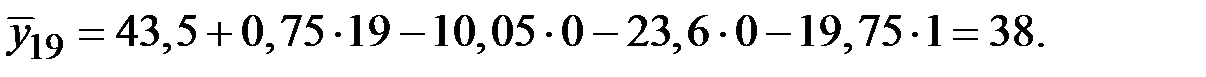
Потребление электроэнергии за четвёртый квартал последнего года:
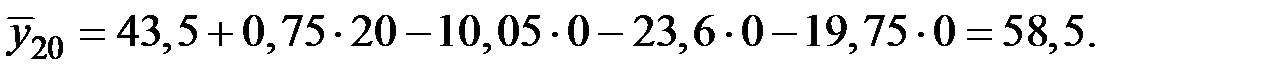
Потребление электроэнергии за ближайшие полгода:
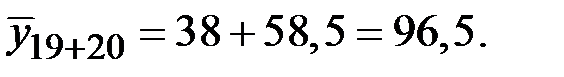
Дата: 2019-03-05, просмотров: 809.
