Понятие эластичности функции нескольких переменных вводится аналогично понятию эластичности функции одной переменной.

Пусть, например, 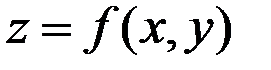 – функция двух переменных.

Её частные приращения:

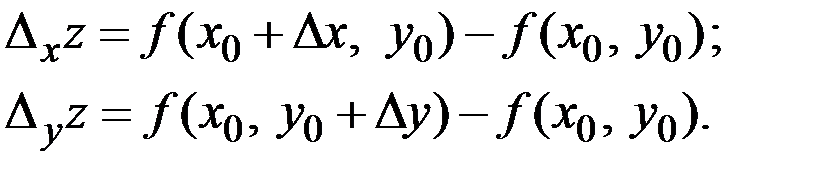
Эластичностью функции 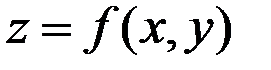 в точке  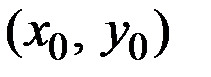пo х называется предел следующего вида

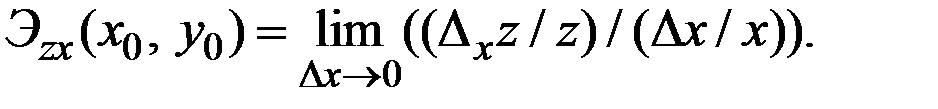
Эластичностью функции 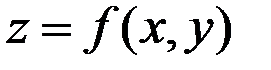 пo у в той же точке называется предел

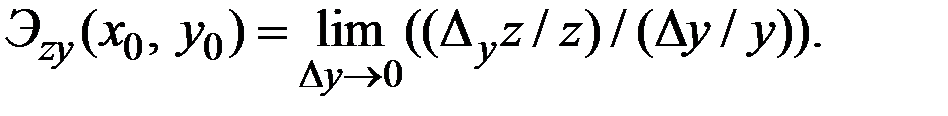
Из определения эластичности вытекают следующие формулы:

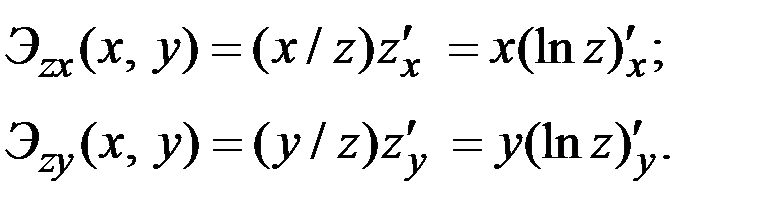
Прим ер 3.12. Найти коэффициенты эластичности по х и по у функции 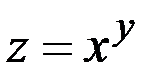 в точке (2; 3).

Решение. Согласно полученным выше формулам имеем

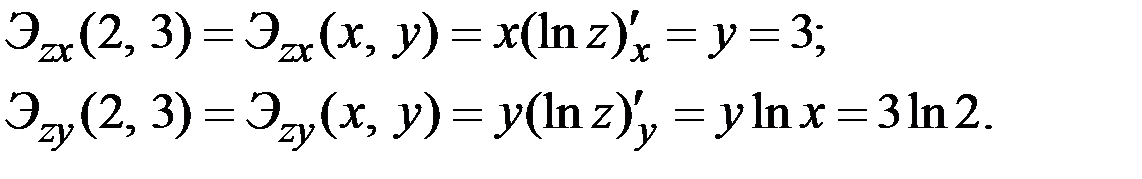
Рассмотренные формулы полностью аналогичны формулам, которые использовались при анализе свойств 1 – 3 эластичности в одномерном случае. Поэтому первые три свойства эластичности справедливы и в случае функции нескольких переменных.

Третье и четвёртое свойства также сохраняются, но формы их записи становятся сложнее.

Остановимся подробнее на этих свойствах.

Свойство 4: Для функций

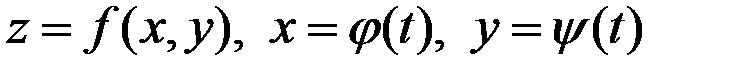
эластичность z пo t в точке 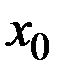, находится по формуле

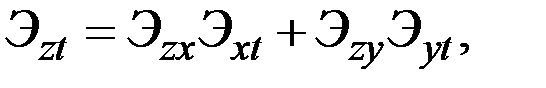
где 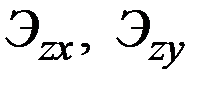 – эластичности z пo х и у в точке ( ,

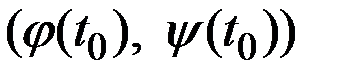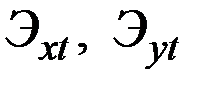 – эластичности х и у по t в точке .

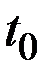Пара функций 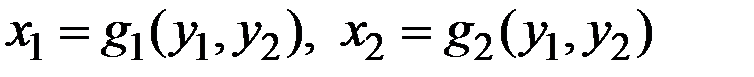, называется обратной для пары функций 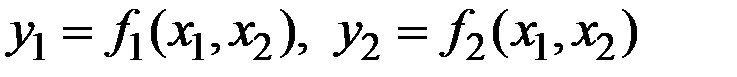, заданных на множестве 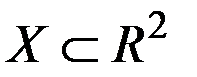, если для любой точки 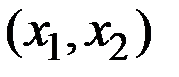из Х выполняются равенства:

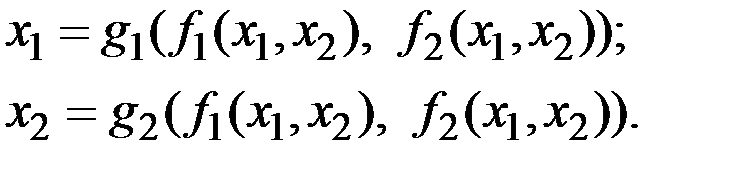
Пример 3.13 . Найти пару обратных функций для функций

,

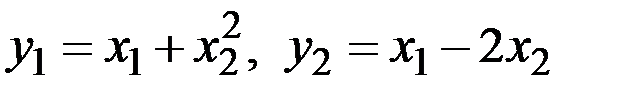заданных в .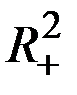

Решение. Из равенства 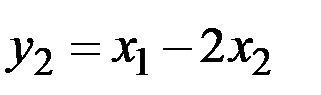 следует, что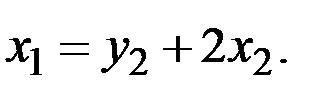  

Поэтому

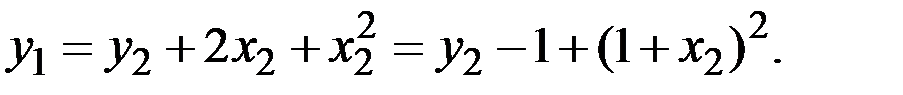
Находим

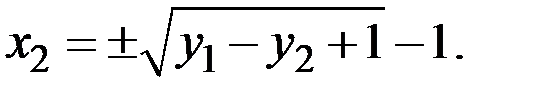
Учитывая, что 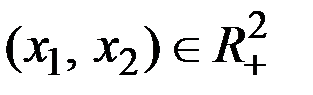 , имеем

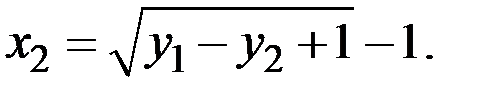
Следовательно,

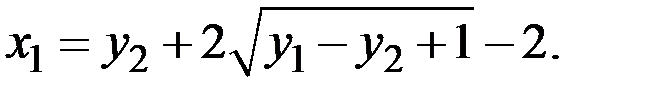
Для любой пары функций 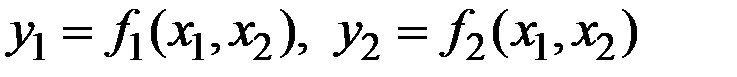 имеем 4 коэффициента эластичности ).

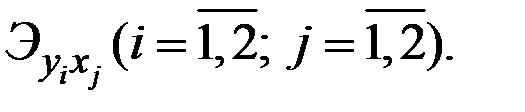Записав их в виде таблицы, получим матрицу размера 2х2:

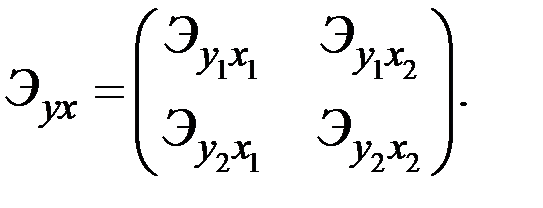
Элементы этой матрицы, расположенные вне главной диагонали, называются перекрёстными коэффициентами эластичности.

Свойство 5. Пусть

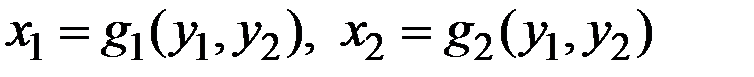
– пара обратных функций для функций

.

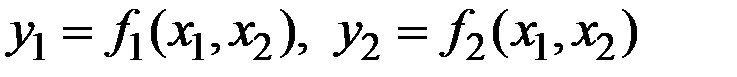Тогда матрица коэффициентов эластичности 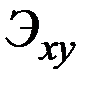 является обратной к матрице .

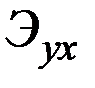Коэффициенты эластичности используются при анализе функций спроса при любом числе различных товаров.

В качестве примера рассмотрим случай с двумя товарами.

Пусть 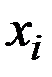 – количество 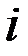–гo товара,

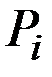 – его цена ( ).

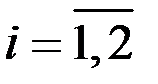Для пары дополняющих товаров (например, чай и сахар) или заменяющих товаров (например, масло и маргарин) естественно считать, что спрос на каждый товар зависит от обеих цен 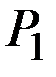 и :

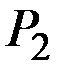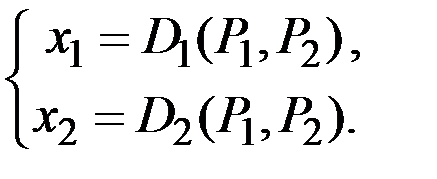
Предположим, что не только цены определяют спрос, но и, напротив, спрос определяет цены.

Иными словами, будем считать, что эту систему можно разрешить относительно 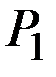 и 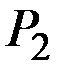 в следующем виде:

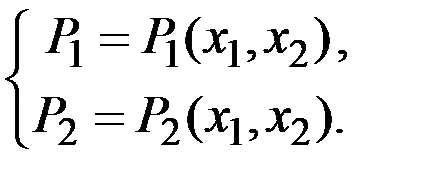
Эти системы определяют две пары взаимно обратных функций.

Согласно свойству 5 матрица коэффициентов эластичности цен по спросу может быть найдена как обратная матрица

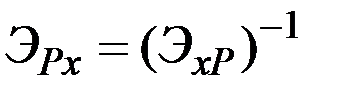
к матрице 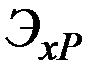 коэффициентов эластичности спроса по ценам.

Заметим, что в случае, когда перекрёстные коэффициенты не равны нулю, то

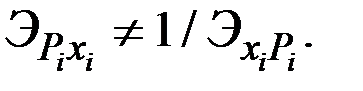
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 3

1. Поясните различие задач экономической статики и динамики.

2. Охарактеризуйте различие содержания решаемых задач, математического аппарата и получаемых результатов для экономических моделей с дискретным и непрерывным временем.

3. Сформулируйте понятие экономического равновесия. Чем устойчивое равновесие отличается от неустойчивого?

4. Как связан темп прироста выпуска с нормой накопления?

5. Поясните особенности использования модели Вальраса.

6. Как выбрать норму накопления при заданном темпе прироста потребления в макромодели роста?

7. В чём состоит проблема выбора наилучшего темпа роста потребления в модели Харрода–Домара?

8. Чем предпосылки модели Солоу отличаются от предпосылок модели Харрода–Домара?

9. Какие общие принципы заложены в моделях Солоу и Харрода–Домара?

Задание 3.1. Дана модель Солоу с производственной функцией 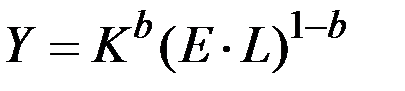, где Y – выпуск, K – капитал,  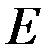– эффективность труда, L – труд,  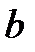– параметр модели. Доля дохода капитала в общем доходе составляет 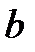, темп прироста численности населения равен n% в год, темп прироста параметра эффективности труда составляет g% в год, а норма амортизации составляет 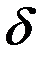% в год (табл. 3.5).

1. Определить норму сбережения, потребление на единицу эффективного труда и капиталовооружённость эффективного труда, соответствующие «золотому правилу».

2. Считаем, что экономика изначально находится на траектории сбалансированного роста, затем норма сбережений изменилась до значения 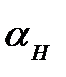%. Определите потребление на единицу эффективного труда до увеличения нормы сбережений, сразу после увеличения нормы сбережений и в долгосрочном периоде.

Таблица 3.5

Исходные данные для анализа модели Солоу

№ вари-анта	Параметр модели	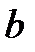Темп прироста численности населения n%	Темп прироста эффективности труда g%	Норма амортизации 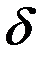%	Новая норма сбережений %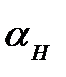
1	0,35	1,5	3,6	4,8	20
2	0,32	1,3	2,8	6,5	34
3	0,36	2,4	2,1	3,4	21
4	0,41	1,6	1,6	2,8	24
5	0,42	2,4	2,8	4,7	34
6	0,26	0,8	2,4	2,9	38
7	0,35	1,3	1,6	4,6	28
8	0,41	1,4	2,8	2,8	34
9	0,36	1,7	2,1	7,1	41
10	0,23	2,4	1,9	4,6	24
11	0,42	1,6	2,8	2,8	34
12	0,26	2,8	2,4	2,7	25
13	0.29	1,5	2,6	4,8	26
14	0,35	1,3	2,8	2,5	34
15	0,41	2,4	2,1	3,4	41
16	0,36	1,6	3,3	2,8	24
17	0,40	2,4	2,8	5,7	34
18	0,42	2,8	2,4	2,9	38
19	0,26	1,3	1,6	5,6	40
20	0,35	1,4	2,8	2,8	34
21	0,46	1,7	2,1	6,1	41
22	0,36	2,4	1,6	4,6	24
23	0,43	1,6	2,8	2,8	34
24	0,42	2,8	2,4	4,7	25
25	0,26	1,5	3,1	4,8	18