Пусть фирма А предлагает свою продукцию к продаже по цене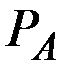 
.
Фирма А называется конкурентной, если существует такая цена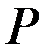 
, что при цене 
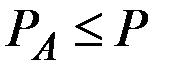фирма может продать любое количество своей продукции, а при цене 
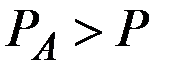не может продать ничего.
Таким образом, спрос на продукцию конкурентной фирмы имеет вид
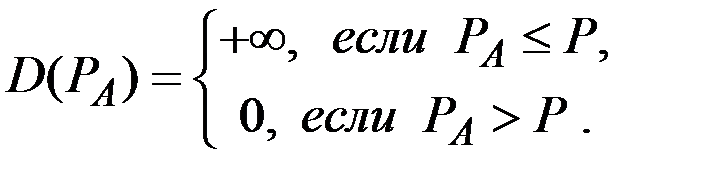
В данном случае кривая спроса является прямой, параллельной оси выпуска О q, а сам спрос является совершенно эластичным (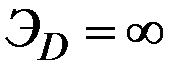 
).
Для того чтобы какая–то реально существующая фирма могла считаться конкурентной, необходимо, чтобы максимальный объём её выпуска составлял лишь незначительную долю от совокупного выпуска её конкурентов.
Для конкурентной фирмы невыгодно продавать продукцию по цене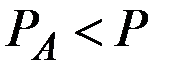 
и невозможно продавать по цене .
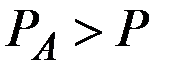Поэтому будем считать, что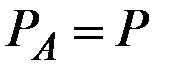 
.
Не имея возможности влиять на цену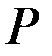 
, конкурентная фирма может увеличивать или уменьшать объём своего выпуска q так, чтобы получить максимальную прибыль 
.
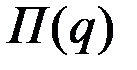Пусть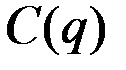 
– издержки, связанные с производством q единиц продукции. Тогда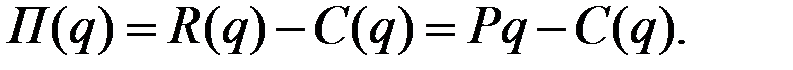 
Пусть функция 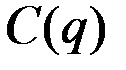определена и дифференцируема на промежутке 
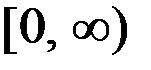. Таким образом, производная 
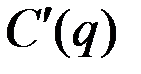определена при 
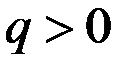и отождествляется с предельными издержками 
.
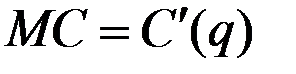Рассмотрим подробнее функции предельных издержек следующих двух типов.
Тип 1. Предельные издержки возрастают на промежутке .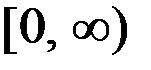
Тип 2. Предельные издержки убывают на отрезке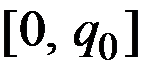 
и возрастают на интервале 
.
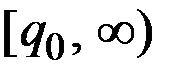В точке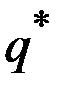 
локального максимума функции прибыли выполняется равенство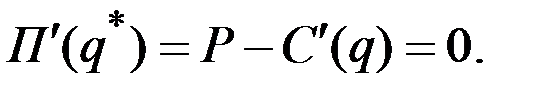 
Отсюда следует, что
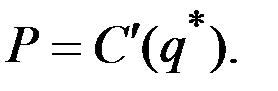
1. Для функции издержек первого типа верно следующее утверждение: если в точке 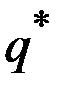предельные издержки совпадают с ценой продукции (выполняется последнее равенство), тo 
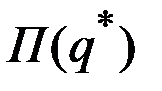– наибольшее значение прибыли на промежутке .
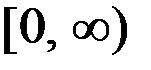Действительно, функция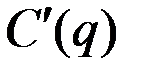 
возрастает на промежутке .
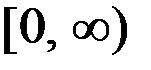Следовательно,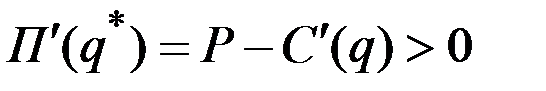 
, когда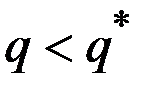 
и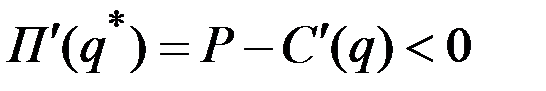 
, когда 
.
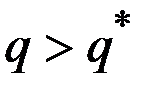Поэтому прибыль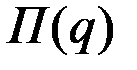 
возрастает на отрезке 
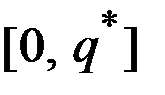и убывает на промежутке 
.
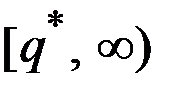Тогда 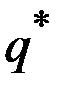– точка глобального максимума функции прибыли.
Как и любая коммерческая фирма, конкурентная фирма стремится максимизировать свою прибыль, поэтому при данной цене продукции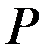 
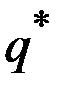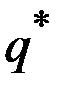она устанавливает объём выпуска равным , где – точка глобального максимума функции прибыли.
Следовательно, последнее равенство влечёт равенство
,
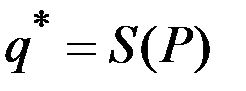где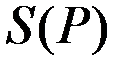 
– функция предложения (т.е. 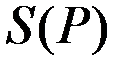– обратная функция для функции ).
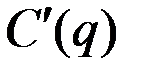С геометрической точки зрения данное утверждение означает, что кривая предложения (график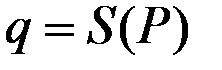 
совпадает с кривой предельных издержек (графиком 
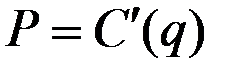) (рис. 4.3).
Рис. 4.3. Определение предложения для функции издержек типа 1
Для функции издержек типа 1 предложение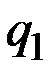 
(при цене 
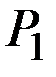) – это проекция на ось Oq точки пересечения прямой 
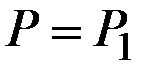, с кривой предельных издержек.
Пример 4 .7. Найти функцию предложения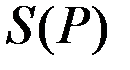 
конкурентной фирмы, если её функция издержек имеет вид
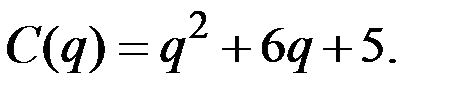
Решение. Находим предельные издержки:
.
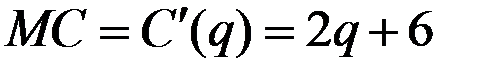Решая уравнение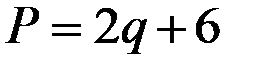 
относительно q, получим функцию предложения конкурентной фирмы
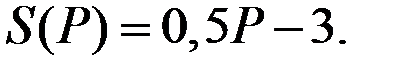
Если в примере цена Р = 10, то предложение
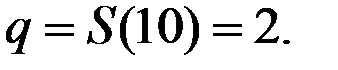
Соответствующие издержки будут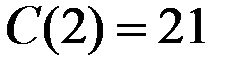 
, прибыль
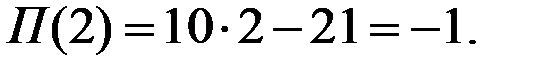
Зачем же фирма решила выпускать 2 единицы продукции, если при этом она имеет убытки в размере 1 денежной единицы?
Не лучше ли было прекратить выпуск?
Ответ на эти вопросы состоит в том, что при выпуске q = 2 фирма несёт минимальные убытки.
Если, например, она прекратит выпуск продукции (q = 0), то убытки составят
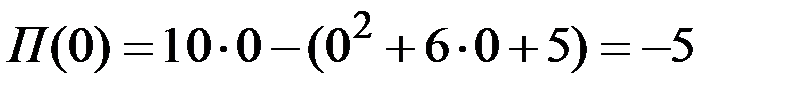денежных единиц.
Очевидно, что убыточное производство возможно только на коротком интервале времени, поэтому найденная функция предложения является функцией предложения в краткосрочном периоде.
2. Изучим функцию предложения конкурентной фирмы в случае функции издержек второго типа.
Пусть 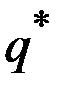– точка глобального максимума функции прибыли 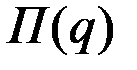на промежутке .
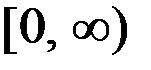Если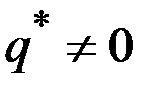 
, то глобальный максимум будет также и локальным.
Поэтому для точки 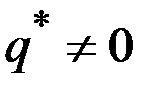выполняется равенство
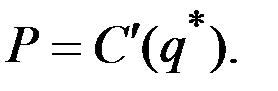
Следовательно, 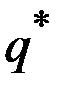– это либо 0, либо решение уравнения
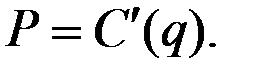
Напомним, что в случае функции издержек второго типа предельные издержки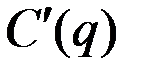 
убывают на отрезке 
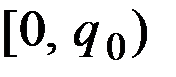и возрастают на интервале 
.
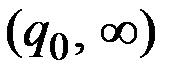Поэтому последнее уравнение P = MC может иметь не более одного решения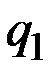 
, на отрезке 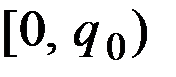и не более одногo решения 
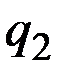, на интервале .
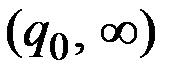Производная прибыли (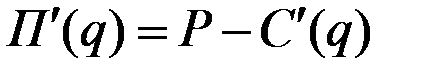 
) меньше нуля на интервале 
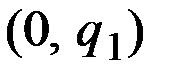и больше нуля на интервале 
.
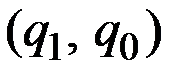Поэтому прибыль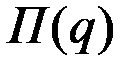 
убывает на интервале 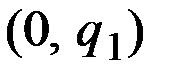и возрастает на интервале 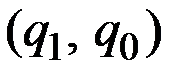(рис. 4.4).
Следовательно, точка 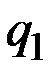, не может быть точкой максимума прибыли. Максимум прибыли (если он существуете) достигается либо в нуле, либо в точке .
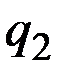Рис. 4.4. Определение предложения для функции издержек типа 2
Пусть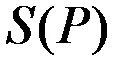 
– функция предложения конкурентной фирмы.
Так как 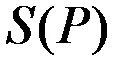– точка глобального максимума функции прибыли 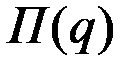, то либо 
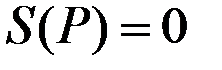, либо 
.
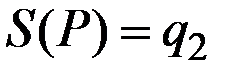Для того чтобы сделать выбор между точками 0 и 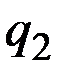, достаточно сравнить значения прибыли в этих точках.
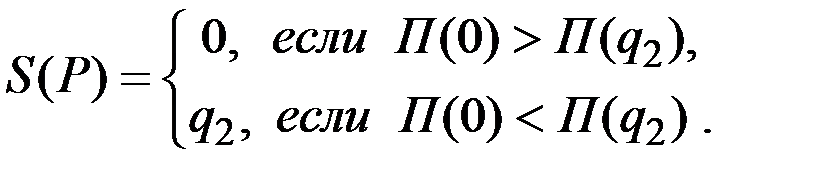
Рассмотрим неравенство
.
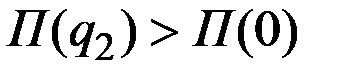Имеем
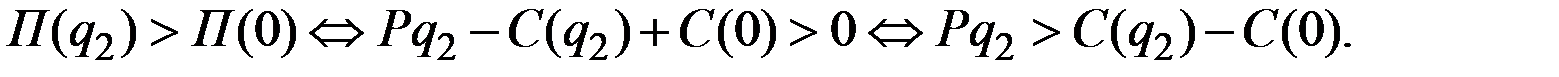
Пусть:
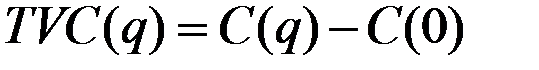
(переменные издержки, связанные с производством q единиц продукции);
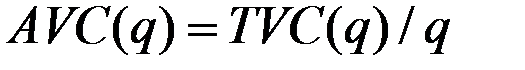
(средние переменные издержки).
Тогда
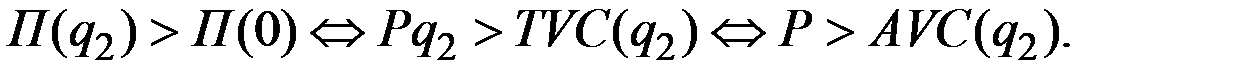
В итоге получаем следующий вид функции предложения для функции издержек второго типа:
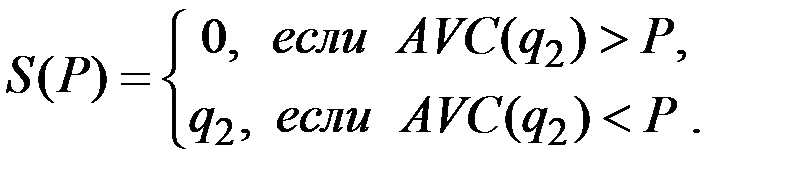
где 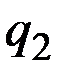– единственное решение уравнения 
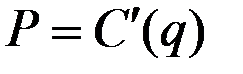на интервале .
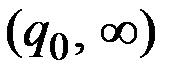С геометрической точки зрения эта формула означает, что кривая предложения совпадает с участком кривой предельных издержек, расположенном выше кривой средних переменных издержек.
Кривая предельных издержек пересекает кривую средних переменных издержек в точке её минимума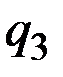 
, (рис. 4.5).
Это не случайно, так как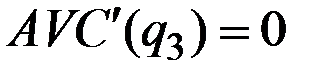 
, каждая такая точка является точкой пересечения кривых 
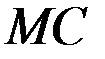и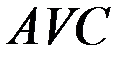 
.
Действительно,
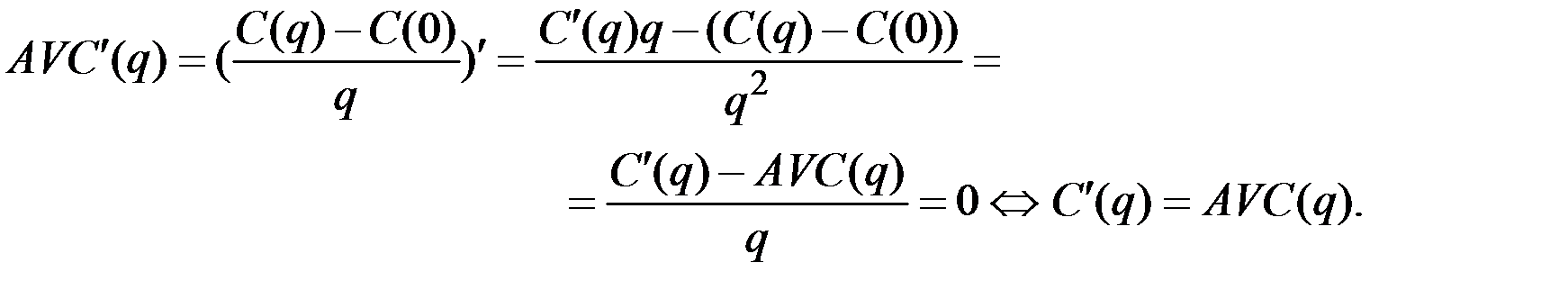
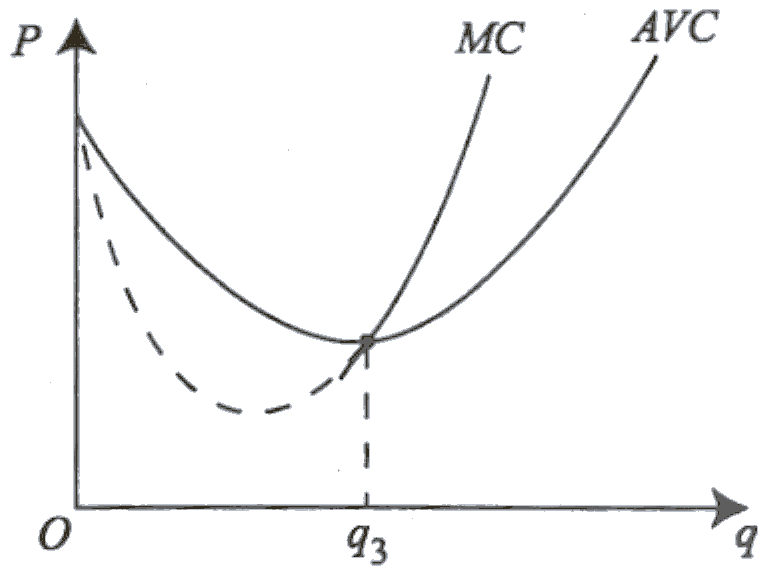
Рис. 4.5. Определение предложения по кривым 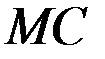и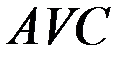
Приме р 4.8 . Найти функцию предложения конкурентной фирмы, если издержки задаются функцией
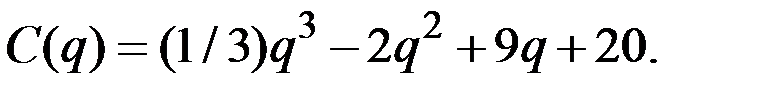
Решение.
Вычисляем предельные издержки
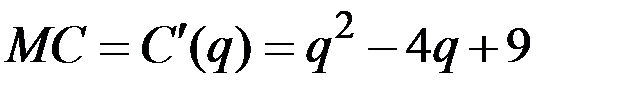
и средние переменные издержки
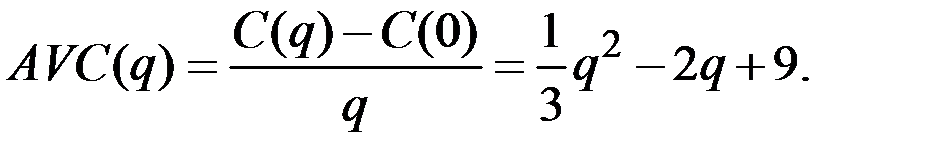
Решая уравнение
,
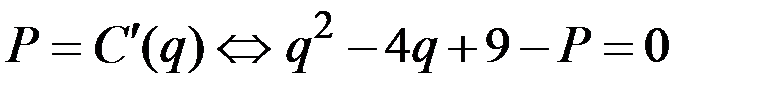находим больший корень
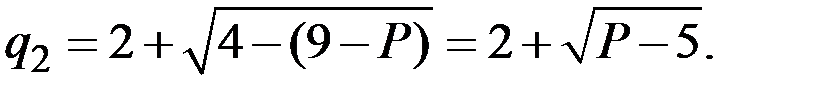
Неравенство
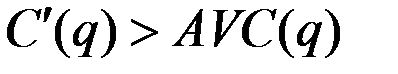
эквивалентно следующим неравенствам:
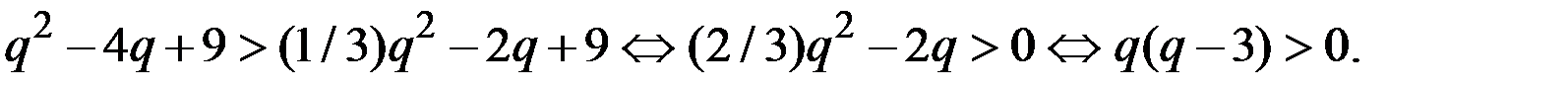
Поэтому кривая 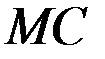расположена выше кривой 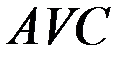на участке справа от точки 
.
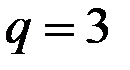В точке 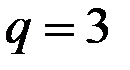предельные издержки равны
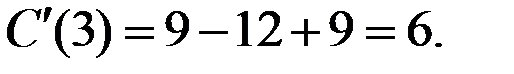
Поэтому функция предложения имеет следующий вид:
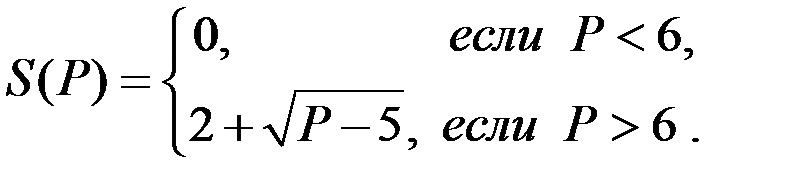
Пример 4.9 . Общие издержки фирмы описываются функцией от объёма выпуска зависимостью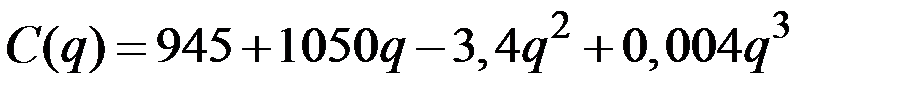 
. Известна функция спроса 
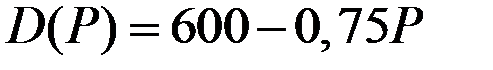. Необходимо:
1. Определить предельные издержки фирмы, их минимальное значение и объём производства при минимальных предельных издержках.
2. Найти функцию предложения этой конкурентной фирмы .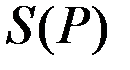
3. Найти оптимальный объём производства и соответствующую цену для фирмы–монополиста при заданной функции спроса.
4. Определить коэффициент превышения оптимальной цены фирмы–монополиста относительно соответствующих издержек.
Решение.
1. Предельные издержки МС составят величину
.
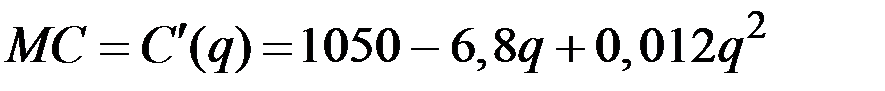Определим точку минимума предельных издержек:
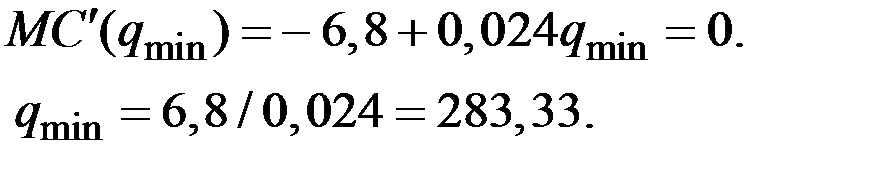
Минимальное значение предельных издержек составит величину
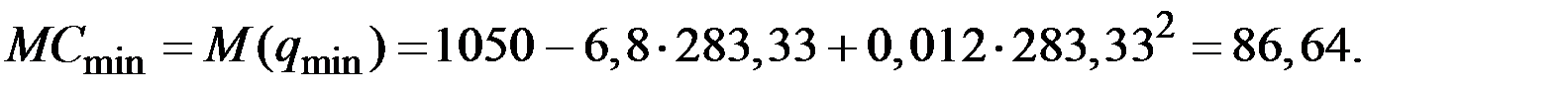
2. Можно найти функцию предложения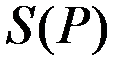 
данной фирмы, вычисляя 
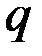для различных цен Р:
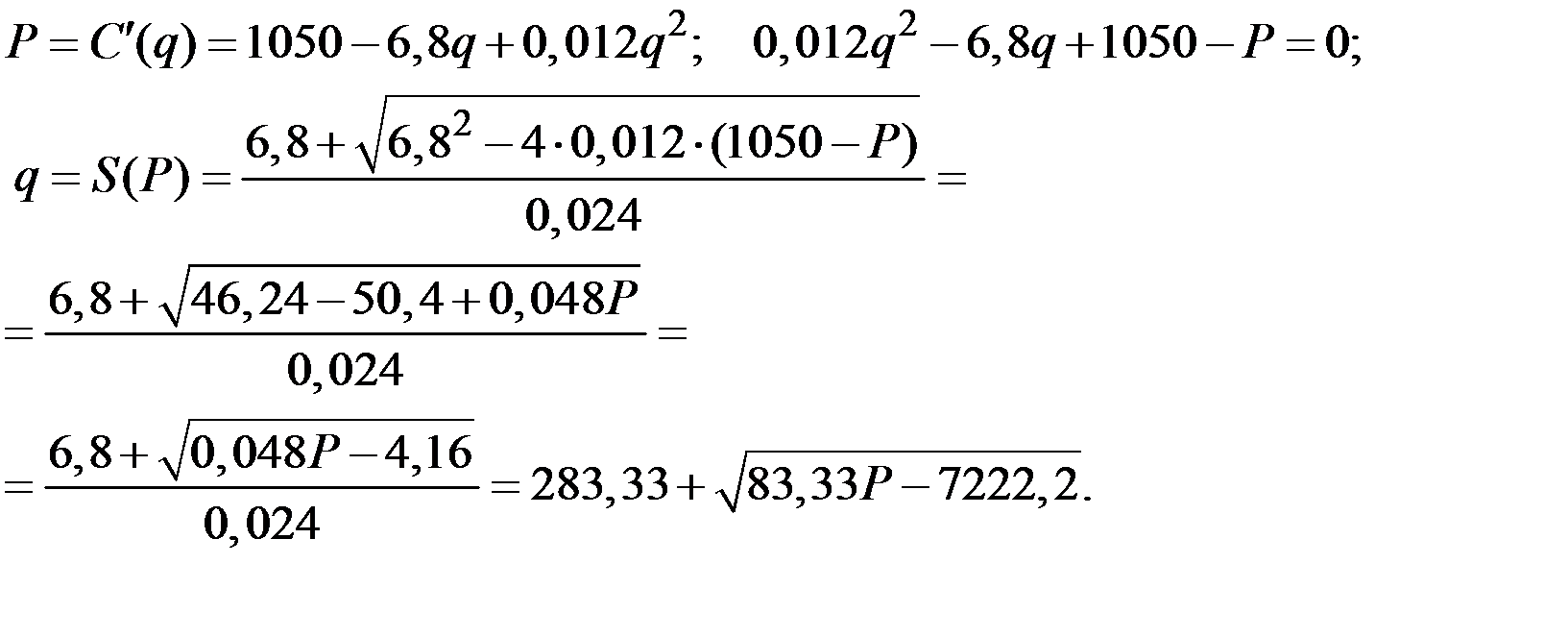
Чтобы подкоренное выражение было положительным, необходимо, чтобы минимальная цена удовлетворяла неравенству
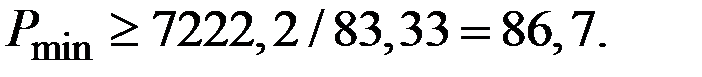
Вид функции предложения для функции издержек второго типа:
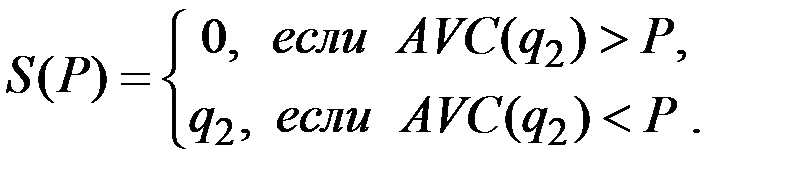
Средние переменные издержки выражаются функцией
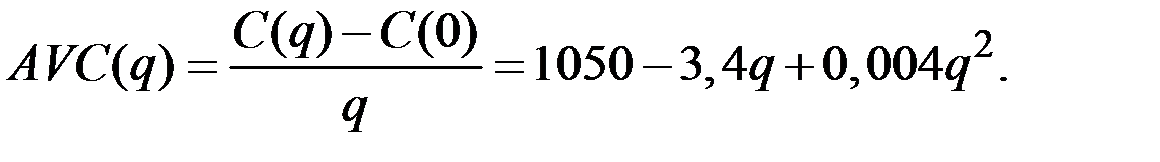
Неравенство 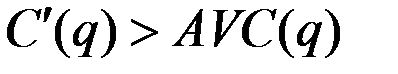эквивалентно соотношениям:
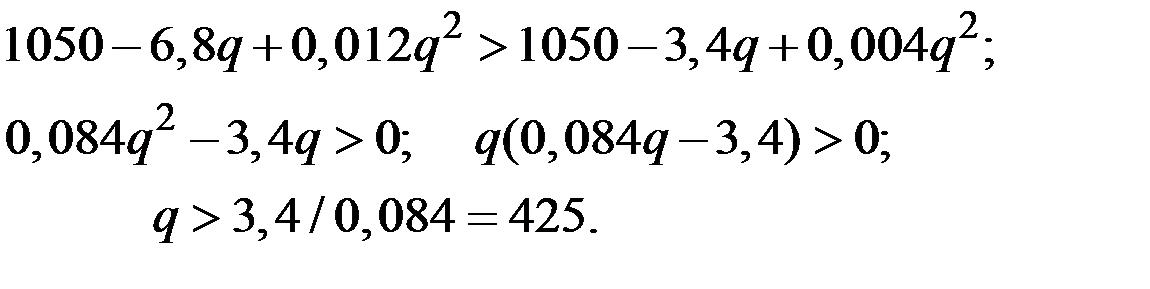
Поэтому кривая 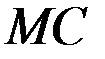расположена выше кривой 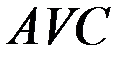на участке справа от точки 
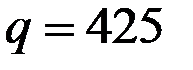. В точке 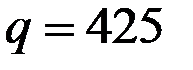предельные издержки равны
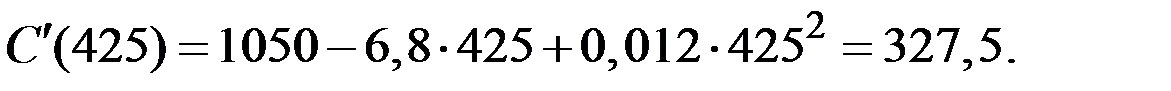
Поэтому функция предложения имеет следующий вид:
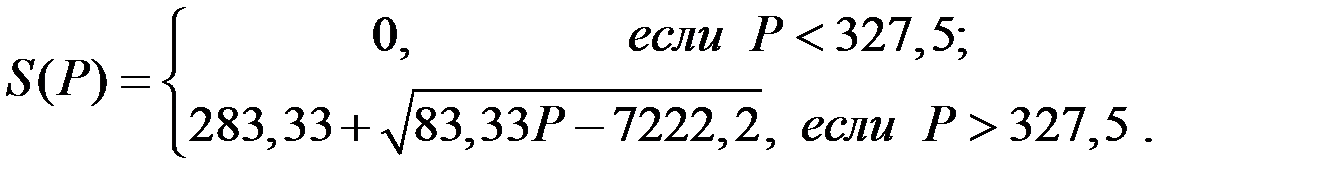
Функция предложения 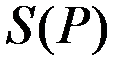и прибыль фирмы для некоторых значений цен имеют следующие значения:
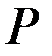
| 86,7 | 100 | 120 | 400 | 425 | 444 | 500 |
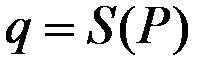
| 283,33 | 316,66 | 336,03 | 444,92 | 451,24 | 455,89 | 468,92 |
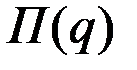
| –90977 | –86907 | –80366 | 31557 | 42385 | 51371 | 77271 |
4. При функции спроса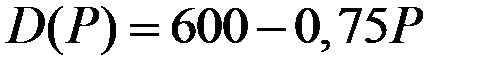 
найдём оптимальный объём производства и соответствующую цену для фирмы–монополиста.
Из функции спроса получаем выражение для цены
.
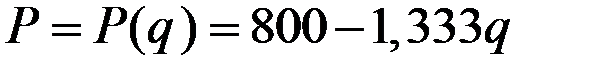Прибыль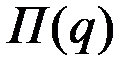 
имеет вид:
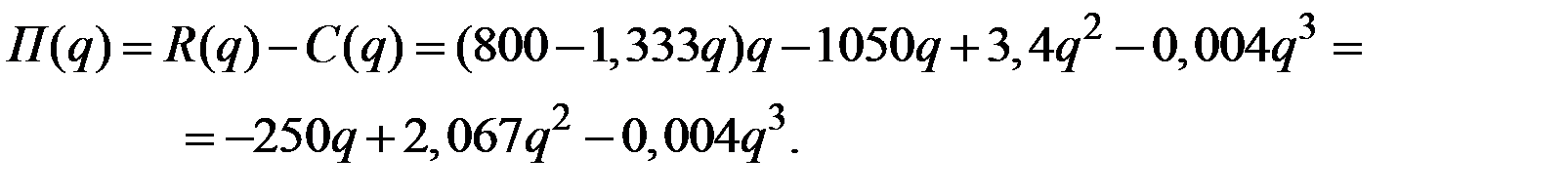
В точке максимума прибыли выполняется равенство
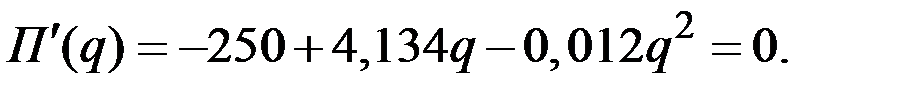
Тогда находим оптимальный объём производства
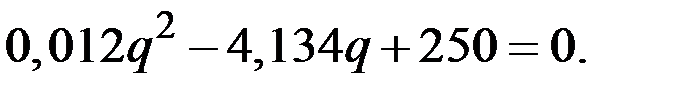
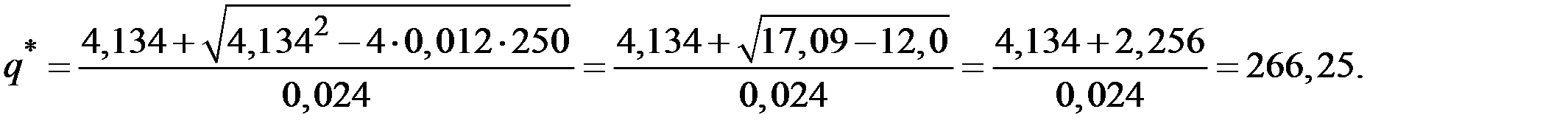
Соответствующая оптимальная цена будет равна величине
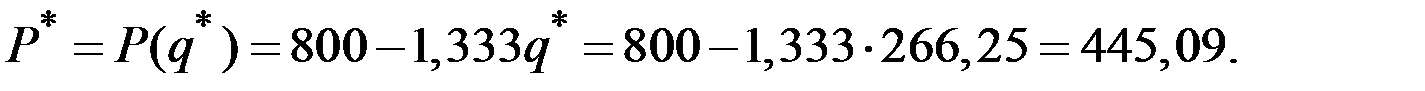
При объёме производства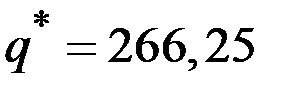 
и цене 
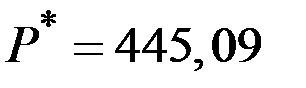прибыль фирмы–монополиста составит значение
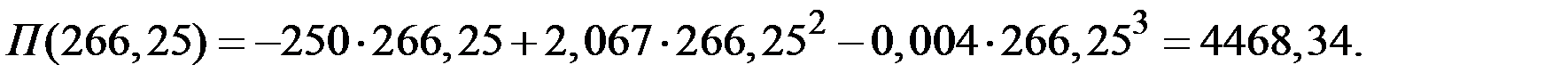
При этом предельные издержки составят величину
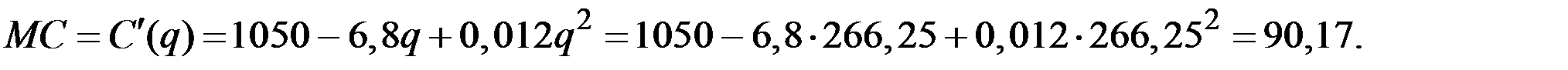
4. Цена, наиболее выгодная для монополии, выше её предельных издержек в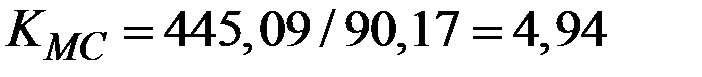 
раза!
Этот же результат можно получить иначе.
Действительно,
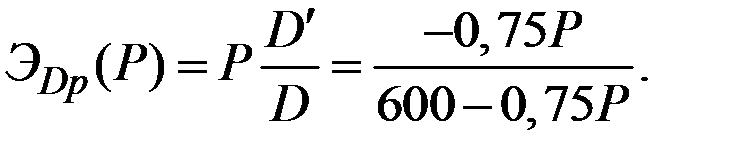
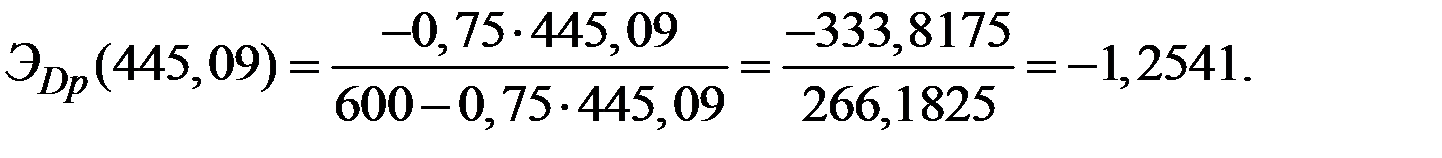
Следовательно, коэффициент увеличения предельных издержек
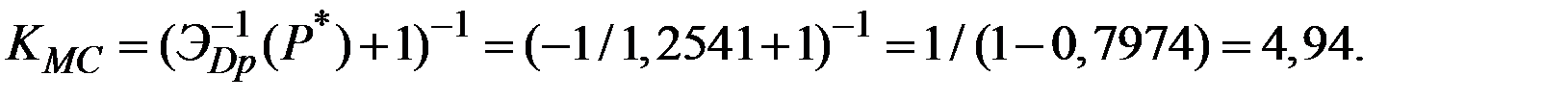
5. При объёме производства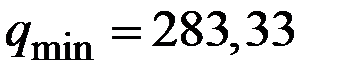 
с минимальными предельными издержками 
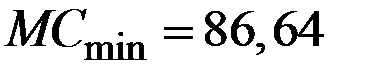цена составит значение
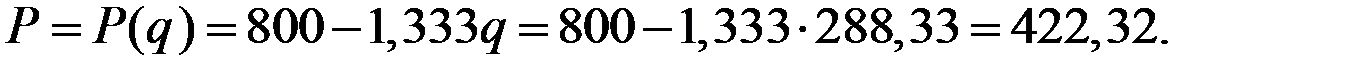
Коэффициент превышения этой цены фирмы–монополиста относительно соответствующих издержек составит значение
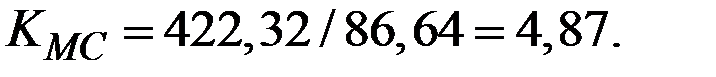
Прибыль фирмы при этом объёме составит
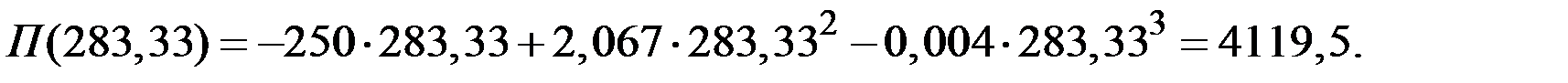
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 4
1. Поясните термин «маржинальные величины».
2. Что такое маржинальный анализ?
3. Поясните основные правила продолжения деятельности фирмы на основе маржинальных величин.
4. Поясните методику использования маржинального анализа.
5. Приведите примеры использования предельных величин в экономике.
Задание 4.1. Фирма производит продукцию и реализует её по цене Р долл. за одну единицу. Постоянные издержки производства составляют TFC долл., а переменные изменяются в зависимости от объёма производства известным образом (табл. 4.5). Требуется проанализировать деятельность фирмы с использованием маржинального анализа. Необходимо:
1. Построить таблицу и графики маржинальных издержек, средних валовых и средних переменных издержек, маржинального дохода.
2. По построенным графикам отыскать оптимальный объём производства.
3. Определить точку банкротства фирмы и предельную точку производства.
4. Проанализировать полученные результаты.
Таблица 4.5
Варианты задания
| № вар. | Цена Р | TFC | Переменные издержки в зависимости от объёма производства | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1 | 72 | 56 | 120 | 165 | 190 | 225 | 290 | 368 | 452 |
| 2 | 84 | 73 | 205 | 304 | 365 | 435 | 564 | 773 | 989 |
| 3 | 61 | 66 | 117 | 145 | 180 | 218 | 270 | 368 | 456 |
| 4 | 36 | 24 | 55 | 84 | 98 | 115 | 184 | 273 | 377 |
| 5 | 70 | 56 | 115 | 162 | 192 | 230 | 291 | 386 | 479 |
| 6 | 79 | 75 | 205 | 305 | 471 | 535 | 664 | 773 | 880 |
| 7 | 61 | 66 | 102 | 145 | 182 | 220 | 290 | 387 | 463 |
| 8 | 70 | 52 | 95 | 148 | 170 | 210 | 275 | 384 | 490 |
| 9 | 69 | 49 | 99 | 136 | 168 | 213 | 278 | 381 | 492 |
| 10 | 77 | 52 | 99 | 140 | 175 | 219 | 285 | 395 | 499 |
| 11 | 71 | 46 | 97 | 136 | 168 | 218 | 278 | 382 | 497 |
| 12 | 80 | 66 | 108 | 140 | 180 | 227 | 279 | 378 | 556 |
| 13 | 95 | 74 | 245 | 314 | 355 | 415 | 504 | 673 | 867 |
| 14 | 70 | 56 | 117 | 162 | 192 | 233 | 290 | 386 | 477 |
| 15 | 80 | 75 | 208 | 305 | 465 | 535 | 664 | 769 | 886 |
| 16 | 61 | 66 | 102 | 149 | 180 | 220 | 290 | 387 | 468 |
| 17 | 70 | 52 | 95 | 143 | 173 | 210 | 275 | 384 | 505 |
| 18 | 59 | 49 | 99 | 136 | 168 | 218 | 279 | 399 | 512 |
| 19 | 72 | 66 | 120 | 165 | 190 | 225 | 290 | 368 | 488 |
| 20 | 84 | 77 | 205 | 309 | 365 | 435 | 564 | 773 | 989 |
| 21 | 81 | 76 | 111 | 145 | 184 | 217 | 275 | 368 | 456 |
| 22 | 95 | 72 | 255 | 314 | 369 | 415 | 504 | 673 | 867 |
| 23 | 68 | 56 | 113 | 164 | 192 | 230 | 293 | 386 | 577 |
| 24 | 80 | 77 | 211 | 305 | 465 | 530 | 656 | 779 | 980 |
| 25 | 78 | 75 | 208 | 309 | 465 | 538 | 666 | 769 | 896 |
Задание 4.2. Общие издержки фирмы описываются функцией от объёма выпуска зависимостью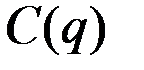 
. Известна функция спроса 
.
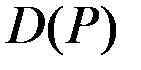Необходимо:
1. Определить предельные издержки фирмы, их минимальное значение и объём производства при минимальных предельных издержках.
2. Найти функцию предложения этой конкурентной фирмы .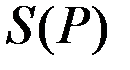
3. Найти оптимальный объём производства конкурентной фирмы при цене товара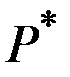 
.
4. Найти оптимальную цену и объём производства продукции при заданной функция спроса для фирмы–монополиста.
Таблица 4.6
Таблица исходных данных
| № | Валовые издержки фирмы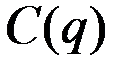 
| Функция спроса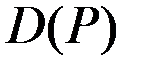 
|
| 1 |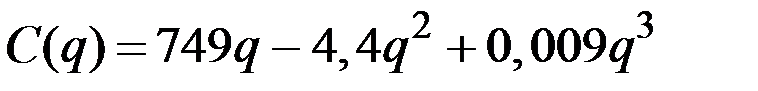 
| 
|
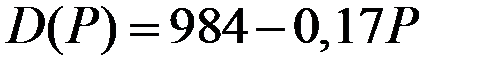
| 2 |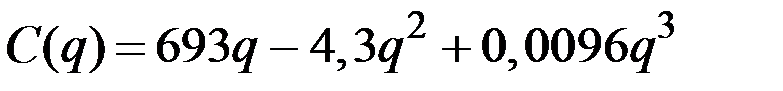 
| 
|
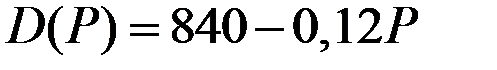
| 3 |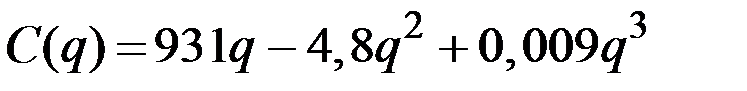 
| 
|
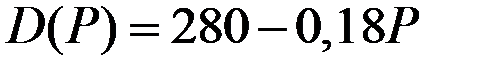
| 4 |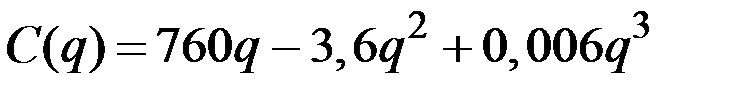 
| 
|
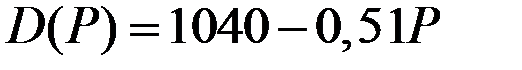
| 5 |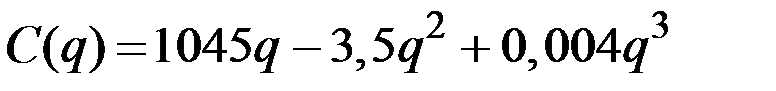 
| 
|
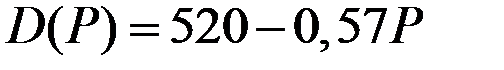
| 6 |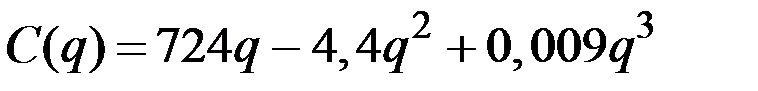 
| 
|
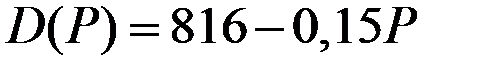
| 7 |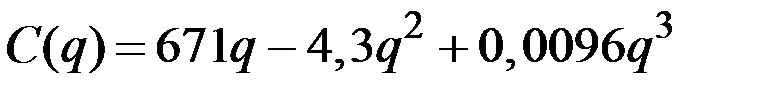 
| 
|
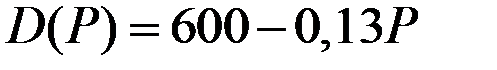
| 8 |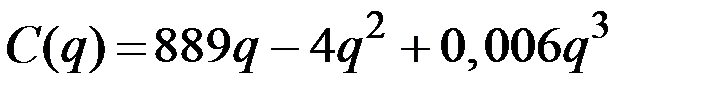 
| 
|
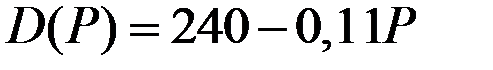
| 9 |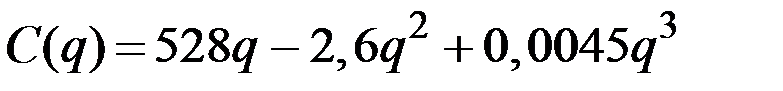 
| 
|
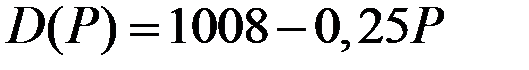
| 10 |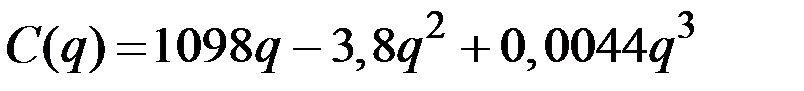 
| 
|
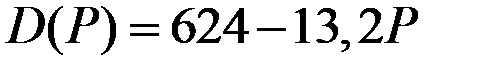
| 11 |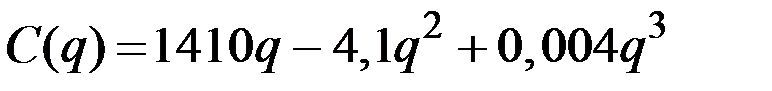 
| 
|
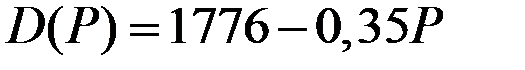
| 12 |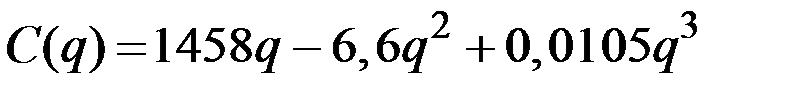 
| 
|
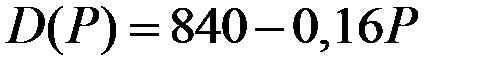
| 13 |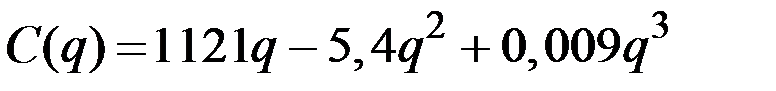 
| 
|
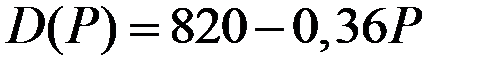
| 14 |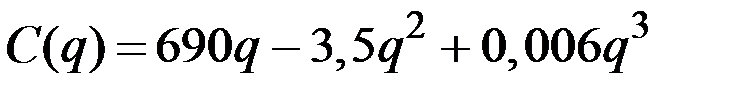 
| 
|
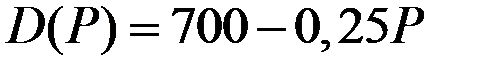
| 15 |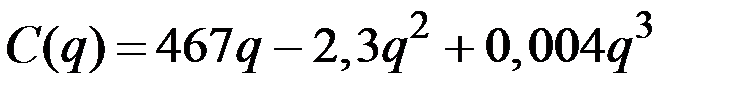 
| 
|
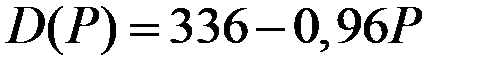
| 16 |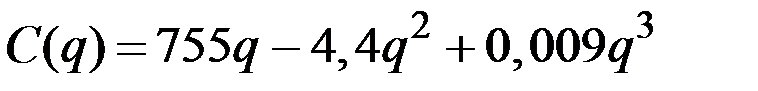 
| 
|
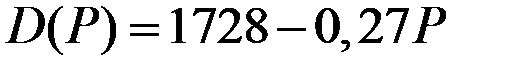
| 17 |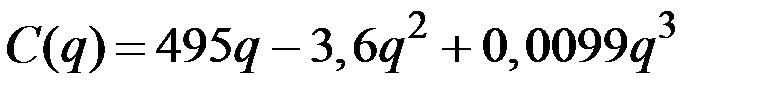 
| 
|
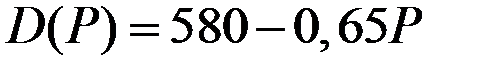
| 18 |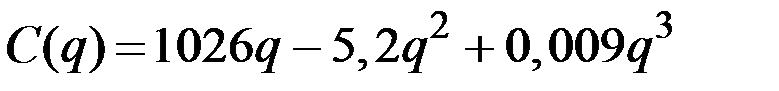 
| 
|
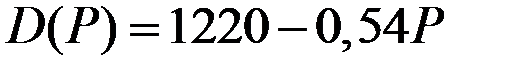
| 19 |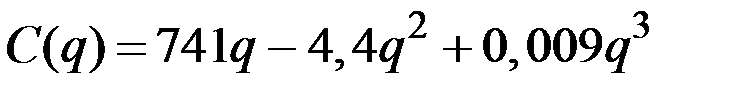 
| 
|
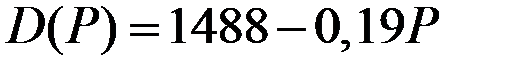
| 20 |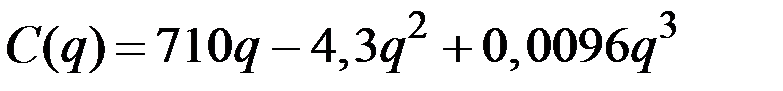 
| 
|
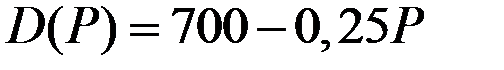
| 21 |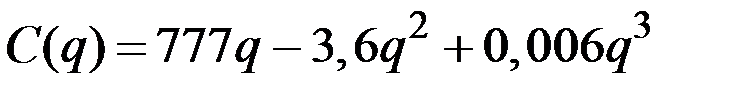 
| 
|
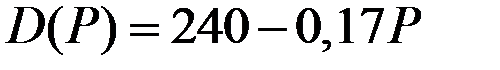
| 22 |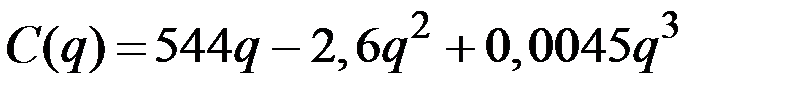 
| 
|
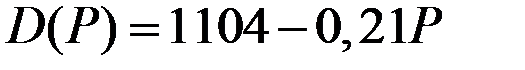
Задание 4.3. В некоторой отрасли действуют 2 фирмы с функциями издержек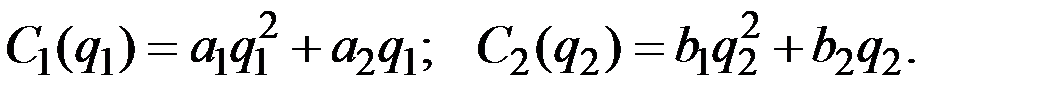 
Спрос на продукцию отрасли задан функцией 
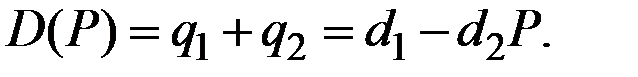В предположении, что фирмы взаимодействуют в соответствии с моделью Курно, определить цену продукции и равновесные объёмы производства для каждой фирмы и всей отрасли.
Исходные данные
| № варианта | Параметры моделей издержек фирм и спроса | |||||
| 
| 
| 
| 
| 
| |
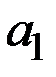
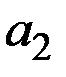
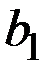
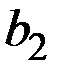
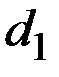
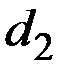
| 1 | 0,7 | 3,3 | 0,8 | 4,1 | 373 | 2,4 |
| 2 | 1,8 | 5,2 | 1,7 | 3,3 | 582 | 3,1 |
| 3 | 1,7 | 1,3 | 1,8 | 5,2 | 2133 | 0,9 |
| 4 | 0,8 | 8,4 | 0,7 | 1,3 | 884 | 5,0 |
| 5 | 3,7 | 3,7 | 1,8 | 8,4 | 307 | 4,7 |
| 6 | 1,8 | 2,8 | 1,7 | 3,7 | 298 | 0,8 |
| 7 | 0,7 | 4,7 | 2,8 | 2,8 | 4227 | 3,7 |
| 8 | 4,8 | 5,0 | 4,7 | 4,7 | 1440 | 2,8 |
| 9 | 1,7 | 3,1 | 5,8 | 5,0 | 321 | 4,7 |
| 10 | 2,8 | 2,8 | 2,7 | 3,1 | 278 | 5,8 |
| 11 | 2,7 | 4,4 | 2,8 | 2,8 | 373 | 1,7 |
| 12 | 5,8 | 2,2 | 4,7 | 4,4 | 582 | 3,8 |
| 13 | 2,7 | 4,7 | 2,8 | 2,2 | 733 | 0,7 |
| 14 | 2,8 | 6,4 | 3,7 | 4,7 | 884 | 5,8 |
| 15 | 0,7 | 5,1 | 0,8 | 6,4 | 307 | 3,3 |
| 16 | 5,8 | 4,9 | 4,7 | 5,1 | 1298 | 5,6 |
| 17 | 3,7 | 5,8 | 3,8 | 4,9 | 4227 | 1,3 |
| 18 | 0,8 | 3,7 | 0,6 | 5,8 | 2240 | 0,4 |
| 19 | 4,7 | 2,8 | 7,8 | 3,7 | 1321 | 3,7 |
| 20 | 5,8 | 4,3 | 4,7 | 2,8 | 473 | 0,8 |
| 21 | 3,7 | 5,8 | 6,5 | 4,3 | 582 | 4,7 |
| 22 | 0,8 | 3,7 | 0,4 | 5,8 | 833 | 5,1 |
| 23 | 4,7 | 6,4 | 5,8 | 3,7 | 774 | 3,0 |
| 24 | 6,5 | 5,1 | 3,7 | 6,4 | 3070 | 1,2 |
| 25 | 1,4 | 3,1 | 1,8 | 5,1 | 2980 | 5,8 |
Дата: 2019-03-05, просмотров: 333.
