Экспоненциальная средняя приводит к смещённым прогнозам, т.е. даёт систематическую ошибку, когда временной ряд имеет тенденцию линейного роста. Для этого случая разработано несколько вариантов адаптивных моделей с использованием экспоненциального сглаживания.
В основе моделей лежит гипотеза о том, что прогноз может быть получен по уравнению
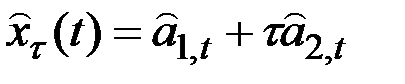 ,
,
где 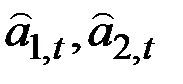 – текущие оценки коэффициентов адаптивного полинома первого порядка.
– текущие оценки коэффициентов адаптивного полинома первого порядка.
1. В двухпараметрической модели Хольта оценка коэффициентов производится следующим образом:
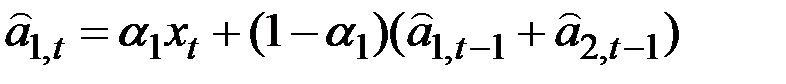 ;
;
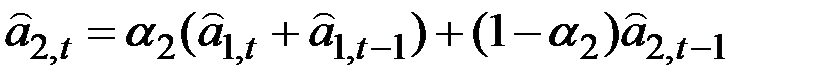 ,
,
где 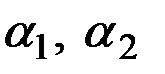 – параметры адаптации экспоненциального сглаживания
– параметры адаптации экспоненциального сглаживания
(0 < 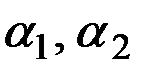 < 1).
< 1).
Эти уравнения могут быть переписаны в виде:
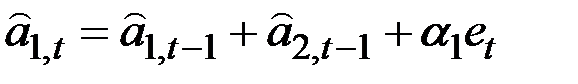 ;
;
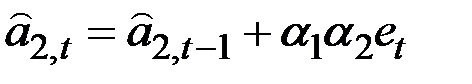 ,
,
где 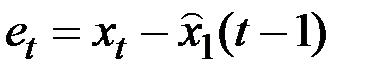 – ошибка прогноза.
– ошибка прогноза.
2. Частный случай модели Хольта: модель Брауна:
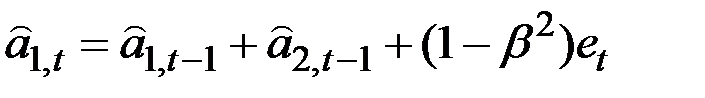 ;
; 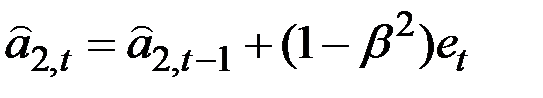 ,
,
где параметр 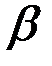 – коэффициент дисконтирования, характеризующий обесценение данных наблюдения за единицу времени, 0 <
– коэффициент дисконтирования, характеризующий обесценение данных наблюдения за единицу времени, 0 < 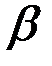 < 1.
< 1.
3. Если модель Хольта усовершенствовать путём включения разности ошибок, то получим трёхпараметрическую модель прогнозирования Дж. Бокса и Г.Дженкинса:
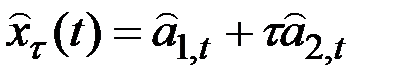 ;
;
 ;
;
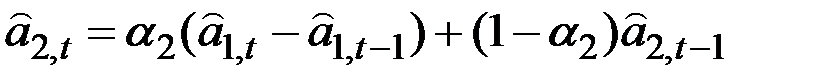 ,
,
где 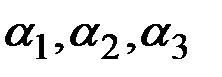 являются параметрами модели, 0 <
являются параметрами модели, 0 < 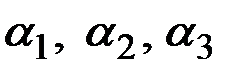 < 1;
< 1;
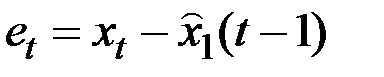 – ошибка прогнозирования.
– ошибка прогнозирования.
На основе практических испытаний модели на многих экономических рядах Бокс и Дженкинс пришли к выводу, что включение в модель разности ошибок не является необходимым. Коэффициент 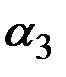 всегда оказывался близким к нулю.
всегда оказывался близким к нулю.
4. Г.Тейл и С.Вейдж вывели выражение для определения оптимальных параметров адаптации, минимизирующих средний квадрат ошибки прогнозирования. Процесс Тейла–Вейджа записываются в виде:
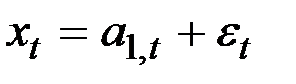 ;
;
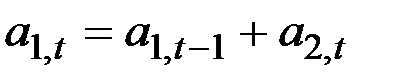 ;
;
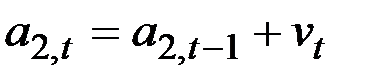 ,
,
где 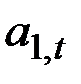 – значение уровня исследуемого ряда
– значение уровня исследуемого ряда 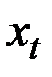 в момент t;
в момент t;
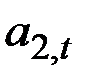 – прирост уровня от момента t – 1 к моменту t;
– прирост уровня от момента t – 1 к моменту t;
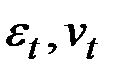 – временные последовательности с нулевым математическим ожиданием, постоянными дисперсиями и отсутствием ковариации, т.е.
– временные последовательности с нулевым математическим ожиданием, постоянными дисперсиями и отсутствием ковариации, т.е.
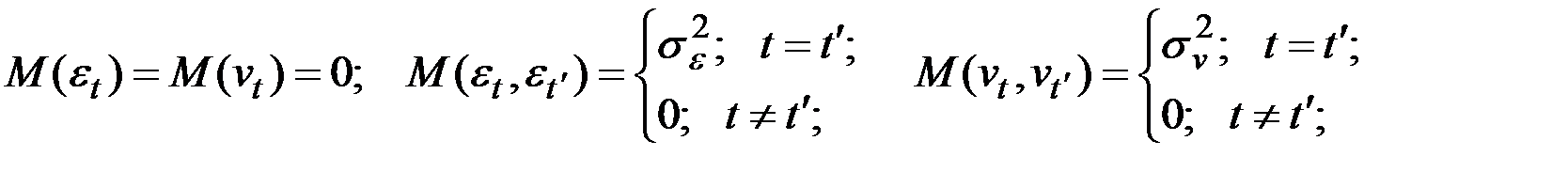
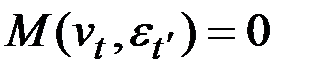 для любой пары
для любой пары 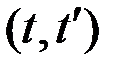 .
.
Схема составления прогноза выглядит следующим образом:
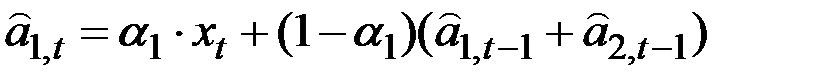 ;
;
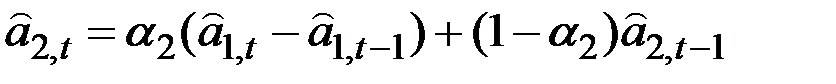 ;
;
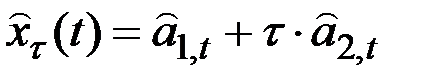 ;
; 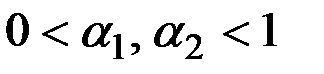 .
.
Если ошибку прогноза, сделанного в момент t на 1 шаг вперёд, обозначить через 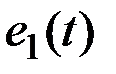 , то уравнения адаптации можно записать в виде:
, то уравнения адаптации можно записать в виде:
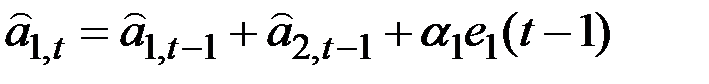 ;
;
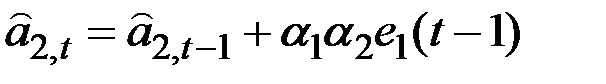 .
.
Ошибка прогноза:
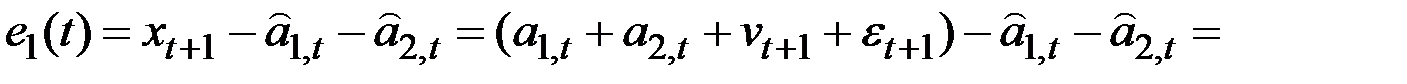
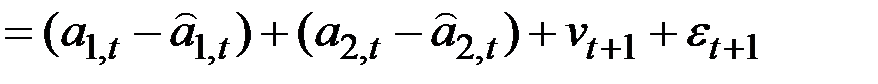 .
.
Ошибка прогноза является суммой трёх компонент: ошибки оценки уровня процесса в момент t, ошибки оценки прироста уровня в момент t и комбинации случайных компонент 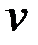 и
и 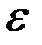 в момент
в момент 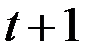 .
.
Несмотря на довольно жёсткую структуру процесса Тейла–Вейджа его можно использовать для аппроксимации некоторых временных рядов.
5. Сезонные модели. В экономике многие явления характеризуются периодически повторяющимися сезонными эффектами. Временные ряды, их отражающие, содержат периодические сезонные колебания. Эти ряды и их колебания можно представить моделями с мультипликативными и с аддитивными коэффициентами сезонности.
Модели с мультипликативными коэффициентами сезонности имеют вид: 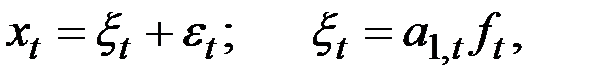
где 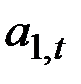 коэффициенты, характеризующие тенденцию развития процесса;
коэффициенты, характеризующие тенденцию развития процесса;
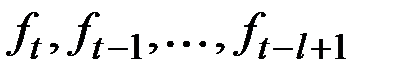 – коэффициенты сезонности;
– коэффициенты сезонности;
 – количество фаз в полном сезонном цикле (если ряд представляет месячные наблюдения, то
– количество фаз в полном сезонном цикле (если ряд представляет месячные наблюдения, то 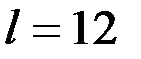 , при квартальных данных
, при квартальных данных 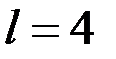 т.п.);
т.п.);
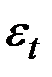 – неавтокоррелированный шум с нулевым мат. ожиданием.
– неавтокоррелированный шум с нулевым мат. ожиданием.
Модели с аддитивными коэффициентами сезонности имеют вид
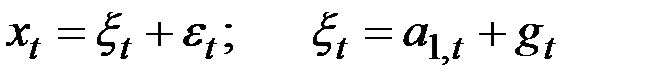 ,
,
где 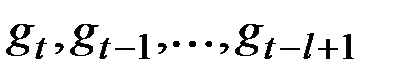 – аддитивные коэффициенты сезонности, а другие параметры аналогичны выше рассмотренным моделям.
– аддитивные коэффициенты сезонности, а другие параметры аналогичны выше рассмотренным моделям.
6. Простейшая модель прогнозирования (без тренда) с мультипликативными коэффициентами сезонности Уинтерса имеет вид:
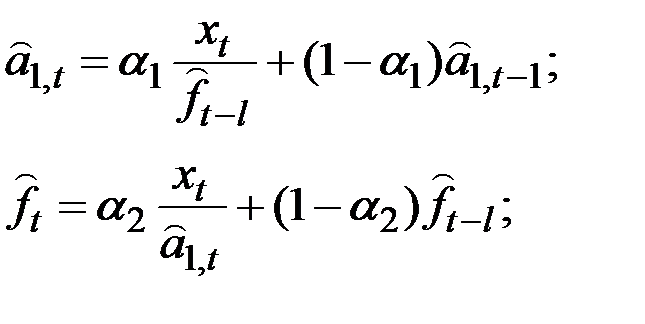
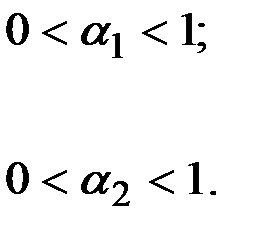
Прогноз следующего значения ряда:
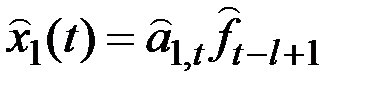 .
.
Более общее выражение для прогноза на 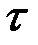 шагов вперёд:
шагов вперёд:
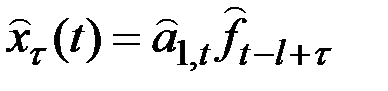 ,
, 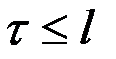 .
.
Величины 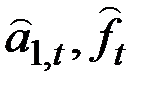 могут быть записаны через прошлые данные и начальные условия:
могут быть записаны через прошлые данные и начальные условия:
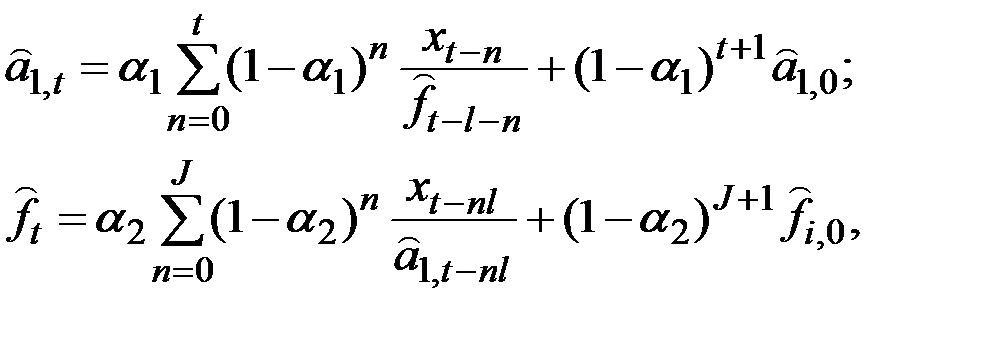
где 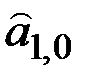 – начальные значения
– начальные значения 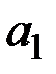 ;
; 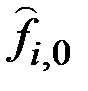 – начальное значение
– начальное значение 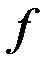 в соответствующей
в соответствующей 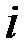 фазе (месяце) цикла (года);
фазе (месяце) цикла (года);  – наибольшая целая часть t / l.
– наибольшая целая часть t / l.
Прогноз является функцией всех прошлых значений фактического ряда, параметров 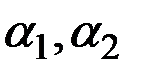 и начальных условий
и начальных условий 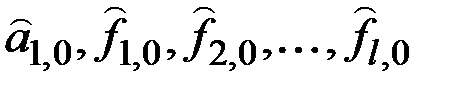 .
.
7. Полная сезонная модель Уинтерса с линейным ростом аналогична только что рассмотренной:
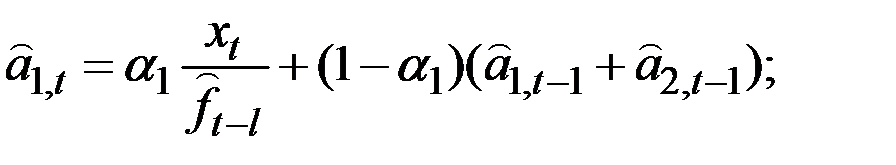
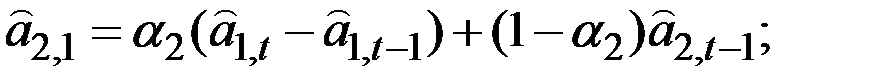
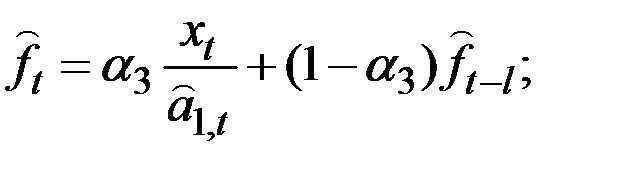
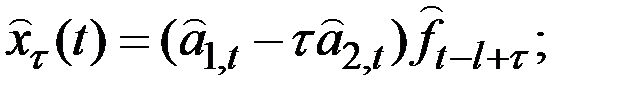
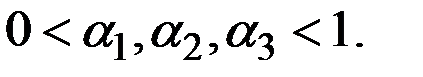
Единственным изменением в выражении для 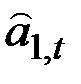 является добавление
является добавление 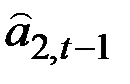 наиболее поздней оценки аддитивного фактора роста, характеризующего изменение среднего за полный сезонный цикл уровня процесса за единицу времени (месяц). Выражение для обновления коэффициента сезонности остаётся тем же, что и раньше. Оценки
наиболее поздней оценки аддитивного фактора роста, характеризующего изменение среднего за полный сезонный цикл уровня процесса за единицу времени (месяц). Выражение для обновления коэффициента сезонности остаётся тем же, что и раньше. Оценки 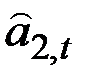 модифицируются по аналогичной процедуре экспоненциального сглаживания.
модифицируются по аналогичной процедуре экспоненциального сглаживания.
Прогноз является здесь функцией прошлых и текущих данных, параметров 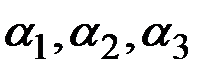 и первоначальных значений
и первоначальных значений 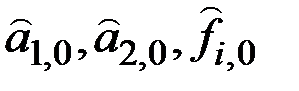 .
.
Качество и точность прогнозов зависит от этих факторов.
8. Аддитивная модель сезонных явлений Г.Тейла и С. Вейджа.
Построение такой модели имеет целью упрощение процедуры прогнозирования, поскольку комбинация мультипликативной сезонной модели с линейным ростом математически громоздка. Кроме того, на практике чаще встречаются экспоненциальные тенденции, чем линейные.
Поэтому замена значений первоначального временного ряда их логарифмами преобразует экспоненциальную тенденцию в линейную и одновременно мультипликативную сезонную модель в аддитивную.
Тогда временной ряд (исходный или преобразованный) можно представить следующим образом:
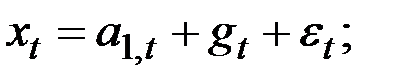
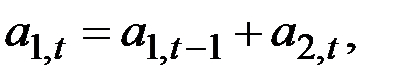
где 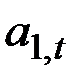 – величина уровня процесса после элиминирования сезонных колебаний;
– величина уровня процесса после элиминирования сезонных колебаний; 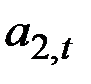 – аддитивный коэффициент роста;
– аддитивный коэффициент роста;
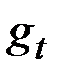 – аддитивный коэффициент сезонности;
– аддитивный коэффициент сезонности; 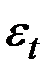 – белый шум.
– белый шум.
Рассмотрим адаптивную процедуру обновления значения 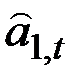 .
.
В момент t мы располагаем наблюдением 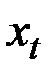 , о котором известно, что
, о котором известно, что 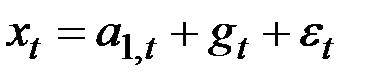 .
.
Однако о шуме и сезонном факторе 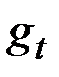 никакой информации нет.
никакой информации нет.
Величину 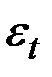 заменим нулём, а в качестве заменителя для
заменим нулём, а в качестве заменителя для 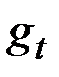 возьмём самую последнюю оценку сезонного фактора
возьмём самую последнюю оценку сезонного фактора 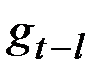 , где l – период сезонного цикла. Величину
, где l – период сезонного цикла. Величину 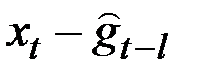 будем рассматривать как новое “фактическое” значение
будем рассматривать как новое “фактическое” значение 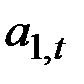 .
.
Последней оценкой уровня 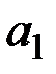 является
является 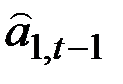 , но она соответствует моменту
, но она соответствует моменту 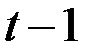 , а не t, поэтому необходимо к
, а не t, поэтому необходимо к 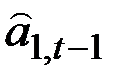 добавить ещё
добавить ещё 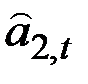 .
.
Но так как оценку 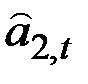 мы ещё не можем получить, то вместо неё берём, оценку
мы ещё не можем получить, то вместо неё берём, оценку 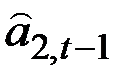 , полученную на предыдущем шаге.
, полученную на предыдущем шаге.
Это приводит к следующей процедуре адаптации:
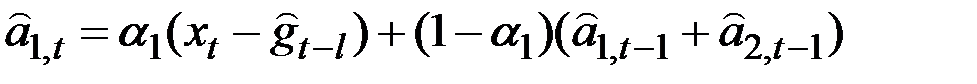 ,
,
которая при данных весах 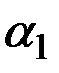 и
и 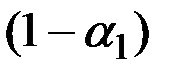 оценивает
оценивает 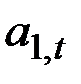 через наиболее свежее наблюдение
через наиболее свежее наблюдение 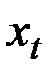 и ранее подсчитанные величины
и ранее подсчитанные величины
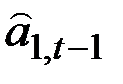 ,
, 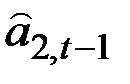 ,
, 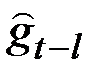 .
.
Учитывая выражение для 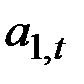 и вычитая из полученного
и вычитая из полученного 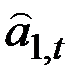 прежнюю оценку
прежнюю оценку 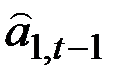 , можем получить оценку
, можем получить оценку 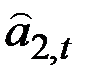 .
.
Однако, поскольку вычисления 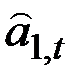 появляются несовершенными, в частности потому, что не принимались в расчёт остатки, то, очевидно, лучше не полагаться на эту разность полностью, а считать её “фактическим” свидетельством динамики ряда и объединить со старым значением
появляются несовершенными, в частности потому, что не принимались в расчёт остатки, то, очевидно, лучше не полагаться на эту разность полностью, а считать её “фактическим” свидетельством динамики ряда и объединить со старым значением 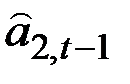 по известной формуле экспоненциального сглаживания
по известной формуле экспоненциального сглаживания
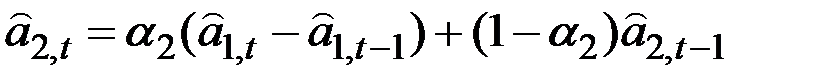 ,
,
где 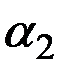 и
и 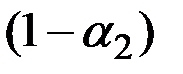 – веса двух источников информации.
– веса двух источников информации.
Наконец, та же процедура применяется для получения оценки 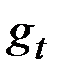 .
.
Новое “фактическое” значение сезонного фактора будет 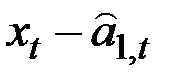 , старое значение равно
, старое значение равно 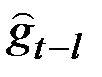 , экспоненциально–сглаженное значение
, экспоненциально–сглаженное значение
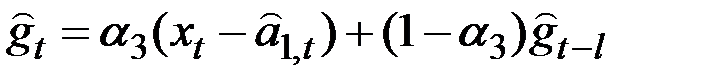 .
.
Все три параметра сглаживания будут удовлетворять условию
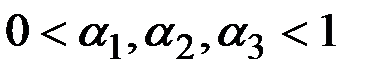 .
.
Адаптивное прогнозирование теперь провести сравнительно просто.
Предположим, что t – текущий момент времени, так что 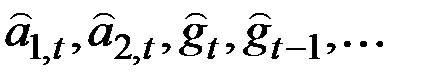 имеются в нашем распоряжении.
имеются в нашем распоряжении.
Предположим также, что мы хотим получить прогноз величины 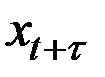 (прогноз на
(прогноз на 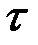 шагов вперёд).
шагов вперёд).
Экстраполируем тенденцию линейного роста, используя самое последнее значение коэффициента 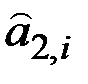 , добавляем самую свежую оценку сезонного члена для этой фазы цикла и пренебрегаем шумом.
, добавляем самую свежую оценку сезонного члена для этой фазы цикла и пренебрегаем шумом.
В результате получаем
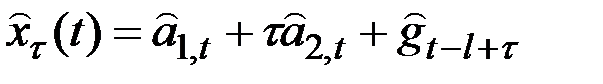
при условии, 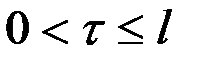 .
.
Если 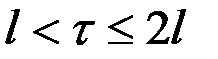 , то необходимо
, то необходимо 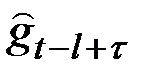 заменить на
заменить на 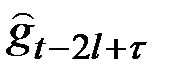 и т.д.
и т.д.
На практике удобнее осуществлять адаптивное регулирование 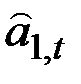
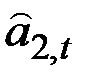 и
и 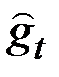 с помощью уравнений, связывающих эти величины с ошибкой прогноза, сделанного в конце периода
с помощью уравнений, связывающих эти величины с ошибкой прогноза, сделанного в конце периода 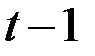 на один шаг вперёд.
на один шаг вперёд.
Уравнение для 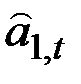 можно переписать следующим образом:
можно переписать следующим образом:
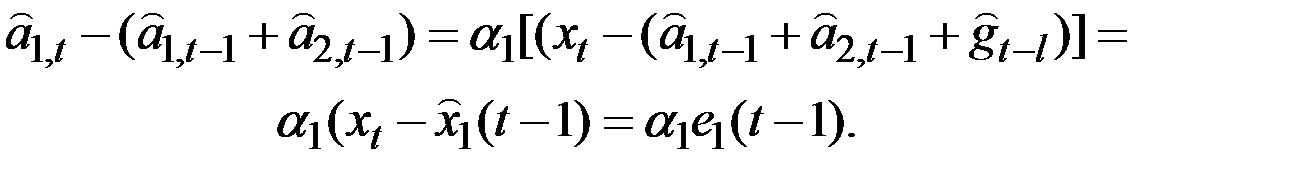
Из предыдущих уравнений легко получить:
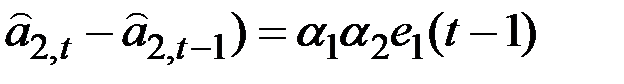 ;
;
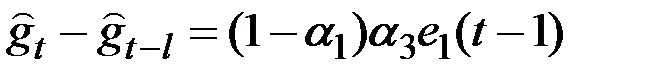 .
.
Корректировки всех параметров модели совпадают по знаку и пропорциональны по величине ошибке последнего прогноза на один шаг вперёд. Коэффициентами пропорциональности будут 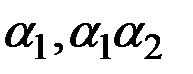 и
и 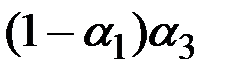 соответственно. Можно заметить, что указанная процедура адаптации является рекурсивной в том смысле, что для определения
соответственно. Можно заметить, что указанная процедура адаптации является рекурсивной в том смысле, что для определения 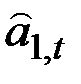 используются прошлые данные о сезонных колебаниях и коэффициенте роста.
используются прошлые данные о сезонных колебаниях и коэффициенте роста.
Оценка 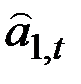 используется для получения новых значений
используется для получения новых значений 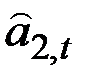 и
и 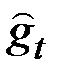 .
.
Но очевидно, что прошлые значения сезонного фактора и коэффициента роста при вычислении 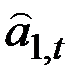 являются лишь суррогатом; не лучше ли было использовать более свежие, текущие оценки этих компонент?
являются лишь суррогатом; не лучше ли было использовать более свежие, текущие оценки этих компонент?
Рассмотрим такой вариант. Вместо выражения для 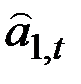 имеем:
имеем:
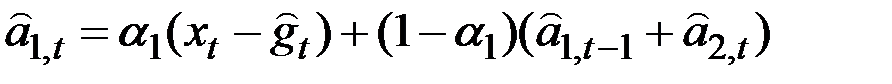 .
.
В другом виде можно записать следующим образом:
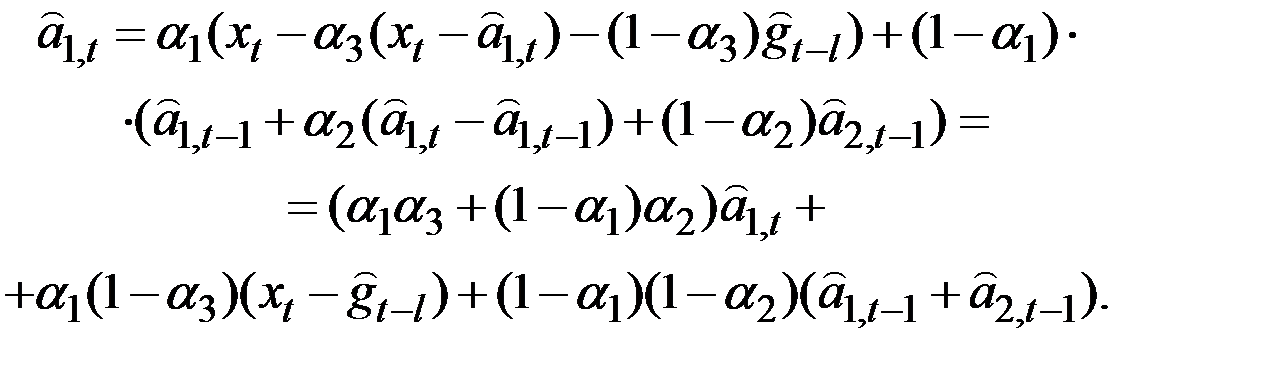
Отсюда получаем:
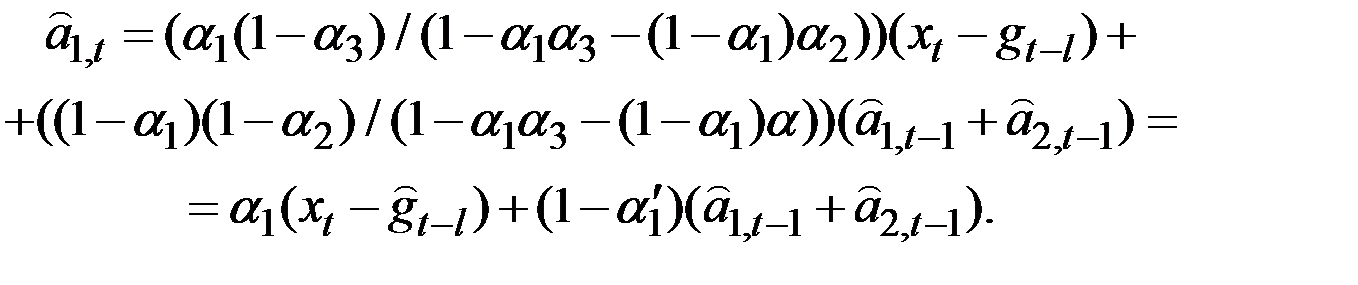
При этом 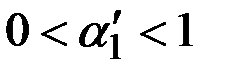 .
.
Общая форма выражения, как видим, та же, что и раньше.
В выражениях лишь 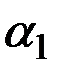 меняется на
меняется на 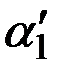 , в остальном они остаются без изменений. Отметим, что
, в остальном они остаются без изменений. Отметим, что 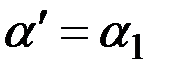 при
при 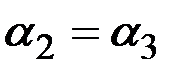 .
.
8. Альтернативы моделей
Возможно множество комбинаций различных типов тенденций и циклических явлений аддитивного и мультипликативного вида.
Представим девять возможных моделей, которые обобщённо выражены одной формулой. Девять упомянутых моделей составляют три группы по три варианта в каждой. Первая группа – модели без тренда. Вторую группу составляют три модели из первой группы, но с аддитивным линейным трендом. В третью группу входят три модели из первой группы, но с мультипликативным (экспоненциальным) трендом.
Все девять моделей могут быть отражены в одной общей записи
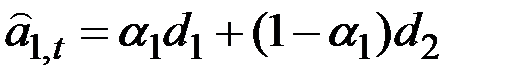 ,
,
где 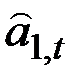 – уровень ряда после элиминирования сезонных колебаний;
– уровень ряда после элиминирования сезонных колебаний;
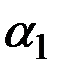 – параметр сглаживания,
– параметр сглаживания, 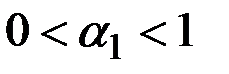 .
.
Значения 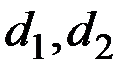 даны в табл. 5.1.
даны в табл. 5.1.
Рассмотрим величины, соответствующие в формуле символам 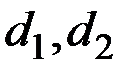 :
:
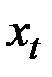 – фактическое наблюдение;
– фактическое наблюдение;
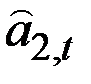 – коэффициент линейного роста, оценивается по формуле:
– коэффициент линейного роста, оценивается по формуле:
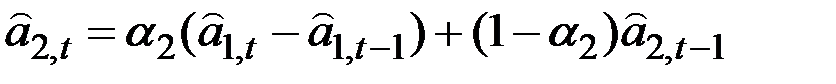 ,
, 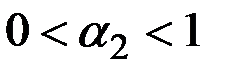 ;
;
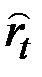 – коэффициент экспоненциального роста:
– коэффициент экспоненциального роста:
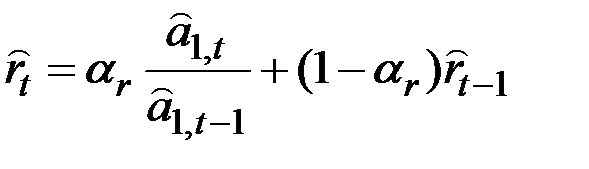 ,
, 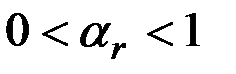 ;
;
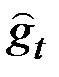 – аддитивная сезонная компонента, определяется по формуле:
– аддитивная сезонная компонента, определяется по формуле:
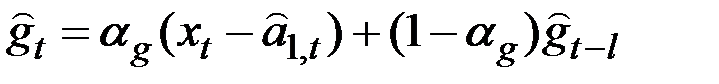 ,
, 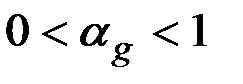 ;
;
 – периодичность сезонного явления;
– периодичность сезонного явления;
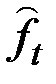 – мультипликативный коэффициент сезонности, подсчитывается по формуле:
– мультипликативный коэффициент сезонности, подсчитывается по формуле: 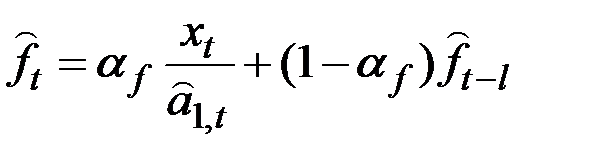 ,
, 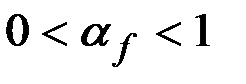 .
.
Прогнозы фактических значений, ожидаемых в момент 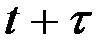 , могут быть получены по общей формуле
, могут быть получены по общей формуле 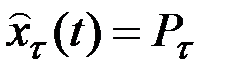 ,
,
где 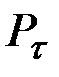 подсчитывается для каждой модели способом табл. 5.2.
подсчитывается для каждой модели способом табл. 5.2.
Таблица 5.1
Значения символов обобщающей формулы
| Характер | 1 | 2 | 3 | ||
| сезонности
Тенденция роста | Отсутствие сезонного эффекта | Аддитивный сезонный эффект | Мультипли–кативный сезонный эффект | ||
| А | Отсутствие | 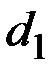
| 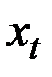
| 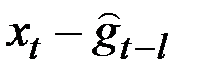
| 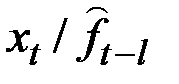
|
| тенденции роста | 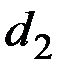
| 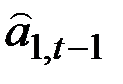
| 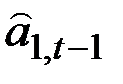
| 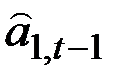
| |
| B | Аддитивный | 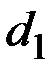
| 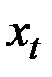
| 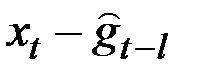
| 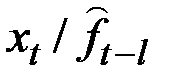
|
| рост | 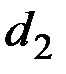
| 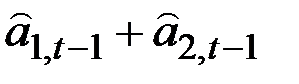
| 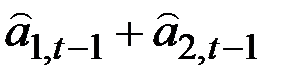
| 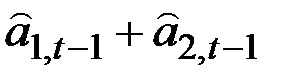
| |
| С | Экспоненци– | 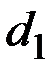
| 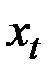
| 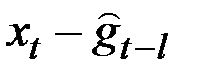
| 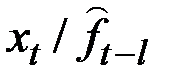
|
| альный рост | 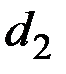
| 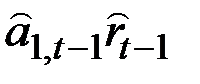
| 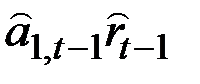
| 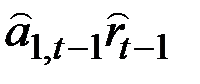
| |
Таблица 5.2
Формулы для прогнозов
| Характер | 1 | 2 | 3 | |
| сезонности
Тенденция роста | Отсутствие сезонного эффекта | Аддитивный сезонный эффект | Мультипликативный сезонный эффект | |
| A | Отсутствие тенденции роста | 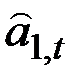
| 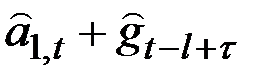
| 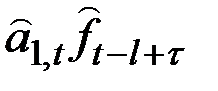
|
| B | Аддитивный рост | 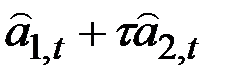
| 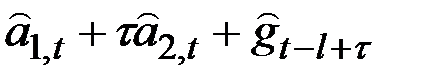
| 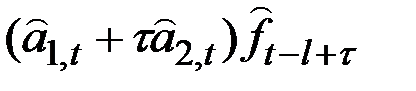
|
| C | Экспонен– циальный рост | 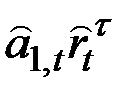
| 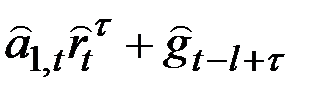
| 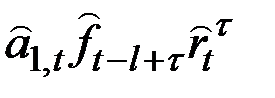
|
10. Многократное сглаживание
Понятие экспоненциальной средней 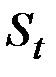 для временного ряда
для временного ряда 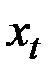 можно обобщить на случай экспоненциальных средних более высоких порядков. Экспоненциальная средняя произвольного р–го порядка определяется как
можно обобщить на случай экспоненциальных средних более высоких порядков. Экспоненциальная средняя произвольного р–го порядка определяется как 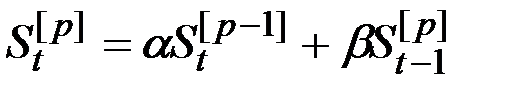 ,
,
где 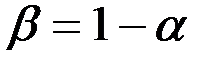 ; p = 1, 2, ..., n;
; p = 1, 2, ..., n; 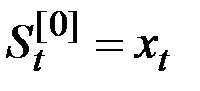 ;
;
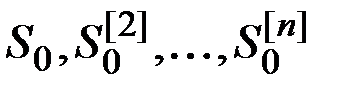 – начальные значения экспоненциальных средних соответствующего порядка.
– начальные значения экспоненциальных средних соответствующего порядка.
В общем случае принимается гипотеза, что исследуемый процесс является параболой n–го порядка, а прогноз на t шагов вперёд выражается формулой
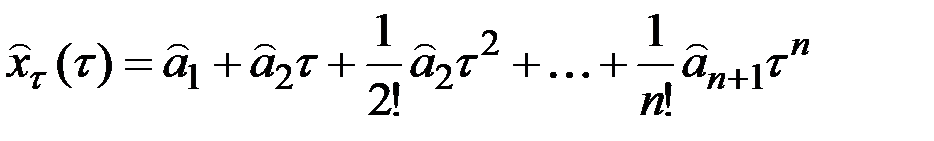 ,
,
где параметры 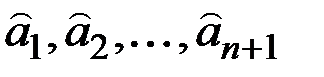 нужно определить.
нужно определить.
Идея экспоненциального предсказания основана на том, что прогноз осуществляется полиномом, представляющим первые n+1 членов разложения процесса 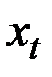 в ряд Тейлора:
в ряд Тейлора:
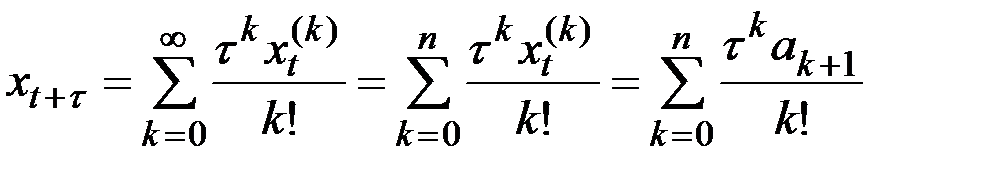 ,
,

|
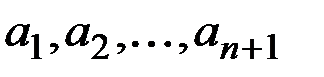 предсказывающего полинома связаны с экспоненциальными средними
предсказывающего полинома связаны с экспоненциальными средними 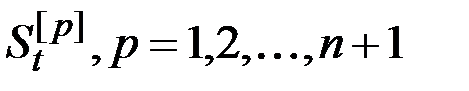 соотношением
соотношением
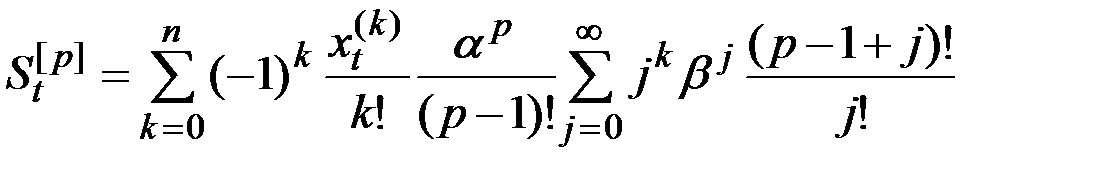 ;
; 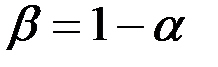 .
.
Таким образом, имеем 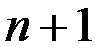 уравнение, дающее сглаженные значения
уравнение, дающее сглаженные значения 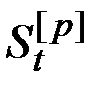 через линейные комбинации производных
через линейные комбинации производных 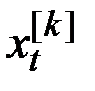 .
.
Линейные уравнения для сглаженных величин можно записать в компактной форме, используя матрицы.
Пусть S  будет вектором S
будет вектором S  =
= 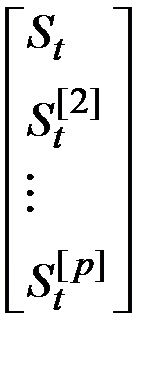 и пусть
и пусть 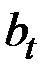 будет вектором
будет вектором 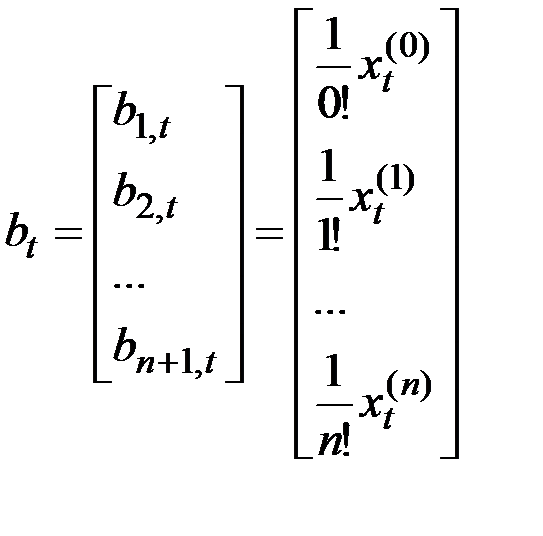 коэффициентов в разложении Тейлора.
коэффициентов в разложении Тейлора.
Тогда можно записать: 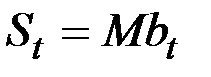 ,
,
где M – матрица (n+1) (n+1) с элементами, содержащими бесконечные суммы степеней постоянной сглаживания:
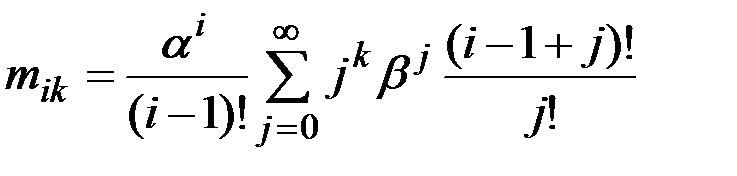 .
.
Система n+1 линейных уравнений может быть разрешима относительно коэффициентов предсказывающего полинома по формуле
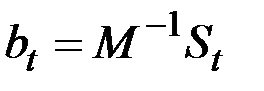 .
.
Для экстраполяции трендов обычно используются полиномы не выше второго порядка. Для этих случаев элементы обратной матрицы определяются аналитически как функции постоянной сглаживания 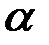 .
.
Для любой последовательности наблюдений полином P степени n , полученный с помощью многократного сглаживания, является решением, которое минимизирует взвешенную сумму квадратов ошибок:
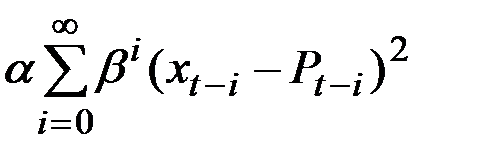 .
.
Надо отметить, что для сглаженных величин S 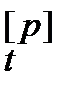 , р = 1, 2, …, n+1 должны быть установлены начальные значения.
, р = 1, 2, …, n+1 должны быть установлены начальные значения.
Простейший путь задания исходных условий – оценка коэффициентов полинома разложения. Если имеются выборочные данные, то эти оценки могут быть получены методом наименьших квадратов, как это делается в регрессионном анализе.
Для новых временных рядов коэффициенты должны быть предсказаны или на основе аналогии с другими подобными рядами, или исходя из ожидаемых характеристик моделируемого процесса. В том и другом случае должны быть некие начальные оценки этих коэффициентов.
Приведём формулы расчёта по адаптивным полиномиальным моделям. Во всех рассматриваемых случаях предполагается, что тренд может быть представлен полиномом и наблюдается при наличии шума:
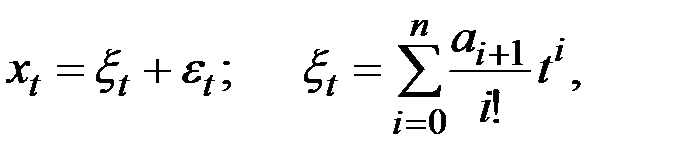
где 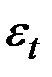 – белый шум.
– белый шум.
Ожидаемое значение х  в момент Т+ t будем обозначать
в момент Т+ t будем обозначать 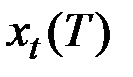 , где t – время упреждения, на которое делается прогноз;
, где t – время упреждения, на которое делается прогноз;
T – текущий момент времени.
Адаптивная полиномиальная модель нулевого порядка: n = 0
Гипотеза: 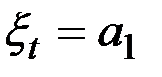 .
.
Экспоненциальная средняя: 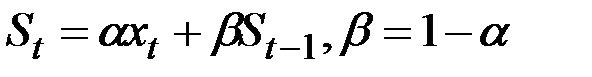 .
.
Начальное условие: 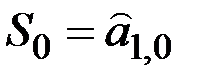 .
.
Оценка коэффициента: 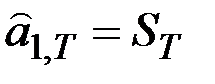 .
.
Прогноз: 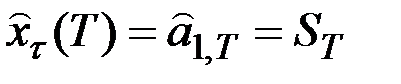 .
.
Адаптивная полиномиальная модель первого порядка: n = 1
Гипотеза: 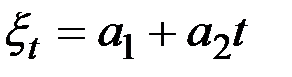 .
.
Экспоненциальные средние: 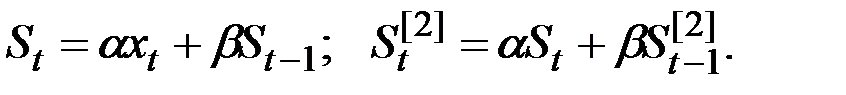
Начальные условия: 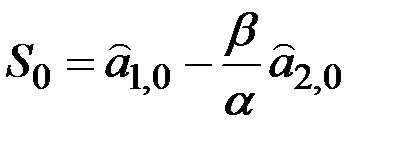 ;
; 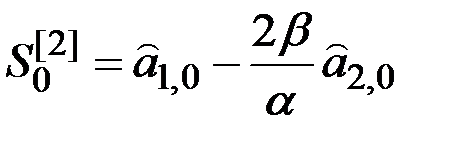 .
.
Оценки коэффициентов: 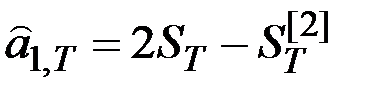 ;
; 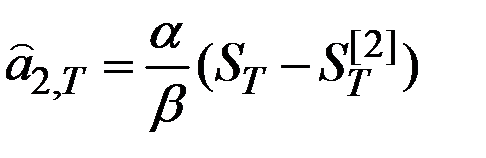 .
.
Прогноз: 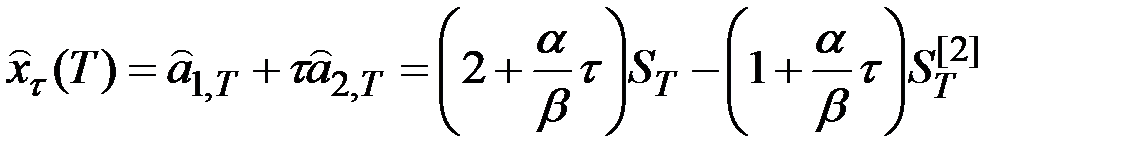 .
.
Адаптивная полиномиальная модель второго порядка: n = 2
Гипотеза: 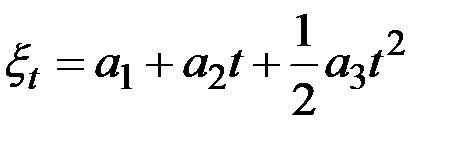 .
.
Экспоненциальные средние: 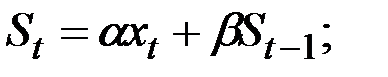
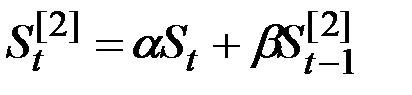 ;
;
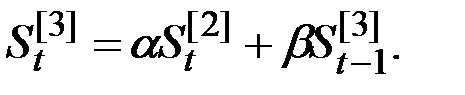

|
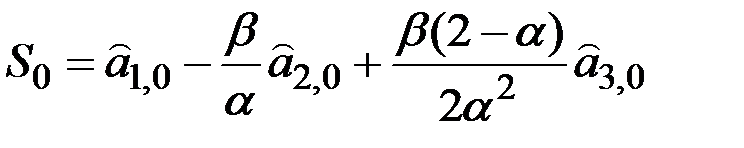 ;
;
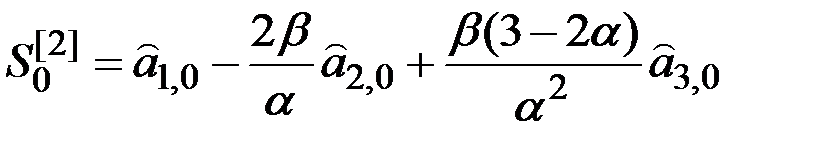 ;
;
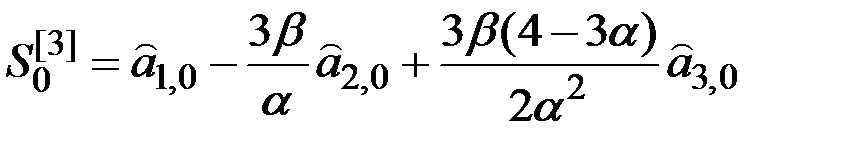 .
.
Оценка коэффициентов:
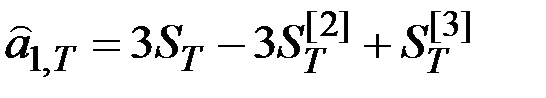 ;
;
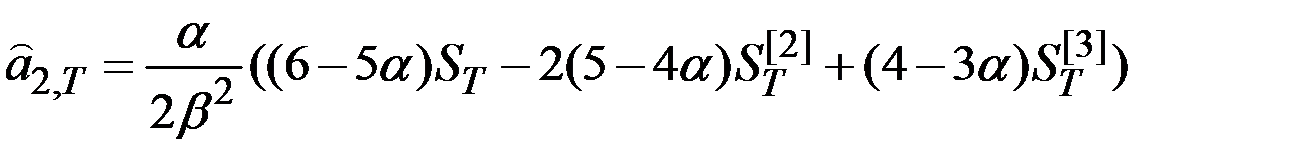 ;
;
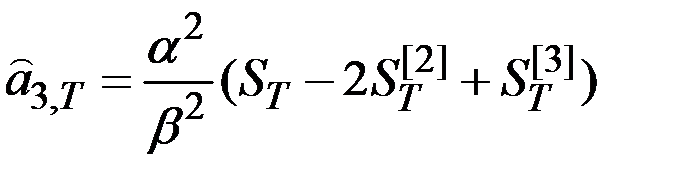 .
.
Прогноз:
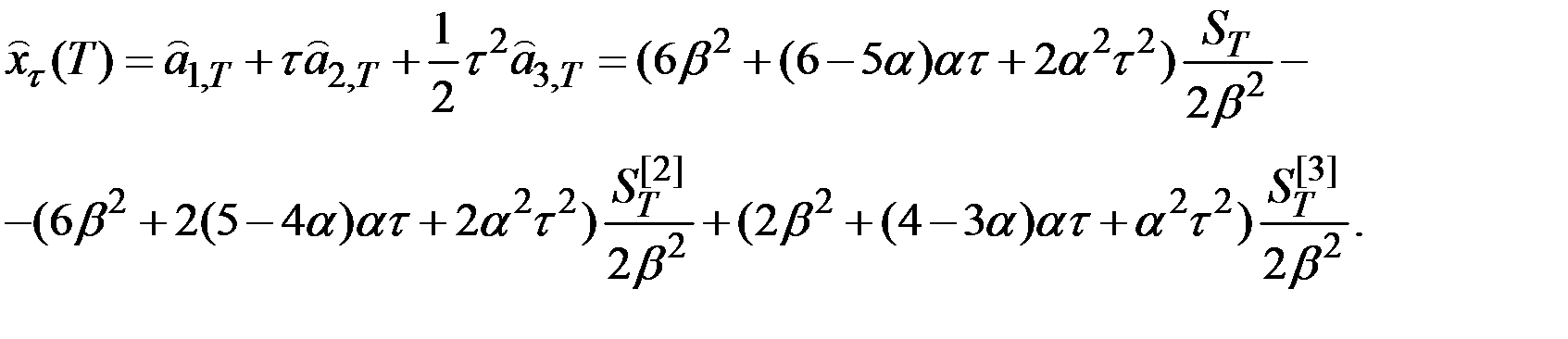
Пример 5.2. Имеются условные данные о стоимости акций некоторой компании за 16 кварталов (табл. 5.3).
Таблица 5.3
Стоимость акций некоторой компании за 16 кварталов
| Квартал t
| Стоимость акций | Расчётные значения 8 уровней ряда | Коэффициенты модели Хольта–Уинтерса | Модель Хольта–Уинтерса
| ||
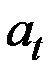
| 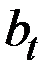
| 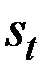
| ||||
| 1 | 304 | 308,65 | 310,73 | 9,22 | 0,9723 | 297,32 |
| 2 | 320 | 317,25 | 320,87 | 9,50 | 0,9947 | 316,97 |
| 3 | 334 | 325,85 | 329,58 | 9,26 | 1,0157 | 336,68 |
| 4 | 347 | 334,45 | 338,54 | 9,17 | 1,0258 | 348,02 |
| 5 | 323 | 343,05 | 343,06 | 7,77 | 0,9538 | 338,08 |
| 6 | 342 | 351,65 | 348,74 | 7,14 | 0,9862 | 348,94 |
| 7 | 365 | 360,25 | 356,92 | 7,45 | 1,0199 | 361,47 |
| 8 | 375 | 368,85 | 364,73 | 7,56 | 1,0272 | 373,77 |
| 9 | 342 | 368,17 | 6,32 | 0,9389 | 355,09 | |
| 10 | 365 | 373,18 | 5,93 | 0,9813 | 369,52 | |
| 11 | 378 | 376,56 | 5,17 | 1,0103 | 386,65 | |
| 12 | 399 | 383,74 | 5,77 | 1,0347 | 392,11 | |
| 13 | 363 | 388,64 | 5,51 | 0,9360 | 365,71 | |
| 14 | 388 | 394,52 | 5,62 | 0,9826 | 386,78 | |
| 15 | 419 | 404,52 | 6,93 | 1,0256 | 404,26 | |
| 16 | 418 | 409,21 | 6,26 | 1,0268 | 425,73 | |
Спрогнозировать цены на эти акции на 4 квартала пятого года.
Решение. Используем мультипликативную тренд–сезонную модель Хольта–Уинтерса с линейным ростом.
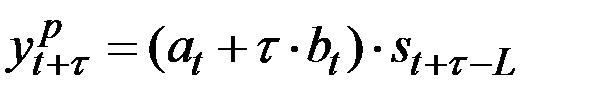 .
.
Здесь:
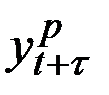 – расчётное (прогнозное) значение показателя для периода
– расчётное (прогнозное) значение показателя для периода 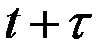 ;
; 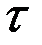 – период упреждения;
– период упреждения;
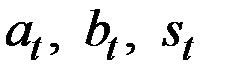 – коэффициенты модели (они адаптируются, уточняются по мере перехода от членов ряда с номером t–1 к t);
– коэффициенты модели (они адаптируются, уточняются по мере перехода от членов ряда с номером t–1 к t);
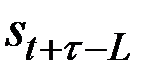 – значение коэффициента сезонности того периода, для которого рассчитывается показатель;
– значение коэффициента сезонности того периода, для которого рассчитывается показатель;
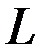 – период сезонности.
– период сезонности.
Уточнение (адаптация к новому значению параметра времени t) коэффициентов производится с помощью формул:
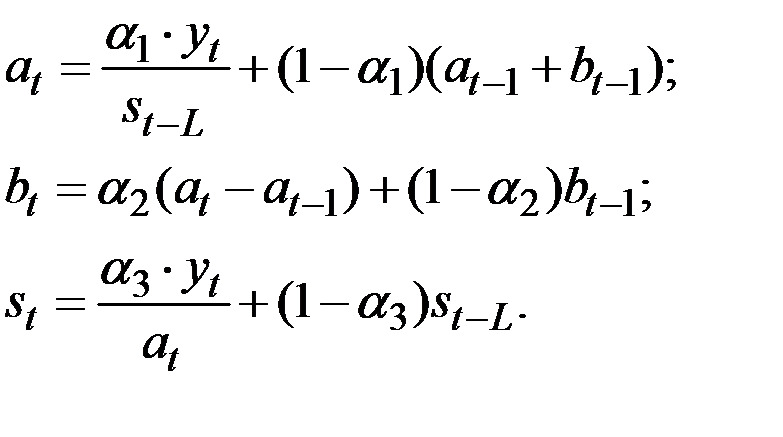
Параметры сглаживания 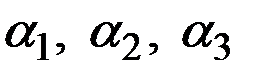 подбираются путём перебора так, чтобы расчётные данные наилучшим образом соответствовали фактическим.
подбираются путём перебора так, чтобы расчётные данные наилучшим образом соответствовали фактическим.
Для расчёта 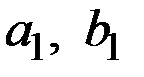 необходимо оценить значения этих коэффициентов для предыдущего периода времени ( для t = 0).
необходимо оценить значения этих коэффициентов для предыдущего периода времени ( для t = 0).
Для оценки этих величин 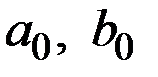 применим линейную модель к первым 8 значениям исходного ряда
применим линейную модель к первым 8 значениям исходного ряда 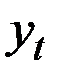 . Линейная модель имеет вид:
. Линейная модель имеет вид:
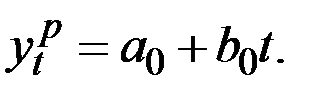
Метод наименьших квадратов даёт возможность определить коэффициенты этой модели по формулам:
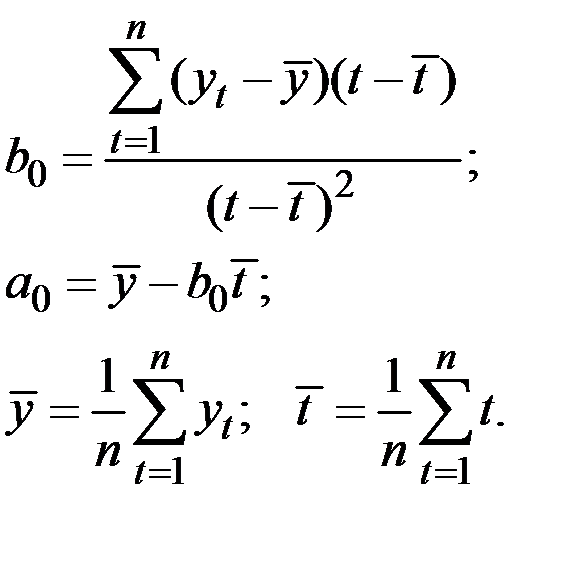
Применяя линейную модель к первым 8 значениям исходного ряда 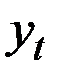 находим:
находим: 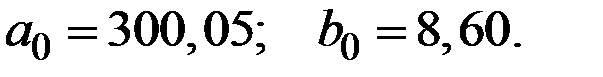
С учётом полученных коэффициентов линейная модель имеет вид:
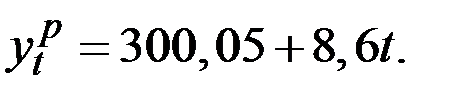
Из этого уравнения находим расчётные значения 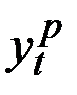 и сопоставляем их с фактическими. Такое сопоставление позволяет оценить приближённые значения коэффициентов сезонности четырёх кварталов
и сопоставляем их с фактическими. Такое сопоставление позволяет оценить приближённые значения коэффициентов сезонности четырёх кварталов 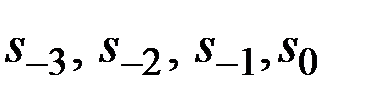 для года предшествующего первому году наблюдений.
для года предшествующего первому году наблюдений.
Эти значения необходимы для расчёта коэффициентов сезонности первого года 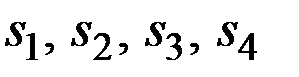 и для других параметров модели Хольта–Уинтерса.
и для других параметров модели Хольта–Уинтерса.
Коэффициент сезонности есть отношение фактического значения показателя к значению, рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности первого квартала может служить отношение фактических и расчётных значений показателя 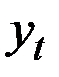 первого квартала первого года, равное
первого квартала первого года, равное 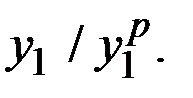 Такое же отношение и для первого квартала второго года, т.е. за 5–й квартал (
Такое же отношение и для первого квартала второго года, т.е. за 5–й квартал ( 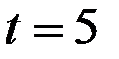 )
) 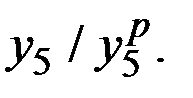 Для окончательной, более точной, оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин:
Для окончательной, более точной, оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин:
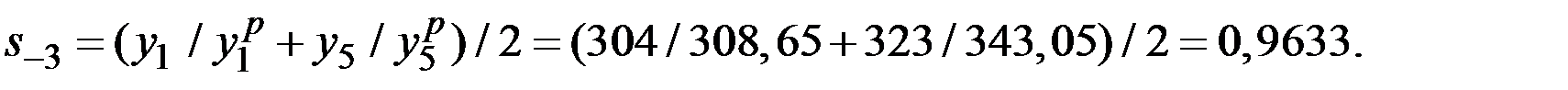
Аналогично находим оценки коэффициентов сезонности для второго, третьего и четвёртого кварталов:
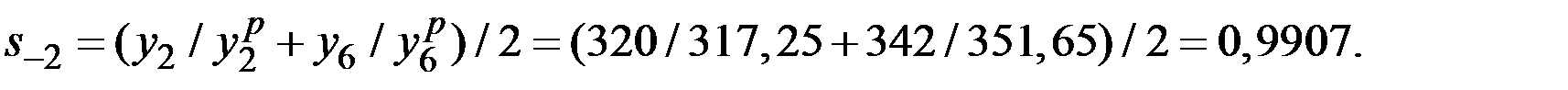
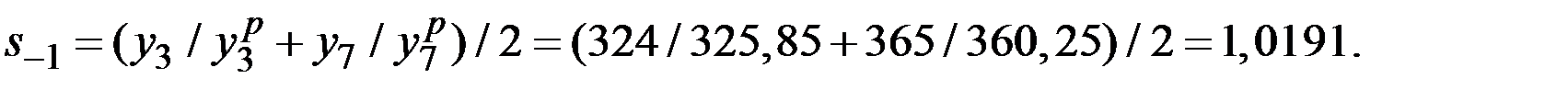
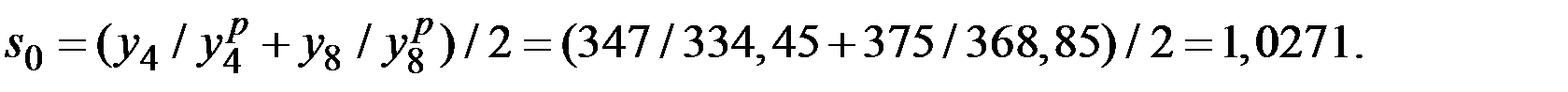
Оценив значения 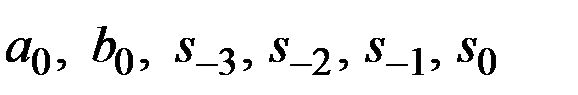 можно перейти к построению адаптивной мультипликативной модели Хольта–Уинтерса.
можно перейти к построению адаптивной мультипликативной модели Хольта–Уинтерса.
Путём перебора возможных значений параметров сглаживания было установлено, что лучшими являются следующие их значения:
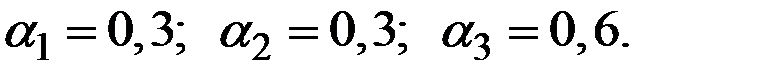
Рассчитаем значения 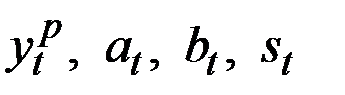 для
для 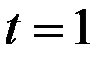
Полагая 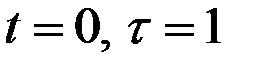 находим из исходного уравнения метода:
находим из исходного уравнения метода:
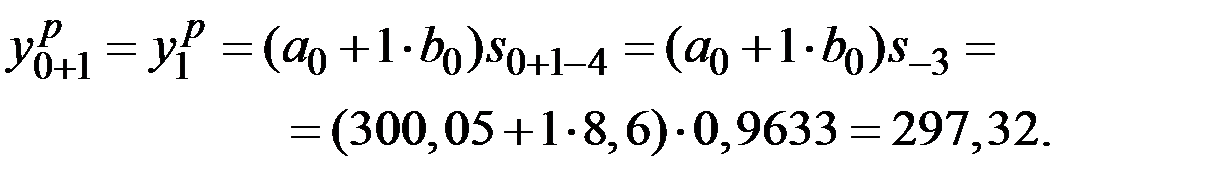
Уточняем параметры адаптации (полагая 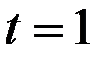 ):
):
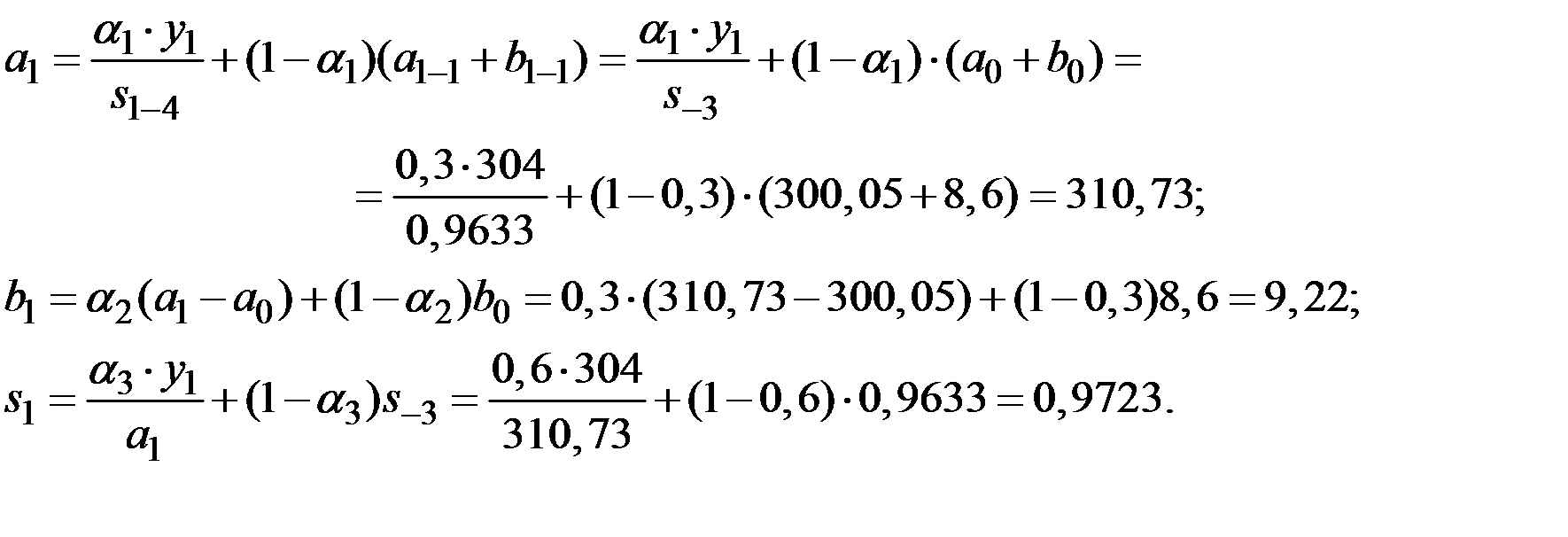
Рассчитаем значения 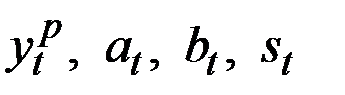 для
для 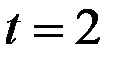 (полагая в правой части формул
(полагая в правой части формул 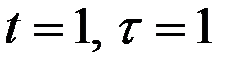 ):
):
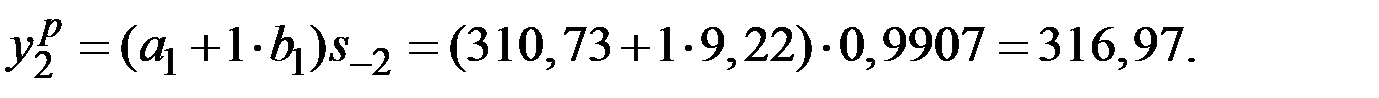

Рассчитаем значения 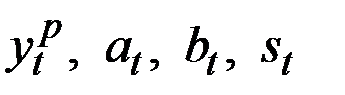 для
для 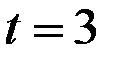 (полагая в правой части формул
(полагая в правой части формул 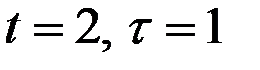 ):
):
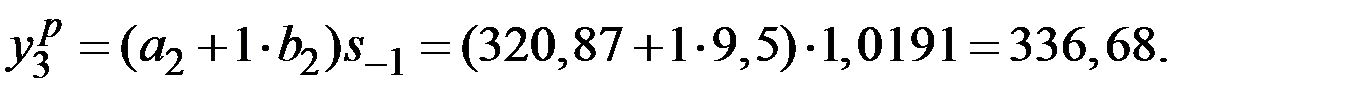

Рассчитаем значения 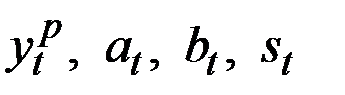 для
для 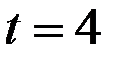 (полагая в правой части формул
(полагая в правой части формул 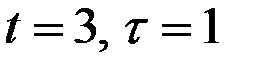 ):
):
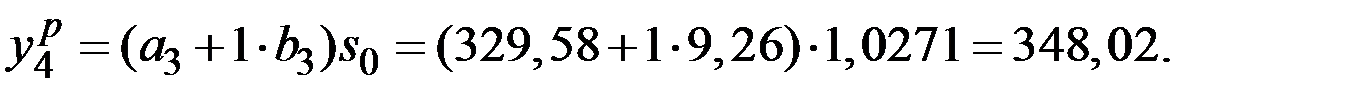
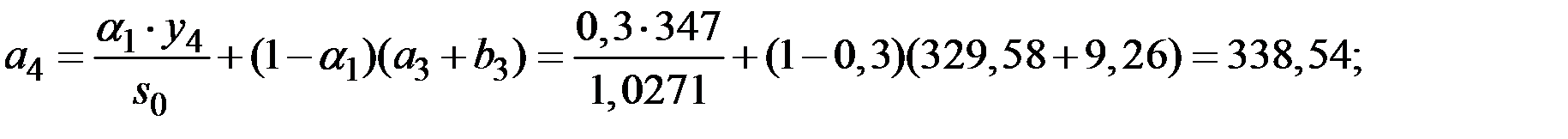
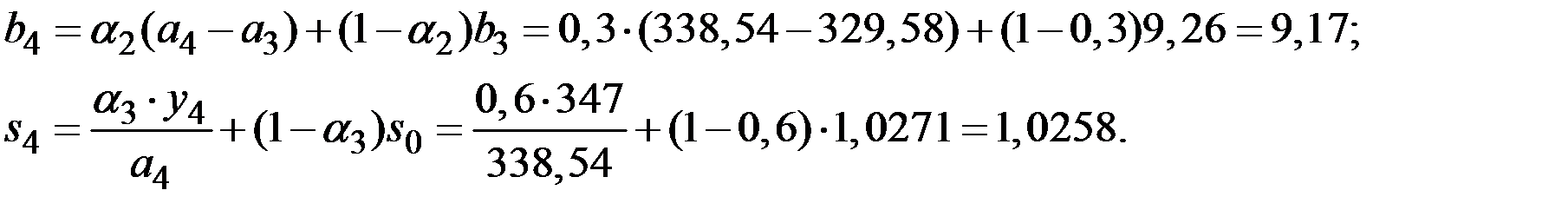
Рассчитаем значения 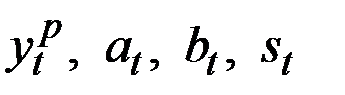 для
для 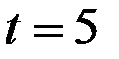 (полагая в правой части формул
(полагая в правой части формул 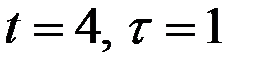 ).
).
Здесь и в дальнейшем используются коэффициенты сезонности, уточнённые в предыдущем году.
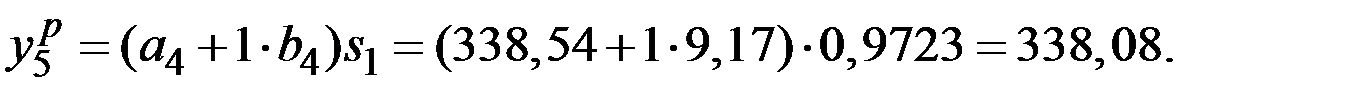
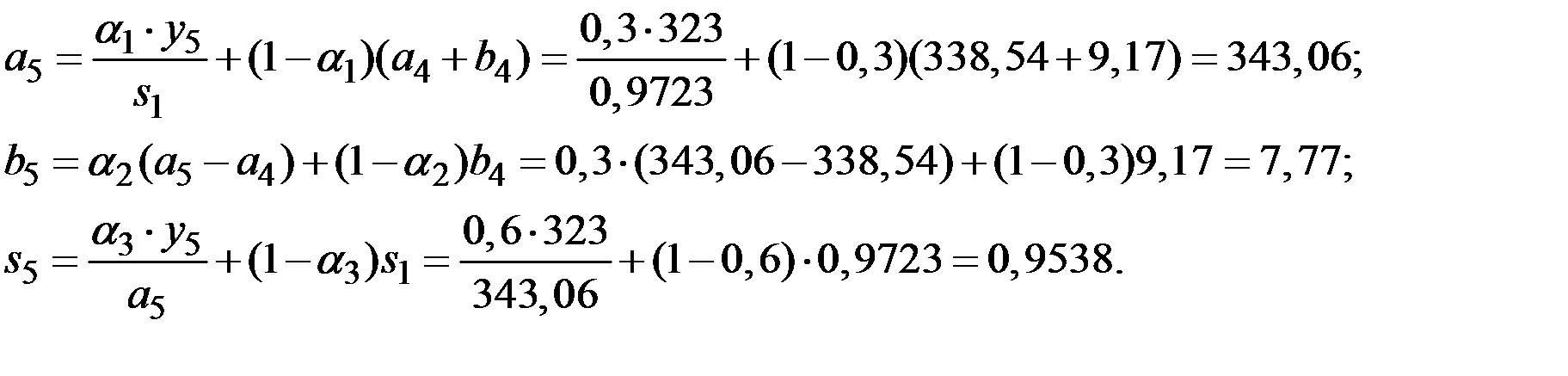
Продолжая аналогично для 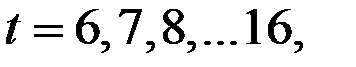 строят адаптивную мультипликативную модель Хольта–Уинтерса (табл. 5.4).
строят адаптивную мультипликативную модель Хольта–Уинтерса (табл. 5.4).
Максимальное значение  , для которого можно находить коэффициенты модели равно количеству имеющихся данных по показателю
, для которого можно находить коэффициенты модели равно количеству имеющихся данных по показателю 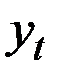 . У нас максимальное значение
. У нас максимальное значение 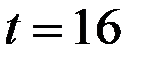 .
.
Таблица 5.4
Стоимость акций некоторой компании за 16 кварталов
Квартал

| Стоимость
акций
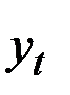
| Модель
Хольта–Уинтерса
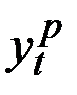
| Абсолютная
погрешность
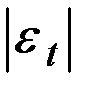
| Относительная погрешность 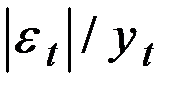
| Точки поворота |
| 1 | 304 | 297,32 | 6,68 | 2,20 | – |
| 2 | 320 | 316,97 | 3,03 | 0,95 | 0 |
| 3 | 334 | 336,68 | –2,68 | 0,80 | 1 |
| 4 | 347 | 348,02 | –1,03 | 0,29 | 1 |
| 5 | 323 | 338,08 | –15,08 | 4,67 | 1 |
| 6 | 342 | 348,94 | –6,94 | 2,03 | 0 |
| 7 | 365 | 361,47 | 3,53 | 0,97 | 1 |
| 8 | 375 | 373,77 | 1,23 | 0,33 | 0 |
| 9 | 342 | 355,09 | –13,09 | 3,83 | 1 |
| 10 | 365 | 369,52 | –4,32 | 1,18 | 1 |
| 11 | 378 | 386,65 | –8,65 | 2,29 | 1 |
| 12 | 399 | 392,11 | 6,89 | 1,73 | 1 |
| 13 | 363 | 365,71 | –2,71 | 0,75 | 1 |
| 14 | 388 | 386,78 | 1,22 | 0,31 | 0 |
| 15 | 419 | 404,26 | 14,74 | 3,52 | 1 |
| 16 | 418 | 425,73 | –7,73 | 1,85 | – |
Проверка качества модели. Для того чтобы модель была качественной уровни (значения) остатков 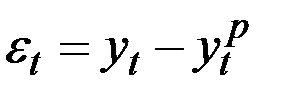 (разности между фактическими и расчётными значениями) должны удовлетворять определённым условиям (точности и адекватности). Для проверки этих условий сведём необходимые данные в табл. 5.4.
(разности между фактическими и расчётными значениями) должны удовлетворять определённым условиям (точности и адекватности). Для проверки этих условий сведём необходимые данные в табл. 5.4.
1. Проверка точности модели. Будем считать, что условие точности выполнено, если относительная погрешность в среднем не превышает 5%.
Вычислим относительная погрешность как отношение абсолютного отклонения показателя к его фактическому значению:
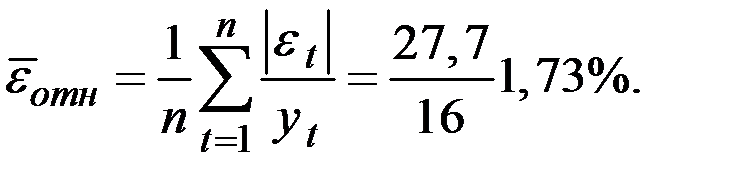
Условие точности выполнено
Дата: 2019-03-05, просмотров: 899.