Модель экономического роста Солоу названа в честь американского экономиста Роберта Солоу и была разработана в 1950–1960 годах.
Модель Солоу до сих пор она остаётся главной теоретической базой для анализа связей между накоплением капитала, технологическим прогрессом, ростом населения и экономическим ростом. За свои работы Роберт Солоу был удостоен в 1987 году Нобелевской премии.
В 1920–1950 годах реальные процессы экономического роста неплохо описывали кейнсианские модели Домара и Харрода.
Кейнсианскими моделями экономического роста называют модели, в которых кейнсианские предпосылки и методы анализа экономической конъюнктуры в коротком периоде используются для описания экономических процессов в долгосрочном периоде.
Р. Харрод и Е. Домар независимо друг от друга построили простейшую модель экономического роста, соответствующую кейнсианской концепции функционирования национальной экономики.
Но для более поздних наблюдений наиболее успешно использовалась неоклассическая модель экономического роста Р. Солоу.
Различают два основных пути экономического роста.
Экстенсивный путь предполагает простое количественное увеличение факторов производства без их качественного изменения.
Интенсивный путь означает, что экономический рост происходит за счёт совершенствования и повышения эффективности использования факторов производства.
Задачами модели Солоу являются ответы на следующие вопросы:
1) каковы факторы сбалансированного экономического роста,
2) как достичь экономического равновесия,
3) какой темп роста может позволить себе экономика при заданных параметрах экономической системы, и как при этом максимизируются доходы населения и объём потребления,
4) какая часть произведённого продукта должна потребляться сегодня, а какая его часть должна сберегаться для использования в будущем.
В модели Солоу источниками экономического роста являются:
1) накопление капитала,
2) рост населения,
3) технологический прогресс.
Исследуем влияние каждого источника на обеспечение более высокого уровня жизни, увеличение масштабов совокупного производства и потребления в стране, то есть на экономический рост.
Основными характеристиками неоклассических моделей экономического роста являются:
1) предположение о функционировании экономики в условиях совершенной конкуренции, обеспечивающей гибкую систему цен и равенство цен факторов производства их предельной производительности;
2) отсутствие функции совокупного спроса, поскольку гибкая система цен постоянно приравнивает объём совокупного спроса к объёму совокупного предложения;
3) отсутствие функции инвестиций, так как при равновесии на рынке благ инвестиции равны сбережениям;
4) представление технологии в виде производственной функции с взаимозаменяемыми факторами производства и постоянным эффектом масштаба.
Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Он использовал в своей модели функцию Кобба–Дугласа, в которой труд и капитал являются основными факторами.
Другими предпосылками анализа модели Солоу являются: убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
Взаимозаменяемость факторов (изменение капиталовооружённости) объясняется не только технологическими (техническими) условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов производства.
Модель Солоу показывает, как сбережения, рост населения и технологический прогресс (источники роста) воздействуют на рост объёма производства во времени.
1. Сначала проанализируем, как спрос и предложение товаров определяют параметры процесса накопления капитала. Для этого будем считать неизменными объём трудовых ресурсов и используемую технологию.
В модели Солоу важны спрос и предложение на рынке произведённой продукции. Предложение определяет объём производства в каждый момент времени, а спрос определяет распределение продуктов производства между различными направлениями использования.
Предложение товаров в модели Солоу описывается с помощью производственной функции Y = F(K , L). То есть объём производства зависит от запасов капитала и используемого труда.
Производственная функция в модели Солоу обладает свойством постоянной отдачи от масштаба:
zY = F(zK , zL),
где z – любое положительное число.
Для простоты соотнесём все величины с количеством работников.
Примем z = 1/ L. Тогда получим: Y / L = F(K / L, 1).
Уравнение показывает, что объём производства в расчёте на одного работника (Y / L) является функцией капитала на одного работника (K / L).
Обозначим: y = Y / L – выпуск продукции на одного работника,
k = K / L – капитал, приходящийся на одного работника, то есть капиталовооружённость.
Тогда производственную функцию можно записать как
y = f(k), где f(k) = F(k,1).
График этой функции показывает, как капиталовооружённость k определяет размер выпуска продукции на одного работника: y = f(k).
Тангенс угла наклона этого графика равен предельной производительности капитала.
В модели Солоу спрос на товары предъявляется со стороны потребителей и инвесторов: y = c + i .
Модель предполагает, что функция потребления принимает форму:
,
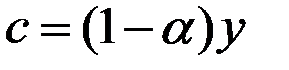где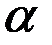 
– норма сбережения.
Тогда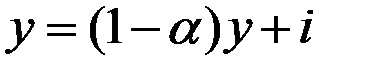 
, или 
.
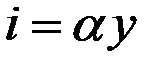Это уравнение показывает, что инвестиции (как и потребление) пропорциональны доходу.
Если инвестиции равны сбережениям, норма сбережений также показывает, какая часть продукции направляется на капитальные вложения.
2. Представив две главные составляющие модели Солоу (производственную функцию и функцию потребления) можно проанализировать, как накопление капитала обеспечивает экономический рост.
Запасы капитала могут изменяться по двум причинам:
1) инвестиции приводят к росту запасов капитала;
2) часть капитала амортизируется, что уменьшает его запасы.
Так как 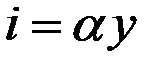, то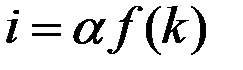 
.
Чем выше уровень капиталовооружённости k, тем выше объём производства и больше инвестиции.
Чтобы учесть в модели амортизацию, предположим, что ежегодно выбывает определённая доля капитала δ (δ – норма выбытия).
Количество капитала, выбывающего за год, составляет δ k.
Выразим влияние инвестиций и выбытия на запасы капитала:
,
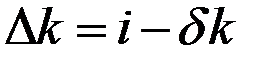где Δk – изменение запасов капитала на одного работника.
Иначе можно записать:
.
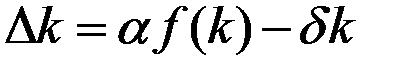На рис. 3.6 показано, что существует единственный уровень капиталовооружённости k *, при котором инвестиции равны величине износа.
Если в экономике достигнут именно такой уровень, то он не будет изменяться во времени.
При данном уровне капиталовооружённости Δk = 0.
Эта ситуация называется состоянием устойчивой капиталовооружённости k *.
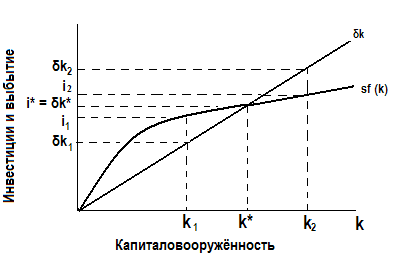
Рис. 3.6. Инвестиции, выбытие капитала и устойчивый
уровень капиталовооружённости
При k < k * инвестиции превышают выбытие, а запасы капитала растут, при k > k * инвестиции меньше выбытия, и запасы уменьшаются.
Устойчивый уровень капиталовооружённости соответствует равновесию экономики в долгосрочном периоде.
Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния.
Когда возрастает норма сбережений, то последствия такого изменения можно увидеть на рис. 3.7.
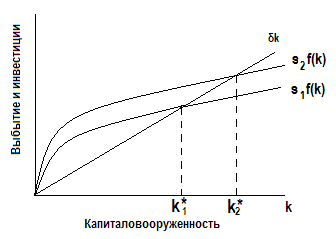
Рис. 3.7. Влияние роста нормы сбережений
Предположим, что экономика начинает развиваться, находясь в устойчивом состоянии при норме сбережений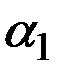 
и запасах капитала k1*.
Норма сбережений затем возрастает до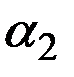 
, вызывая соответствующий сдвиг вверх кривой 
.
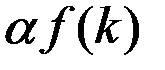Сразу после повышения нормы сбережений инвестиции увеличиваются, но запас капитала и, следовательно, выбытие остаются пока неизменными. В итоге инвестиции превышают выбытие капитала.
Капитал будет постепенно расти до тех пор, пока экономика не достигнет нового устойчивого состояния k2* с большей капиталовооружённостью и более высокой производительностью труда.
Модель Солоу показывает, что норма сбережений предопределяет величину устойчивой капиталовооружённости.
Если норма сбережения более высока, то экономика будет иметь больший запас капитала и более высокий уровень производства.
Увеличение нормы сбережений обеспечивает рост до тех пор, пока экономика не достигнет нового устойчивого состояния.
Если в экономике поддерживается высокая норма сбережений, то и капиталовооружённость, и производительность будут высоки. Но сохранить высокие темпы экономического роста навечно не удастся.
3. Согласно модели Солоу каждому уровню нормы сбережения соответствует определённое устойчивое состояние. Поэтому возникает проблема выбора оптимальной нормы сбережения.
Делая выбор в пользу того или иного устойчивого состояния, политик, преследующий цель максимизации экономического благосостояния общества, захочет выбрать устойчивое состояние с наивысшим уровнем потребления.
Уровень накопления капитала, обеспечивающий устойчивое состояние с наивысшим уровнем потребления, называется Золотым уровнем накопления капитала. Обозначим его k**.
Чтобы найти потребление в устойчивом состоянии, преобразуем тождество y = с + i. Получим: с = y – i .
Заменим значения y и i на их величины в условиях устойчивого уровня капиталовооружённости.
Тогда потребление на одного работника в устойчивом состоянии можно выразить как
c* = f(k*) – δk*.
Это равенство показывает, что увеличивающаяся капиталовооружённость двояко воздействует на величину потребления: она способствует росту выпуска продукции, но в то же время большее количество продукции требуется для возмещения выбытия капитала.
Рис. 3.8 показывает, что существует единственный уровень капиталовооружённости k** – уровень Золотого правила, при котором душевое потребление достигает максимума.
Обозначим через с** потребление по Золотому правилу.
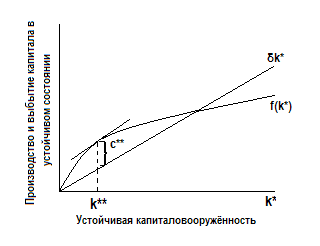
Рис. 3.8. Устойчивый уровень потребления по Золотому правилу
Когда начальная капиталовооружённость выше, чем по Золотому правилу, достижение устойчивого состояния с максимумом потребления сопровождается более высоким уровнем потребления.
Когда же начальная капиталовооружённость ниже, чем по Золотому правилу, достижение устойчивого состояния по Золотому правилу требует немедленного снижения потребления в настоящем для того, чтобы повысить его в будущем.
4. Базовая модель Солоу показывает, что процесс накопления капитала и увеличение нормы сбережения показывают лишь переход от одного состояния равновесия к другому.
Поэтому для дальнейшего анализа модели Солоу поочерёдно снимем две предпосылки: неизменность численности населения (и его занятой части) и отсутствие технологического (технического) прогресса.
Сначала введём фактор роста населения.
Предположим, что население растёт с постоянным темпом n.
Это новый фактор, влияющий вместе с инвестициями и выбытием на капиталовооружённость: рост численности работников ведёт к сокращению капиталовооружённости каждого из них:
Δk = i – δk – nk .
Инвестиции увеличивают k, а выбытие капитала и рост населения уменьшают её. Для того чтобы воспользоваться этим равенством, заменим i на 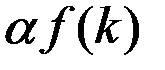и получим:
.
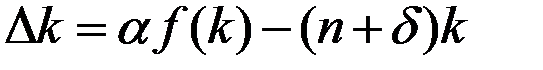Это уравнение показывает, что выбытие уменьшает k за счёт сокращения запасов капитала, в то время как рост населения уменьшает k, распределяя капитал между большим количеством работающих.
Составляющую (δ + n)k можно рассматривать как критическую величину инвестиций – это инвестиции, необходимые для поддержания запаса капитала, приходящегося на одного работника, на постоянном уровне.
На рис. 3.9 показана ситуация, отражённая на рис. 3.6, но усложнённая за счёт включения эффекта роста населения.
Для того чтобы экономика была в устойчивом состоянии, инвестиции 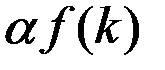должны компенсировать последствия выбытия капитала и роста населения – (δ + n)k, что представлено на графике точкой пересечения двух кривых.
Так, в точке k* величина Δk = 0 и i* = δ k* + nk*.
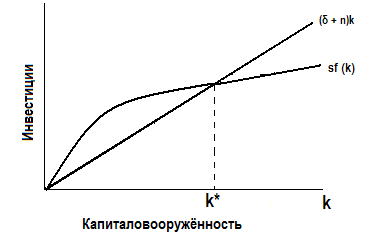
Рис. 3.9. Учёт роста населения в модели Солоу
Рост населения дополняет исходную модель Солоу по трём направлениям.
1. Рост населения позволяет приблизиться к выяснению причин экономического роста, так как он объясняет непрерывный рост валового выпуска продукции.
2. Рост населения влияет на уровень накопления капитала по Золотому правилу. Потребление на одного работника равно с = y – i.
Поскольку устойчивый объём производства – это f(k*), а инвестиции устойчивого состояния – это (δ + n)k*, то устойчивый уровень потребления можно определить как
c* = f(k*) – (δ + n)k*.
3. Рост населения позволяет дать дополнительное объяснение того, почему некоторые страны богаты, а другие – бедны.
На рис. 3.10 показано, что увеличение темпа прироста населения с n1 до n2 уменьшает капиталовооружённость устойчивого состояния с k1* до k2*.
Если k* уменьшается, а y* = f(k*), то производительность y* тоже снижается.
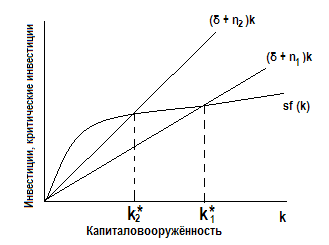
Рис. 3.10. Влияние роста населения на состояние равновесия
Так модель Солоу предсказывает, что страны с более высоким темпом роста населения будут иметь меньшую капиталовооружённость и, следовательно, более низкий уровень доходов на душу населения.
5. Теперь включим в модель Солоу технологический прогресс – третий источник экономического роста. Для этого запишем производственную функцию следующим образом:
Y = F(K , L × E),
где E – эффективность труда одного работника. Она зависит от здоровья, образования и квалификации рабочей силы.
Составляющая L × E представляет собой рабочую силу, измеренную в единицах труда с неизменной эффективностью.
В соответствии с новой производственной функцией общий объём производства Y зависит от количества единиц капитала K и от числа эффективных единиц рабочей силы, то есть от L × E = L ×(1 + g).
Простейшим допущением технологического прогресса является то, что он вызывает прирост эффективности труда E с постоянным темпом g.
Например, если g = 0,02, то отдача от каждой единицы труда увеличивается на 2% в год: объём производства возрастает так, как если бы рабочая сила за год выросла на 2%.
Эта форма технологического прогресса называется трудосберегающей, а g называется темпом трудосберегающего технологического прогресса.
Поскольку рабочая сила L растёт с темпом n, а отдача от каждой единицы труда E растёт с темпом g, то общее количество эффективных единиц труда L × E растёт с темпом (n + g).
Пусть k = K /(L × E) есть капитал на единицу труда с постоянной эффективностью, a y = Y /(L × E) – объём производства на единицу труда с постоянной эффективностью.
Поэтому можно записать: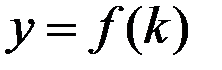 
.
Анализ экономики происходит по той же схеме, что и в случае с ростом населения. Уравнение, показывающее изменение k с течением времени, теперь выглядит следующим образом:
.
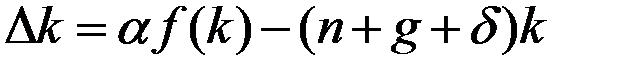Если величина g велика, то общее количество единиц труда с постоянной эффективностью растёт быстро, а прирост капитала на такую единицу труда сравнительно мал и может стать отрицательным.
На рис. 3.11 показано, что имеется один уровень k*, при котором капитал и выпуск на единицу труда постоянны. Это устойчивое состояние представляет собой долгосрочное равновесие экономики.
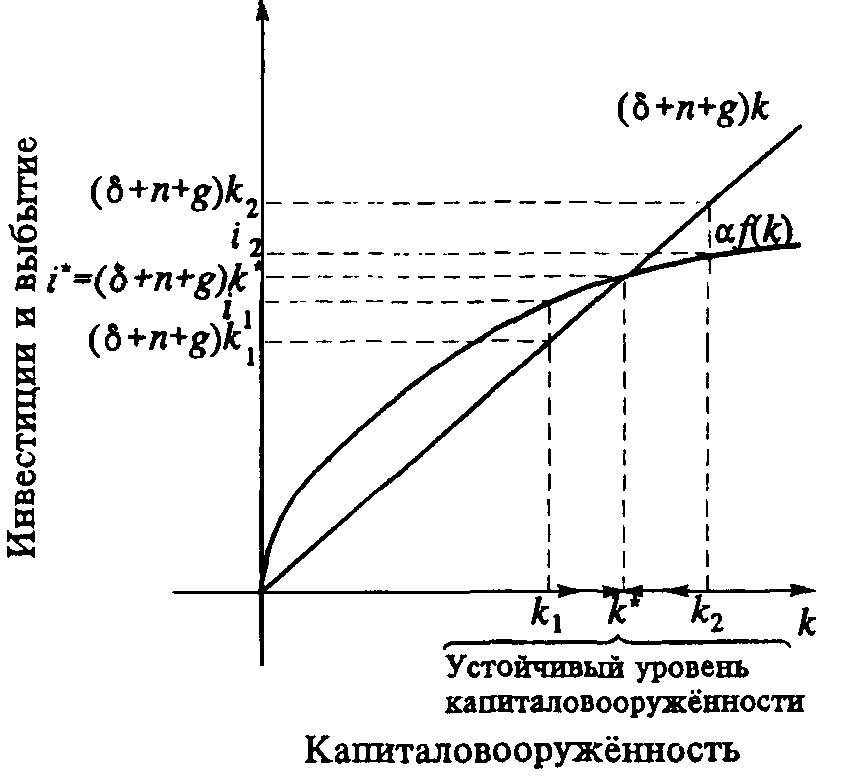
Рис. 3.11. Равновесие при технологическом прогрессе
При устойчивом состоянии экономики инвестиции 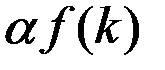в точности компенсируют уменьшение k вследствие выбытия, роста населения и технологического прогресса.
Точка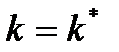 
– это точка равновесия для показателя k, поскольку в этой точке величина удельного прироста капиталовооружённости равна величине её удельного сокращения, и показатель k остаётся неизменным.
Это равновесие устойчиво, поскольку при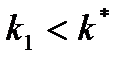 
прирост удельных инвестиций превышает уменьшение капиталовооружённости, и величина капиталовооружённости растёт.
В случае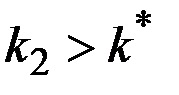 
удельные инвестиции ниже, чем уменьшение капиталовооружённости, и её величина падает, пока не достигнет 
.
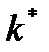Из рис. 3.11 можно видеть, что в случае увеличения нормы сбережения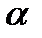 
график функции инвестиций пойдёт выше и, следовательно пересечёт прямую 
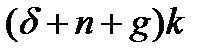правее. Рост нормы сбережения приводит к увеличению устойчивого уровня капиталовооруженности 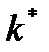, а следовательно, и устойчивого уровня дохода на единицу труда 
.
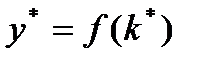«Золотое правило» устойчивого равновесия системы с учётом всех рассмотренных факторов представлено на рис. 3.12.
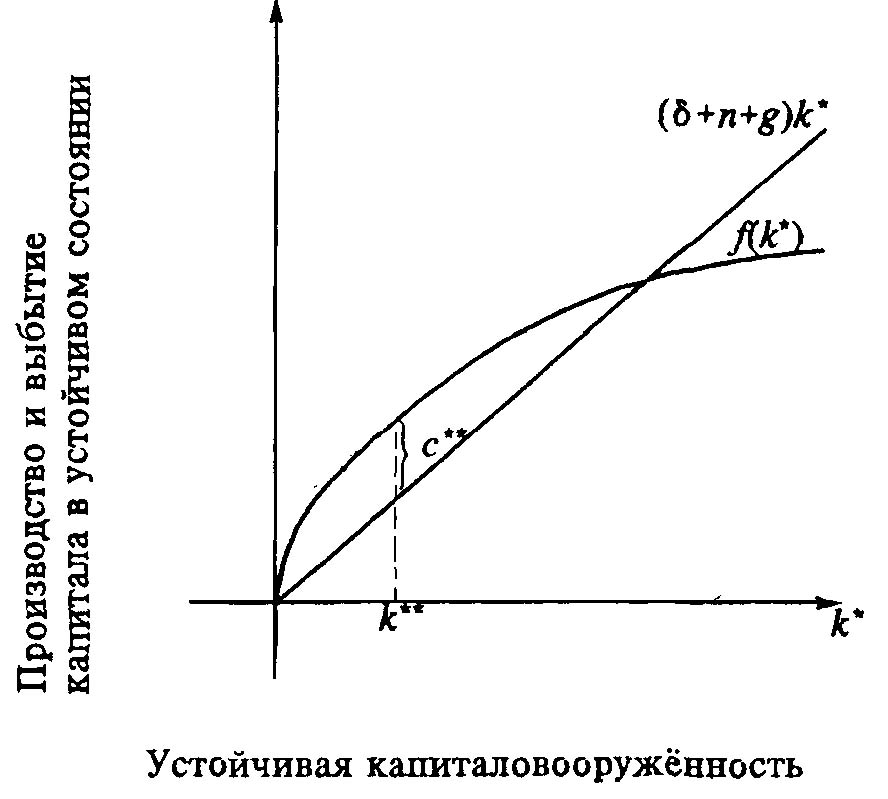
Рис. 3.12. «Золотое правило» устойчивого равновесия системы
Статистика подтверждает, что в странах с более быстрым ростом потребления уровень душевого потребления более низок. Хотя, конечно, в каждой конкретной стране своя производственная функция, норма выбытия и исходное состояние развития (вовсе не обязательно устойчивое).
1. Если первоначальная величина капиталовооружённости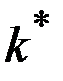 
меньше, чем 
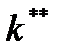, то имеет смысл увеличить норму сбережения до величины, соответствующей Золотому правилу, и постепенно экономика выйдет на максимальный уровень удельного потребления 
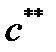. Отметим, однако, что вначале удельный уровень потребления снизится и лишь затем начнёт постепенно расти, наряду с ростом удельных инвестиций и выпуска.
2. Если же первоначальная величина капиталовооружённости 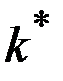больше, чем 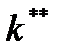, то нужно снизить норму сбережения до уровня, соответствующего Золотому правилу. Тогда экономика также постепенно выйдет на уровень удельного потребления 
.
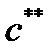В этом случае вначале удельный уровень потребления вырастет, превысив 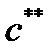, и затем начнёт постепенно снижаться к 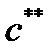, наряду со снижением удельных инвестиций (выросших в начальный момент) и выпуска.
Динамика удельных показателей выпуска (у), потребления (с), инвестиций (i) для двух описанных случаев (рост и снижение нормы сбережения) представлена на рис. 3.13.а и рис. 3.13.б.
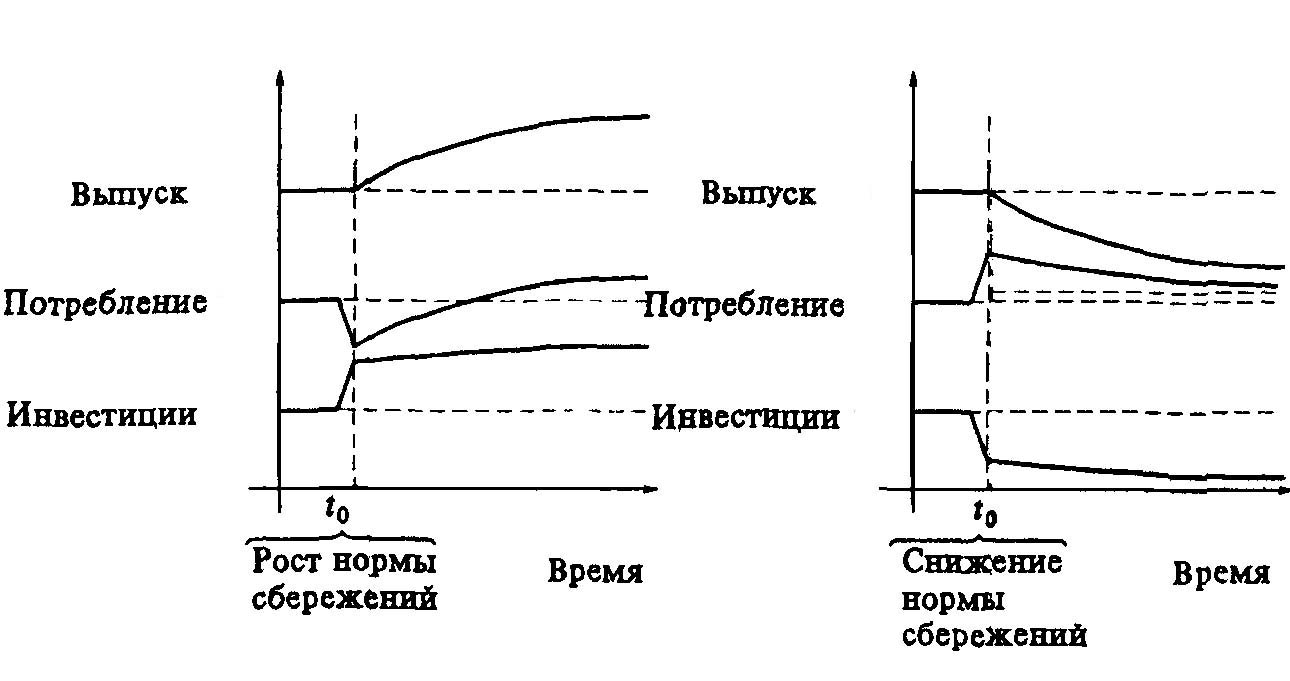
а) рост нормы сбережения б) снижение нормы сбережения
Рис. 3.13. Динамика показателей для двух вариантов развития системы
Таким образом, если нас интересует прежде всего рост потребления в ближайшей перспективе, а не максимальный его равновесный уровень в долгосрочном периоде, то и задача оптимизации должна быть сформулирована по–другому.
Характеристику изменения некоторых переменных модели Солоу с учётом технологического прогресса даёт табл. 3.3. Таким образом, с учётом технологического прогресса модель Солоу в конце концов может объяснить, почему уровень жизни растёт из года в год.
Технологический прогресс может поддерживать непрерывный рост выпуска продукции на одного работника, тогда как высокий уровень сбережений ведёт к высоким темпам роста только до момента достижения устойчивого состояния.
Как только экономика его достигает, темп роста производства на одного работника зависит лишь от скорости технологического прогресса.
Таблица 3.3
Устойчивый рост в модели Солоу с учётом технологического прогресса
| Переменные | Обозначения | Темп прироста |
| Капитал на единицу труда с постоянной эффективностью | k = K /( L × E) | 0 |
| Объём производства на единицу труда с постоянной эффективностью | y = Y /(L × E) = = f(k) | 0 |
| Объём производства на одного работника | Y / L = y×E | g |
| Общий объём производства | Y = y(L × E) | n + g |
Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущий уровень жизни. Введение в модель технологического прогресса изменяет также условия выполнения Золотого правила. Золотое правило для накопления капитала определяет устойчивый уровень, при котором максимизируется потребление на единицу труда с постоянной эффективностью.
Теперь можно выразить этот уровень следующим образом:
c * = f(k *) – (δ + n + g)k*.
Устойчивый уровень потребления максимизируется, если предельная производительность капитала
f ´(k *) = δ + n + g, т.е. f ´(k *) – δ = n + g .
Поскольку в реальных условиях экономика испытывает воздействие как роста населения, так и технологического прогресса, целесообразно использовать это условие для выявления избытка или недостатка капитала по сравнению с устойчивым состоянием по Золотому правилу.
Таким образом, в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости ресурсов.
Если национальная норма сбережений слишком низка, то государственная политика может привести к её увеличению двумя путями: непосредственно, через увеличение государственных сбережений и косвенно – через стимулирование увеличения частных сбережений.
Многие меры государственной политики ориентированы на стимулирование технологического прогресса путём поощрения научных исследований.
С помощью модели Солоу можно решить вопрос об избытке или недостатке капитала в экономике страны.
Модель Солоу можно применить для объяснения экономических процессов, протекающих в стране в разные периоды времени, и для определения оптимального варианта роста с максимизацией потребления.
Однако представленная модель имеет и свои недостатки.
Хотя модель Солоу представляет собой хорошую базу для анализа экономического роста, она является лишь первой его ступенью.
Модель анализирует состояния устойчивого равновесия, достигаемые в длительном периоде, тогда как для экономической политики важна и краткосрочная динамика производства и уровня жизни.
Также модель не включает целый ряд ограничителей роста, существенных в современных условиях – ресурсных, экологических, социальных.
Используемая в модели функция Кобба–Дугласа не всегда отражает реальную ситуацию в экономике.
Именно поэтому учёные, изучающие экономический рост, пытаются построить более сложные модели, которые позволяют исследовать более широкий круг проблем.
Модель Солоу показывает, что продолжительный рост уровня жизни может иметь место только в результате технологического прогресса.
По сравнению с моделью экономического роста Харрода–Домара модель Солоу позволяет более точно описать некоторые особенности макроэкономических процессов.
1. Производственная функция в этой модели нелинейна и обладает свойством убывания предельной производительности.
2. Модель учитывает выбытие основного капитала.
3. В модель Солоу включается описание динамики трудовых ресурсов и технического прогресса и их влияние на экономический рост.
4. В модели Солоу ставится и решается задача максимизации уровня потребления на некотором множестве устойчивых траекторий.
Всё это, конечно, усложняет структуру модели.
Получение точных формул для траекторий изменения основных её показателей становится существенно более сложной задачей.
Поэтому некоторые другие аспекты описываются в базовой модели Солоу упрощённо: считаются постоянными норма сбережений и норма выбытия капитала, инвестиционные лаги отсутствуют, а производственная функция имеет постоянную отдачу от масштаба.
Кроме того, на начальном уровне анализа модели ищутся не траектории изменения всех её показателей (как в модели Харрода–Домара), а характеристики состояний устойчивого равновесия, к которым система выходит в долгосрочном периоде.
С формальной точки зрения это представляет собой более простую задачу.
Пример 3.5. Модель Солоу использует функцию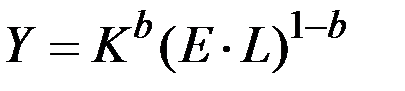 
,
где Y – выпуск, K – капитал,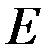 
– параметр эффективности труда, L – труд, 
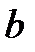– параметр модели. Доля капитала в общем доходе составляет 1/3, темп прироста численности населения равен (4/3)% в год, темп прироста параметра эффективности труда составляет 1,5% в год, норма амортизации составляет 2,5% в год. Определить норму сбережения, потребление на единицу эффективного труда и капиталовооружённость эффективного труда, соответствующие «золотому правилу».
Решение. Основное уравнение динамики в модели Солоу имеет вид
,
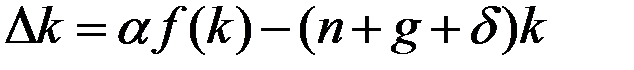где k – капиталовооружённость эффективного труда,
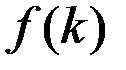– производственная функция в интенсивной форме,
n – темп прироста численности населения,
g – темп прироста параметра эффективности труда,
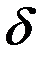– норма амортизации, 
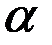– норма накопления.
Для функции Кобба–Дугласа, использованной в задаче, имеем:
.
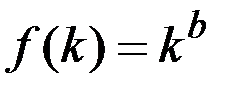На траектории сбалансированного роста (в состоянии устойчивого равновесия для капиталовооружённости)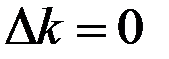 
.
Используя это условие, получаем уравнение, задающее капиталовооружённость эффективного труда на траектории сбалансированного роста:
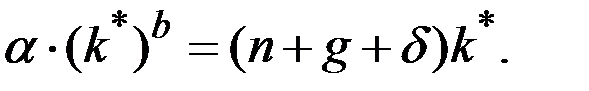
Перегруппировав, получаем капиталовооружённость эффективного труда на траектории сбалансированного роста:
.
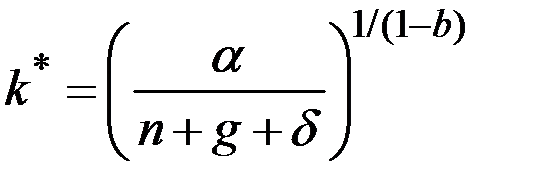Использовав эту зависимость и условие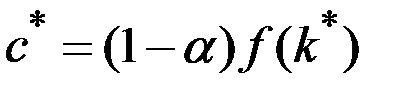 
, получаем уравнение, определяющее потребление в расчёте на единицу эффективного труда на траектории сбалансированного роста:
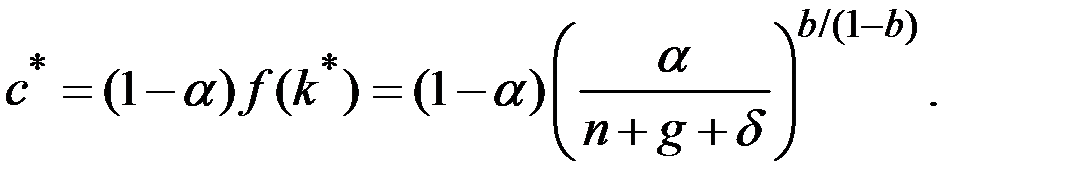
Чтобы определить норму сбережений, соответствующую золотому правилу, найдём максимум этой зависимости по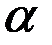 
:
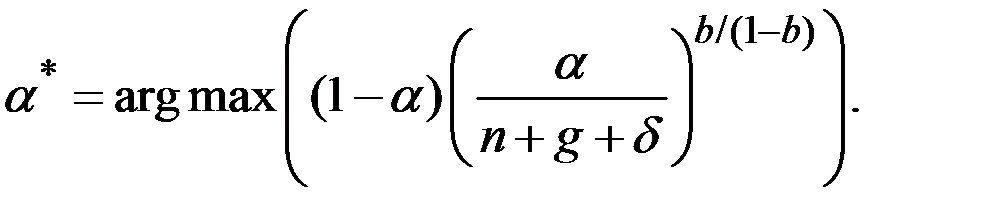
Для этого возьмём производную от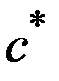 
по :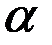
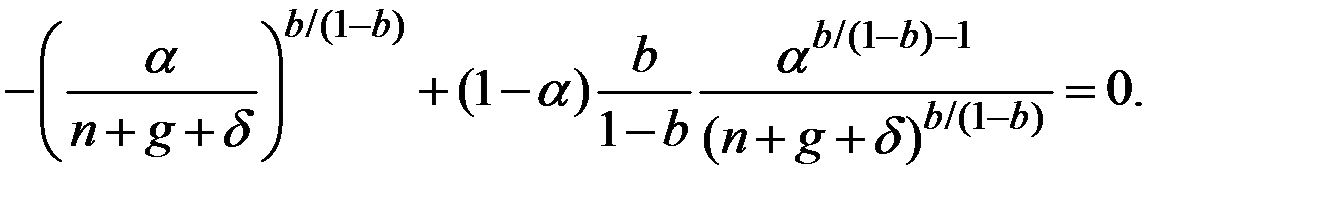
После упрощения получаем оптимальную норму сбережений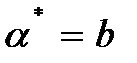 
.
По условию доля дохода капитала в общем доходе равна 1/3, следовательно, эластичность выпуска по капиталу 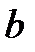тоже равна 1/3, откуда
.
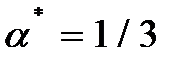Используя эту величину и заданные в условии задачи значения n , g и 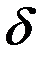, получаем оптимальную капиталовооружённость эффективного труда, соответствующие «золотому правилу:
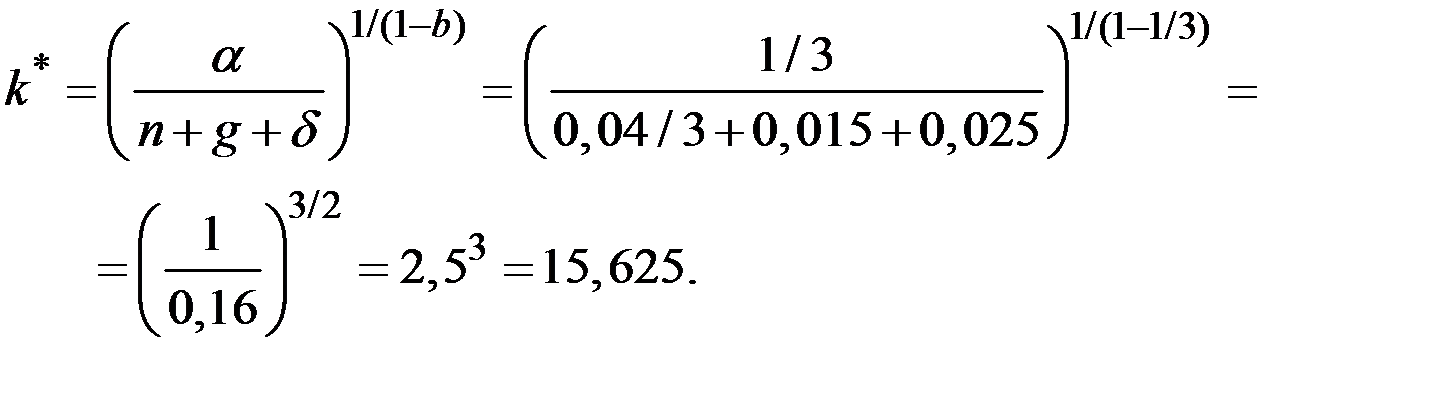
Потребление в расчёте на единицу эффективного труда на траектории сбалансированного роста составит величину:
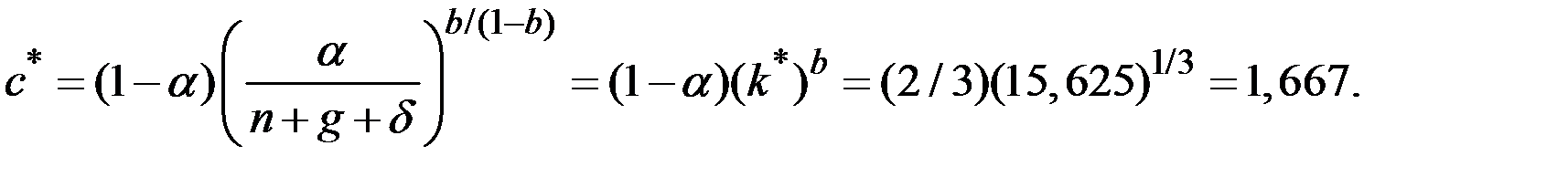
Потребление на единицу работающих составит величину:
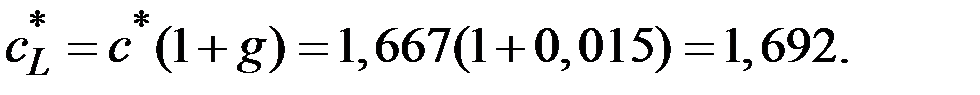
Пример 3.6. Модель Солоу использует функцию ,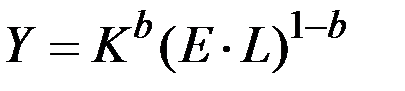
где Y – выпуск, K – капитал, 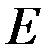– эффективность труда, L – труд, 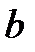– параметр модели. Доля капитала в общем доходе составляет 0,25, темп прироста численности населения равен 2% в год, темп прироста параметра эффективности труда составляет 2,4% в год, а норма амортизации составляет 2% в год, норма сбережений 21,6%. Экономика изначально находится на траектории сбалансированного роста, затем норма сбережений возрастает до 34,3%. Определить потребление на единицу эффективного труда до увеличения нормы сбережений, сразу после увеличения нормы сбережений и в долгосрочном периоде.
Решение. Рассуждая аналогично условиям примера 3.5 получаем оптимальную капиталовооружённость эффективного труда на траектории сбалансированного роста: .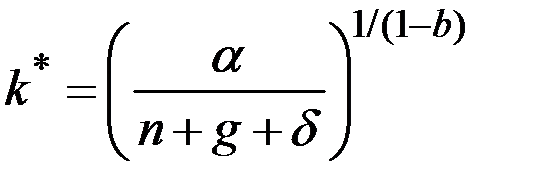
Уравнение, определяющее потребление в расчёте на единицу эффективного труда на траектории сбалансированного роста, имеет вид:
.
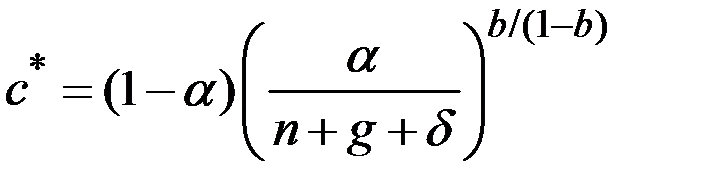1. До изменения нормы сбережений капиталовооружённость эффективного труда и потребление на единицу эффективного труда составляли:
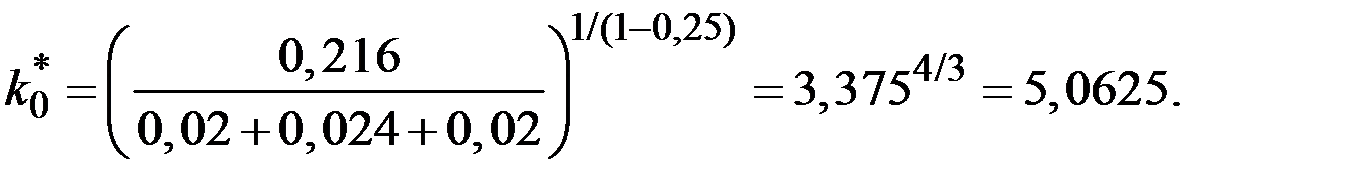
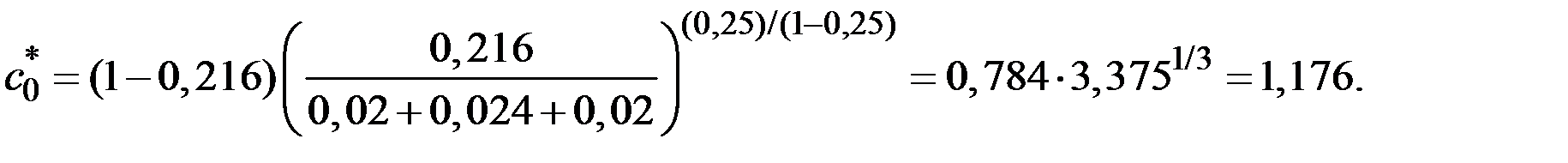
2. Сразу после изменения нормы сбережений капиталовооружённость эффективного труда останется на прежнем уровне, однако норма сбережений уже примет новое значение.
Поэтому потребление будет определяться как новая норма потребления, умноженная на прежний выпуск:
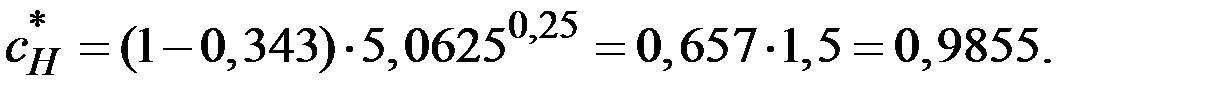
3. В долгосрочном периоде экономика вновь достигнет траектории сбалансированного роста.
Чтобы определить потребление на единицу эффективного труда на новой траектории сбалансированного роста, снова воспользуемся уравнением
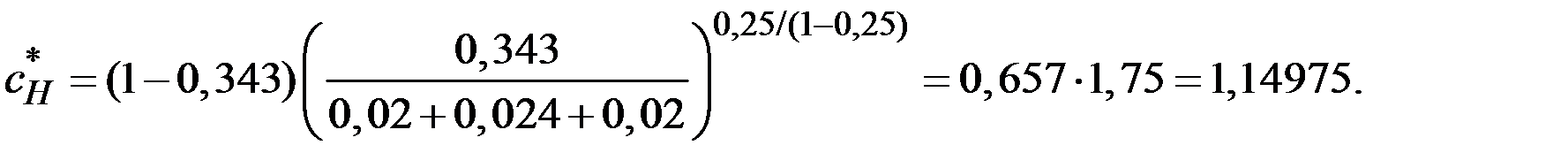
Потребление на единицу эффективного труда до изменения нормы сбережений составляло 1,176, сразу после изменения нормы сбережений снизилось до 0,9855, а в долгосрочном периоде достигло уровня 1,14975.
4. Если новую норму накопления принять по «золотому правилу», т.е.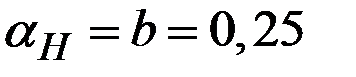 
, то потребление на единицу эффективного труда здесь
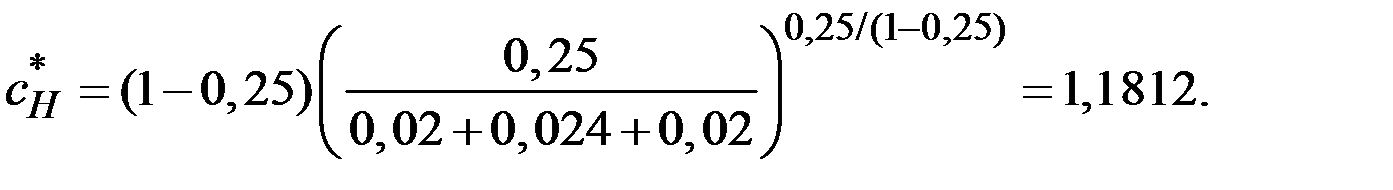
Пример 3.7. Две экономики описываются моделью Солоу с производственной функцией 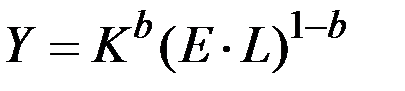, где Y – выпуск, K – капитал, 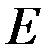– параметр эффективности труда, L – труд, 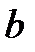– параметр модели. Доля дохода капитала в общем доходе в обеих экономиках составляет 0,5; темп прироста численности населения равен 2% в год; темп прироста параметра эффективности труда составляет 1,5% в год; норма амортизации составляет 2,5% в год. Обе экономики находятся на траектории сбалансированного роста. Определить норму сбережения, потребление на единицу эффективного труда и капиталовооружённость эффективного труда, соответствующие «золотому правилу».
Решение. Рассуждая аналогично решению примера 3.5 получаем оптимальную норму сбережений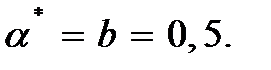 
Используя эту величину и заданные в условии задачи значения n , g и 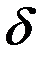, получаем оптимальную капиталовооружённость эффективного труда, соответствующие «золотому правилу:
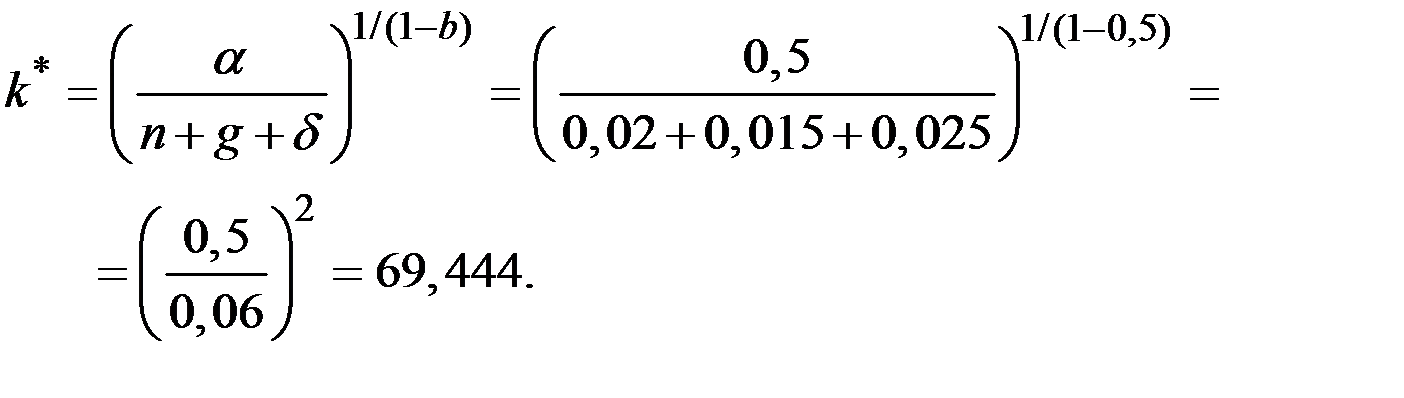
Потребление в расчёте на единицу эффективного труда на траектории сбалансированного роста составит величину:
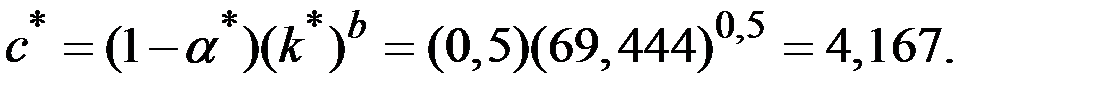
Потребление на единицу работающих составит величину:
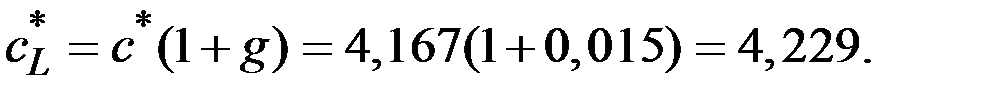
Пример 3.8. Некоторые условия примера 3.7 изменились. В первой экономике норма сбережения стала 25% и потребление на душу населения в этой экономике в 2,5 раза чем во второй. Считая, что потребление на душу населения различается лишь за счёт нормы сбережений, определить, какой стала норма сбережения во второй экономике.
Решение. Рассуждая аналогично условиям примера 3.7 получаем оптимальную капиталовооружённость:
.
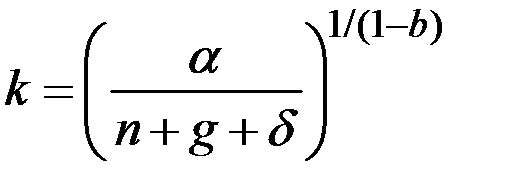Потребление в расчёте на единицу эффективного труда на траектории сбалансированного роста, имеет вид:
.
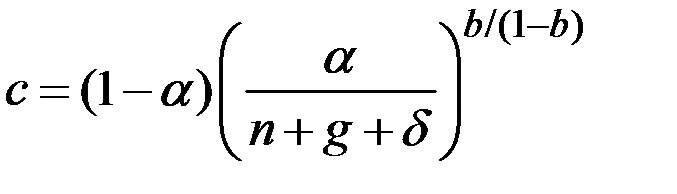По условию задачи, потребление на одного человека должно различаться в 2,5 раза за счёт различий в нормах сбережений.
Имеем соотношение между нормами сбережений:
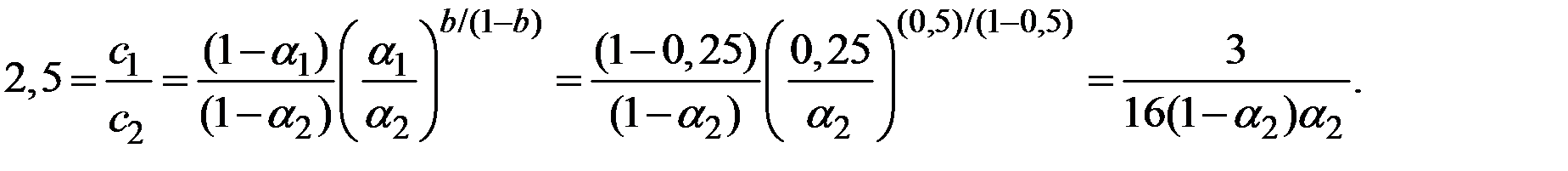
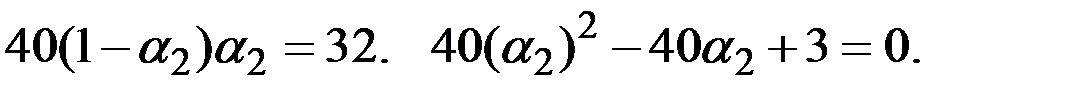
Решив полученное выражение относительно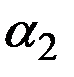 
, получаем:
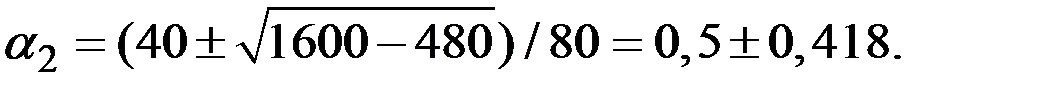
Это соответствует приблизительно значениям 0,082 и 0,918.
Норма сбережения во второй стране может быть 8,2% либо 91,8%.
Пример 3.9. Некоторые условия примера 3.7 изменились. Нормы сбережения одинаковы и равны 0,25. Потребление на душу населения различается между экономиками в 2,5 раза лишь за счёт различий в параметре эффективного труда. Определить, во сколько значение эффективность труда первой экономики выше, чем у второй.
Решение. Если нормы сбережения в обеих странах одинаковы, то объёмы производства на единицу эффективного труда и потребление на единицу эффективного труда также будет одинаковым.
Если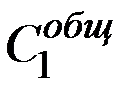 
общее потребление в первой экономике, а 
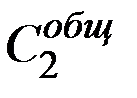– во второй, то имеем соотношение:
.
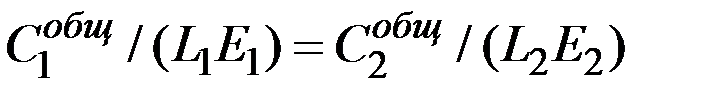Но общее потребление на душу населения в экономиках подчиняется соотношению
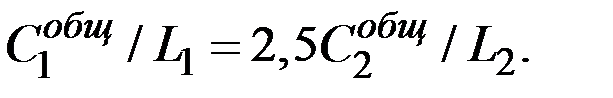
Тогда
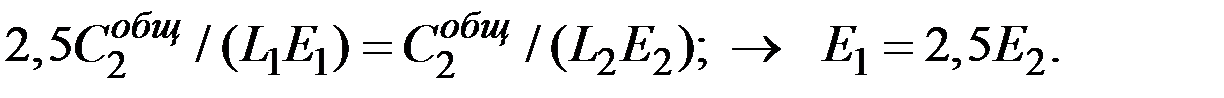
Эффективности труда должны различаться в 2,5 раза.
Дата: 2019-03-05, просмотров: 2205.
