Паутинные модели рынка
Рассмотрим две основные категории рыночных отношений – спрос и предложение. И то и другое зависит от многих факторов, среди которых главный – это цена товара.
Обозначим цену товара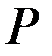 
, объём спроса 
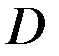, величину предложения 
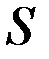(от первых букв английских слов price – цена, demand – спрос, supply – предложение), объём выпуска (производства) продукции 
или 
.
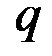При низких (малых) 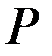имеем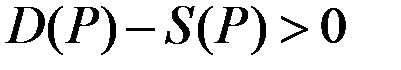 
(спрос превышает предложение), а при больших 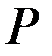, наоборот, 
.
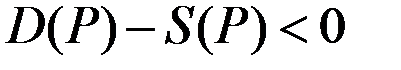Считая функци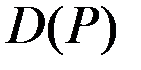и 
и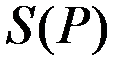 
непрерывными функциями, приходим к заключению, что существует такая цена 
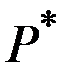, для которой
,
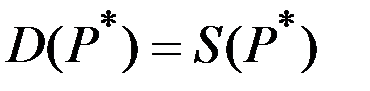т.е. спрос равен предложению.
Цена 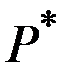называется равновесной, спрос и предложение при этой цене также называются paвновесными.
Установление равновесной цены – одна из главных задач рынка.
Рассмотрим простую модель поиска равновесной цены – так называемую паутинную модель.
Она объясняет феномен регулярно повторяющихся циклов изменения объёмов продажи и цен (например, сельскохозяйственных товаров).
Предположим, что решение о величине объёма производства принимается в зависимости от цены товара в предыдущий период времени.
Так площадь, отводимую под сельскохозяйственную культуру, выбирают в зависимости от её цены, сложившейся в предыдущем году.
Рассмотрим ситуацию, изображённую на рис. 3.2.
Рис. 3.2. Процесс достижения равновесной цены
Пусть в начальной точке предложение товара имеет значение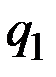 
и выбрано так в зависимости от цены товара 
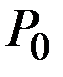в предыдущий период
.
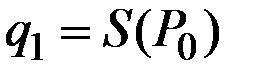Поскольку эта цена больше равновесной, то на кривой спроса 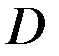ей соответствует объём покупок 
.
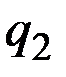Производителю, исходя из такой информации о состоянии рынка, приходится опустить цену товара до величины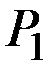 
.
Цена 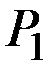ниже равновесной, поэтому на рынке увеличивается спрос до величины 
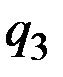. На кривой предложения этой величине соответствует цена предложения 
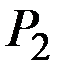и т.д.
В этом случае спираль сходится к точке рыночного равновесия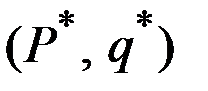 
.
Описанная «спираль» не всегда «скручивается».
В некоторых случаях она может и «раскручиваться», как показывает, например, рис. 3.3.
Сходимость или расходимость описанной выше «спирали» зависит от свойств функци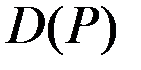й и .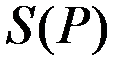
Этот вопрос достаточно сложен.
Ограничимся тем, что укажем лишь название одного из факторов, влияющих на сходимость – так называемая эластичность (спроса, соответственно, предложения).
Рис. 3.3. Расходящийся процесс достижения равновесной цены
3.2.2. Модель Вальраса – это простейшая модель регулирования рынка (поиск равновесной цены) через механизм изменения цен.
Предложение на рынке S ориентировано на спрос D,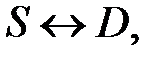 
и в идеале должно быть обеспечено равенство предложения и спроса S = D .
Это равенство достигается через цены.
Если спрос превышает предложение (т.е. D > S), то цены начинают расти до тех пор, пока не будет удовлетворён спрос, т.е. пока D не станет равно S.
Если же предложение превышает спрос (т.е. S > D), то цены начинают падать (снижаться), предложение снижается до тех пор, пока не установится равенство S = D. И процесс повторяется.
Построение модели Вальраса основывается на изучении спроса и предложения на рынке.
Пусть функция спроса D линейная и имеет вид
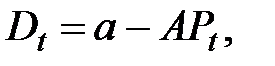
где a, A – постоянные параметры;
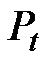– цены на момент времени t.
Пусть функция предложения S также линейная и имеет вид
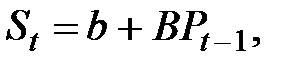
где b, B – постоянные параметры;
Pt – 1 – цены на момент времени t–1.
Обычно при построении функции спроса D ориентируются на текущие цены 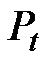, а при построении модели предложения S ориентируются на цены предшествующего периода Pt –1, так как сегодняшнее предложение реагирует на цены с некоторым отставанием во времени.
Построение модели обычно начинают с расчёта количества предлагаемых сделок (предложений) при заданной цене P0:
.
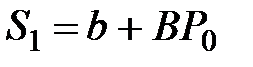Зная количество сделок S1, рассчитывают цену спроса при данном предложении, т.е. спрос приравнивается к предложению D1 = S1 и из функции спроса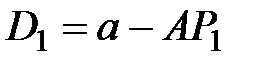 
определяют
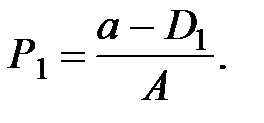
Затем рассчитывают предложение (количество сделок) следующего периода t2, исходя из цены предшествующего периода t1,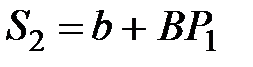 
и цены спроса для t2, принимая, что количество сделок D2 = S2, т.е.
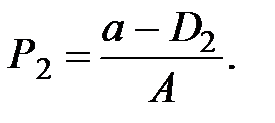
Итерационный расчёт равновесной цены P * целесообразно представить в виде табл. 3.1.
Решение будет закончено, когда цена достигнет равновесия и разница между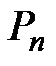 
и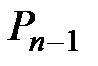 
станет бесконечно малой величиной 
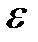, т.е. 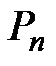практически будет равна .
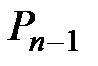Значение цены 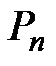= 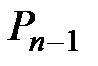называют равновесной ценой
.
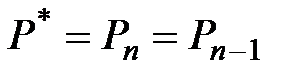Величину равновесной цены можно рассчитать также исходя из равенства
D = S .
Откуда
.
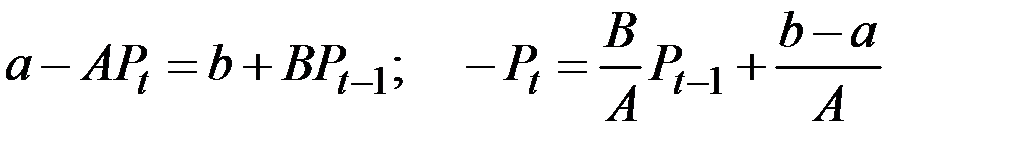При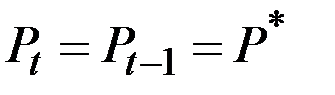 
получаем
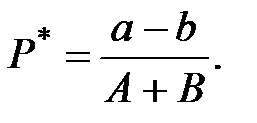
Графическое изображение модели Вальраса имеет вид паутины (рис. 3.4).
Таблица 3.1
Схема расчёта равновесной цены
| t |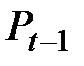 
| 
| 
| 
|
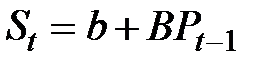
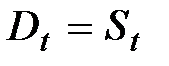
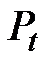
| 1 |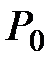 
| 
| 
| 
|
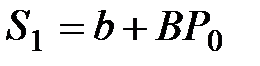
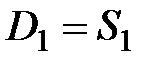
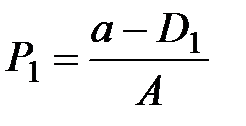
| 2 |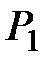 
| 
| 
| 
|
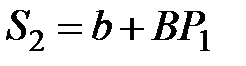
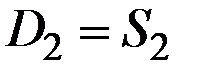
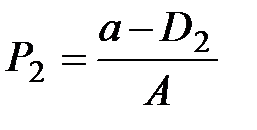
| 3 |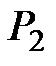 
| 
| 
| 
|
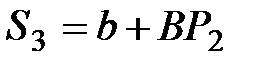
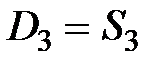
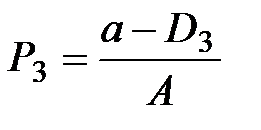
| 4 |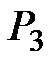 
| 
| 
| 
|
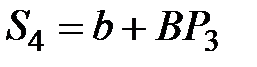
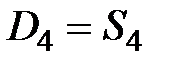
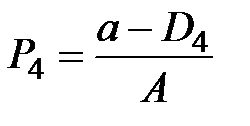
| ¼ | ¼ | ¼ | ¼ | ¼ |
| n – 1 |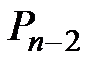 
| 
| 
| 
|
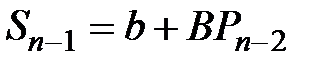
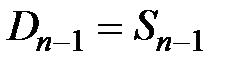
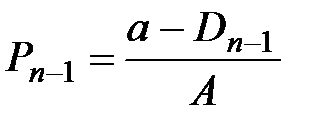
| n |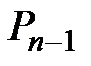 
| 
| 
| 
|
|
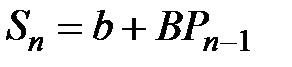
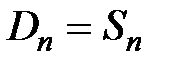
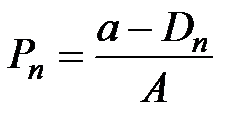
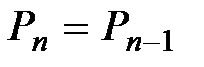
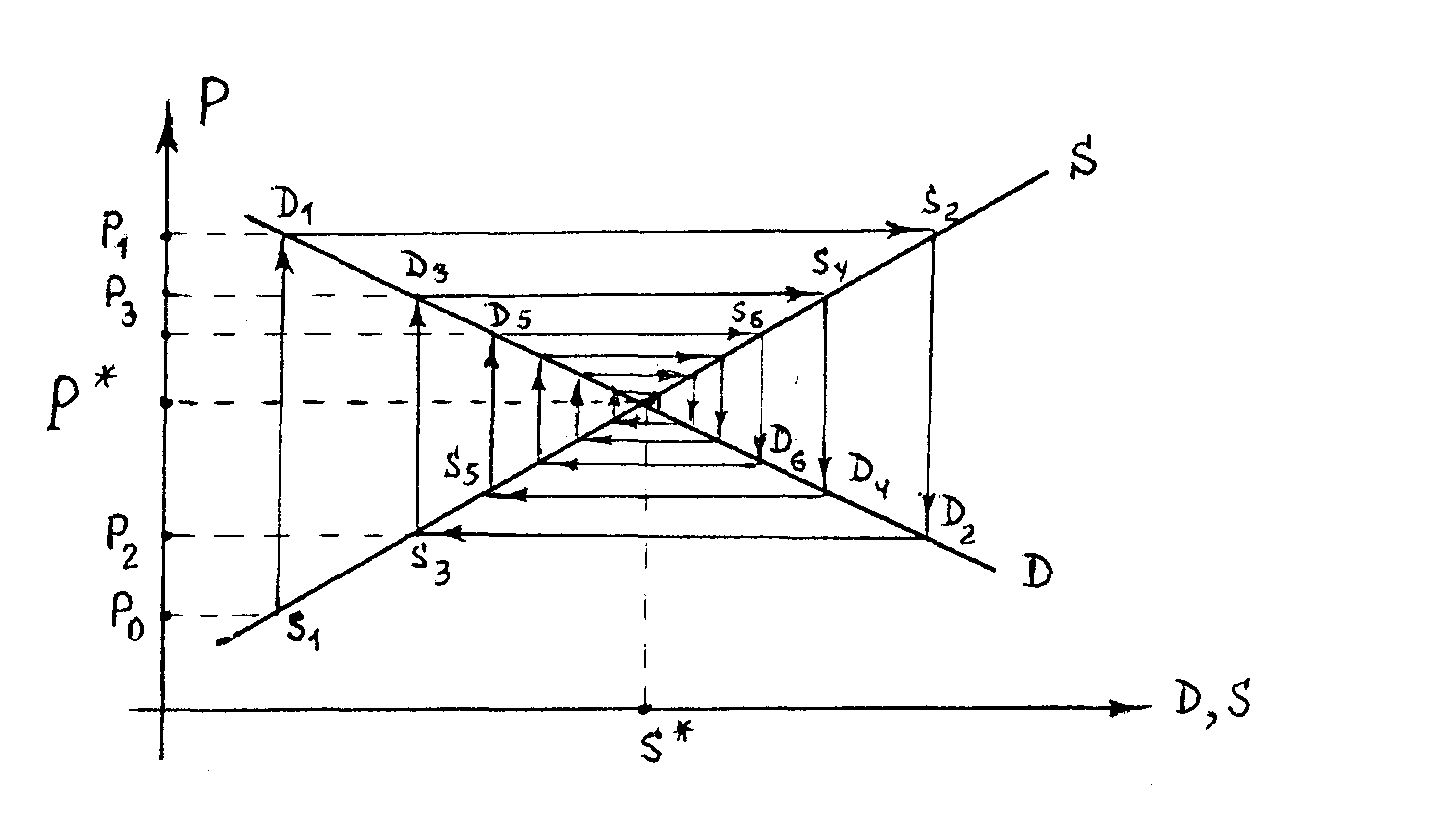
Рис. 3.4. Траектория изменения цен и спроса в модели Вальраса
Точка сходимости паутины является точкой пересечения кривой спроса D и предложения S .
Ей соответствует значение равновесной цены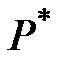 
, при которой устанавливается равновесие количества предложений и спроса.
Дальнейшее увеличение сделок–предложений ведёт к увеличению предложения над спросом, цены начинают падать и торговые сделки становятся убыточными.
Это можно проследить и на графике, и по дальнейшим расчётам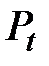 
.
Пример 3.1. Рассмотрим решение задачи расчёта равновесной цены 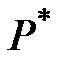на конкретном примере.
Исходные данные имеют следующий вид:
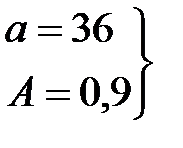для спроса D;
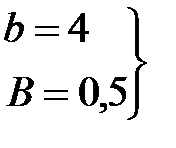для предложения S;
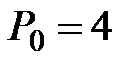первоначальная цена.
Расчёт равновесной цены 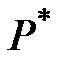представлен в табл. 3.2.
Таблица 3.2
Расчёт равновесной цены
| t |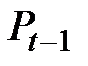 
|
|
|
|
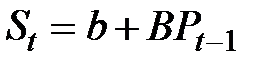
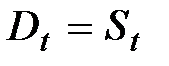
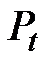
| 1 |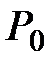 
|  =
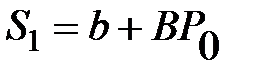= 4 + 0,5×4 = 6
| 
| 
|
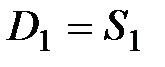
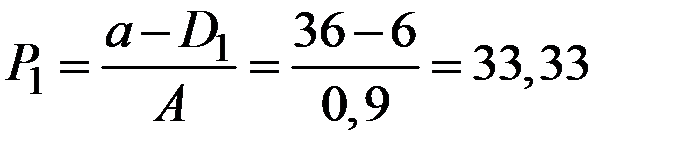
| 2 |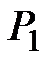 
|  =
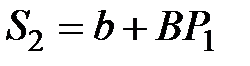= 4 + 0,5×33,33 = 20,67
| 
| 
|
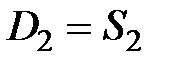
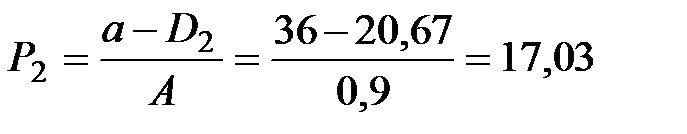
| 3 |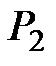
|  =
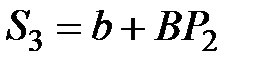= 4 + 0,5×17,03 = 12,52
|
| 
|
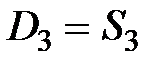
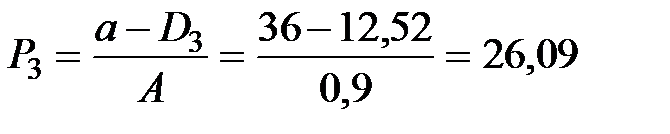
| 4 |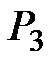
| =
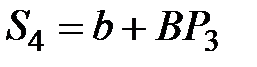= 4 + 0,5×26,09 = 17,05
|
| 
|
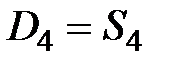
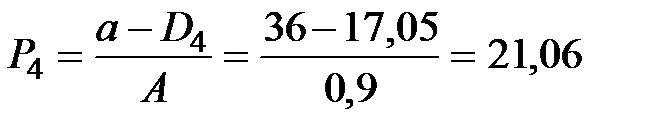
| 5 |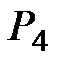 
|  =
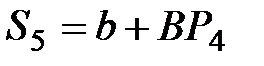= 4 + 0,5×21,06 = 14,53
| 
| 
|
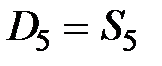
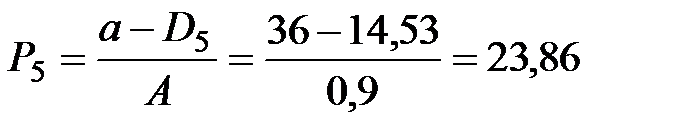
| 6 |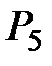 
|  =
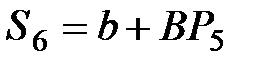= 4 + 0,5×23,86 = 15,93
| 
| 
|
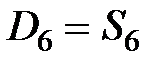
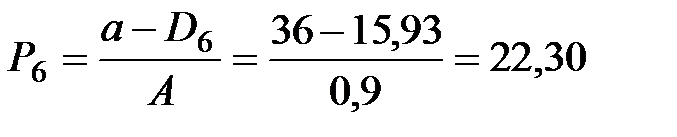
| 7 |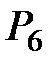 
|  =
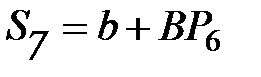= 4 + 0,5×22,30 = 15,15
| 
| 
|
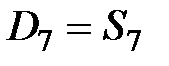
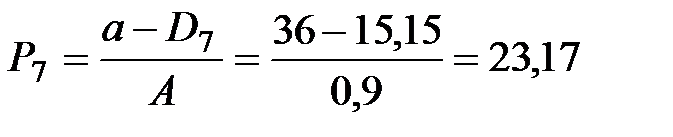
| 8 |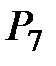 
|  =
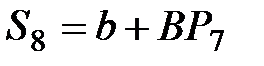= 4 + 0,5×23,17 = 15,59
| 
| 
|
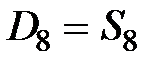
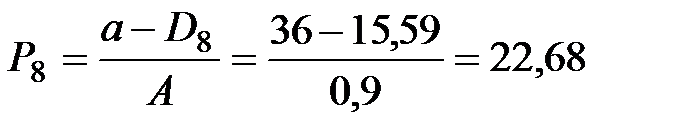
| 9 |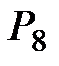 
|  =
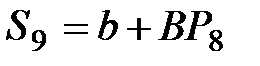= 4 + 0,5×22,68 = 15,34
| 
| 
|
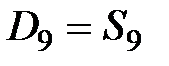
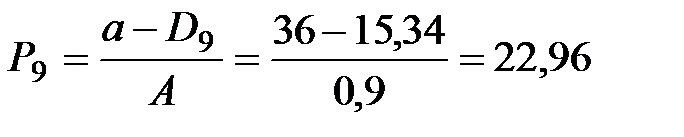
| 10 |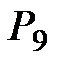 
|  =
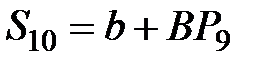= 4 + 0,5×22,96 = 15,48
| 
| 
|
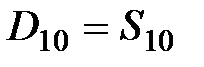
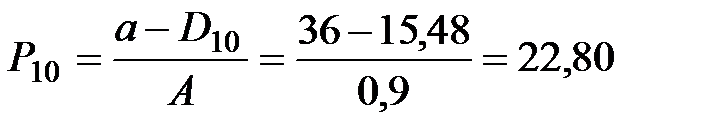
| 11 |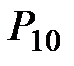 
|  =
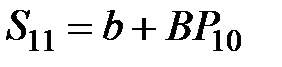= 4 + 0,5×22,80 = 15,40
| 
| 
|
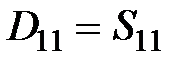
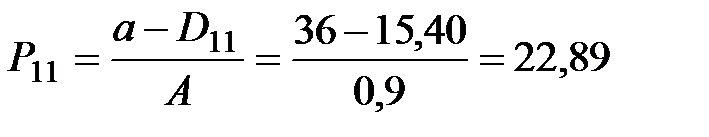
| 12 |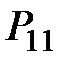 
|  =
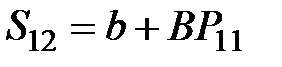= 4 + 0,5×22,89 = 15,45
| 
| 
|
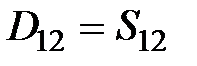
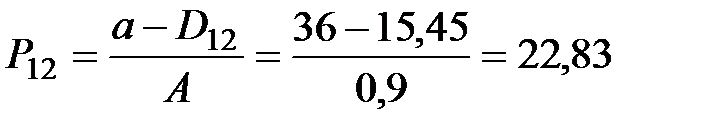
| 13 |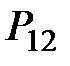 
|  =
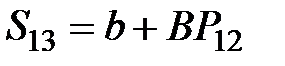= 4 + 0,5×22,83 = 15,42
| 
| 
|
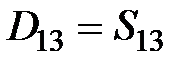
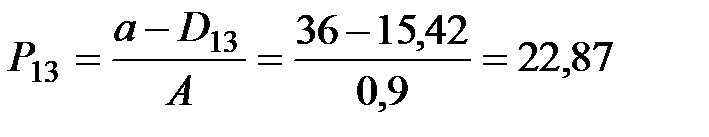
| 14 |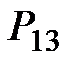 
|  =
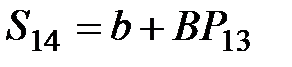= 4 + 0,5×22,87 = 15,44
| 
| 
|
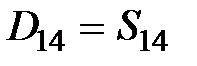
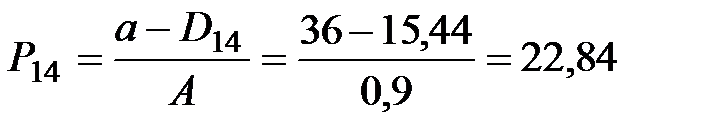
| 15 |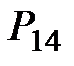 
|  =
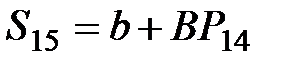= 4 + 0,5×22,84 = 15,42
| 
| 
|
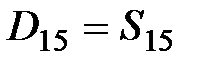
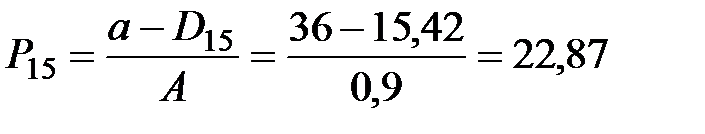
Расчёт равновесной цены можно закончить на 15–й итерации:
.
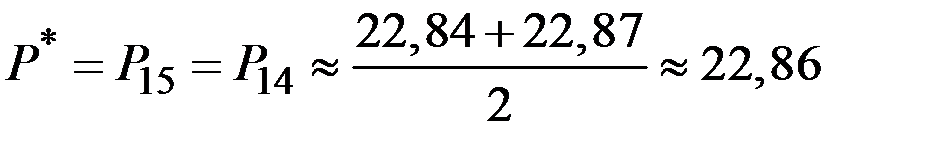Аналогичное значение получаем и по соотношению
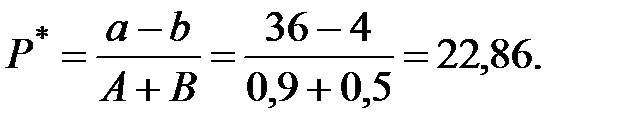
Равновесное количество сделок (предложений) можно определить 2 путями:
1) 
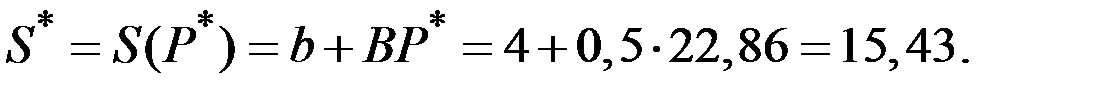
2) 
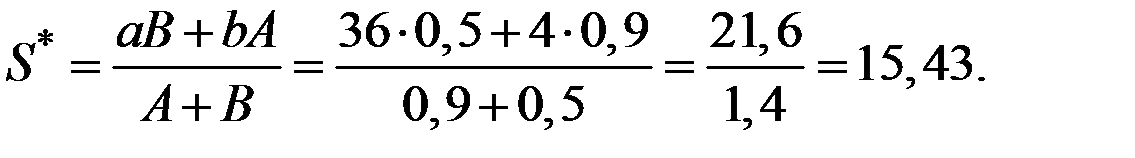
Сделаем некоторые обобщения.
Паутинообразная модель позволяет исследовать (с использованием дискретного подхода к описанию динамики) устойчивость цен и объёмов товаров на рынке, описываемом традиционными кривыми спроса и предложения при наличии запаздывания во времени (лага).
Пусть производители определяют предложение товара в текущем периоде на основе цен, установившихся в предыдущем периоде, то есть
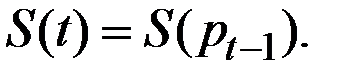
Таким образом, в функцию предложения вклинивается временной лаг продолжительностью в одну единицу времени.
Действительно, решение об объёме производства принимается с учётом текущих цен, но производственный цикл имеет определённую продолжительность, и соответствующее этому решению предложение появится на рынке по окончании данного цикла.
Кривая спроса характеризует зависимость объёма спроса на товар от цены товара в данном периоде, то есть
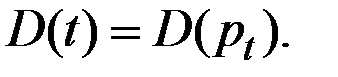
Динамику цены можно описать системой указанных уравнений или одним обобщённым уравнением
.
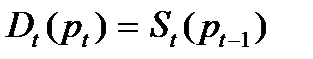Из этого уравнения можно найти значение цены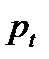 
в текущий момент времени по известному значению 
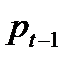в предыдущий момент времени по соответствующей схеме
В качестве частного случая рассмотрим паутинообразную модель, в которой функции спроса и предложения линейны:
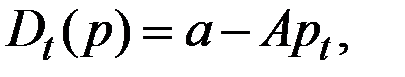
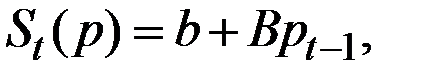
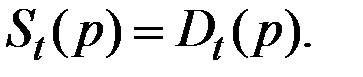
Здесь:
B > 0, так как функция предложения возрастающая;
А > 0, так как функция сброса убывающая;
а > b > 0, то есть
D(0) > S(0) > 0
(считаем, что при нулевой цене спрос превышает предложение).
Уравнение, описывающее динамику такой системы, имеет вид
,
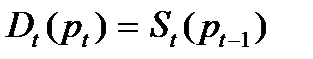или
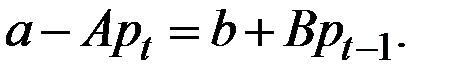
Найдём сначала равновесную цену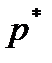 
и равновесный объём производства (предложения) 
.
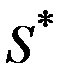Они должны удовлетворять уравнениям
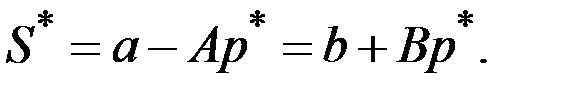
Отсюда
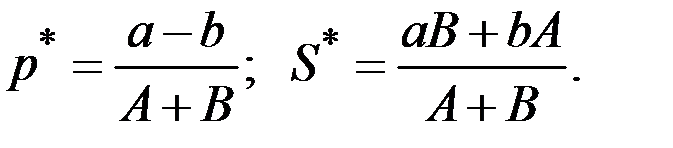
Исследуем поведение цен и объёмов производства в том случае, если начальная точка не совпадает с равновесной.
Вначале эту задачу можно решить графически, получив рисунок типа "паутины", подтверждающий её название.
Задав некоторое первоначальное количество товара и цену, не совпадающие с точкой равновесия, будем последовательно наносить точки в соответствии с процедурой расчёта по модели, соединяя их горизонтальными или вертикальными прямыми линиями.
Из графического анализа (рис. 3.5) можно получить следующие результаты.
1. Если кривая предложения S наклонена круче, чем кривая спроса D, то равновесие на таком рынке будет устойчивым (рис. 3.5.а).
2. Если кривая спроса D наклонена круче, чем кривая предложения S, то равновесие на рынке будет неустойчивым (рис. 3.5.б).
3. При равном наклоне кривых спроса и предложения цены на рынке будут испытывать регулярные колебания с постоянной амплитудой (рис. 3.5.в).
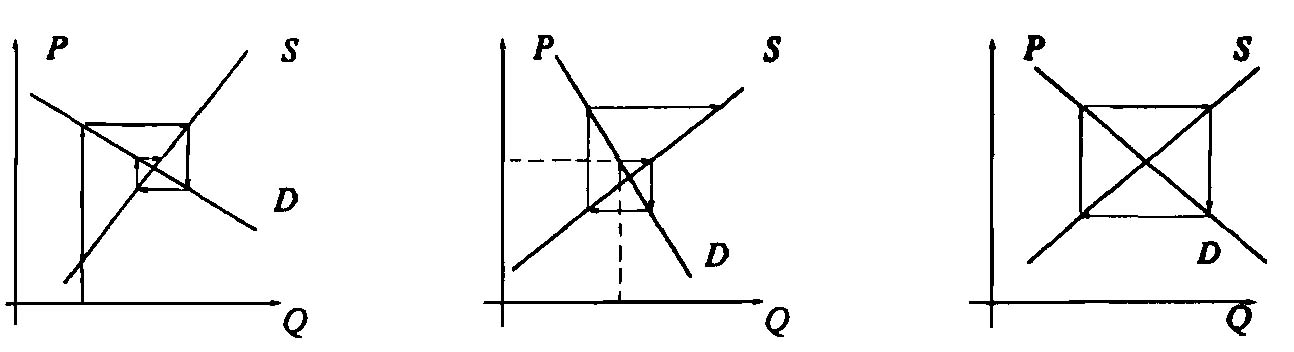
а) б) в)
Рис. 3.5. Условия существования равновесной точки рынка
Теперь перейдём к формальному анализу паутинообразной модели.
Выражая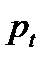 
через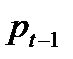 
, имеем следующее рекуррентное соотношение
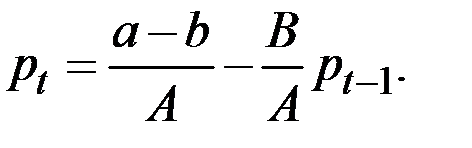
Последовательно применяя это соотношение, находим
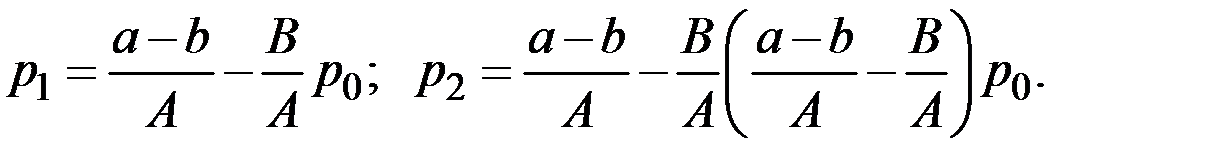
Или в общем виде
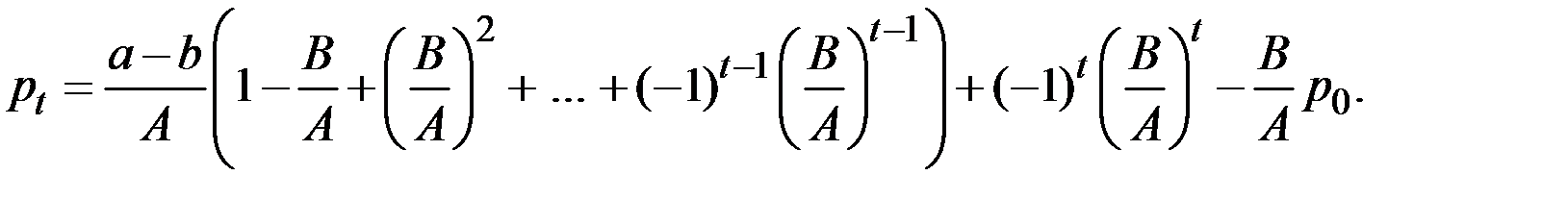
Выражение в скобках есть сумма геометрической прогрессии:
.
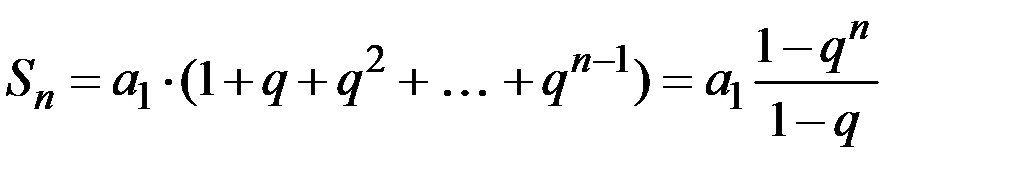Если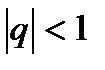 
, то
.
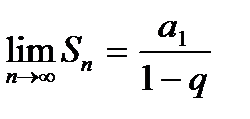Для паутинообразной модели
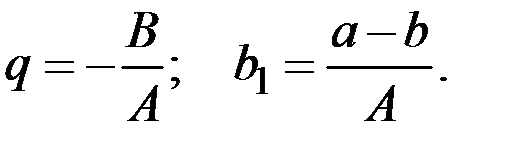
Отсюда получаем выражение для цены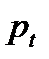 
в произвольный момент времени t:
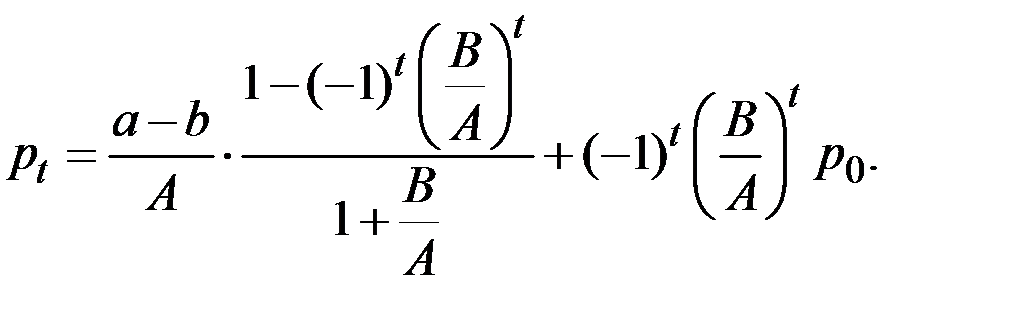
Очевидно, что при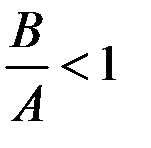 
значение 
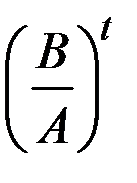стремится к нулю и
.
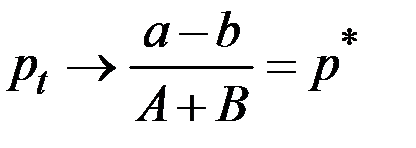То есть при более крутом наклоне кривой предложения S, чем кривой спроса D, равновесие является устойчивым.
Если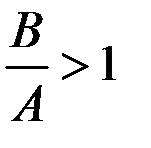 
, то есть более крутой является кривая спроса D, то
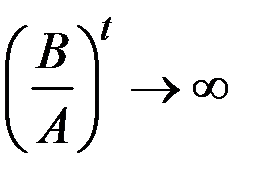
и процесс расходится (равновесие неустойчиво).
При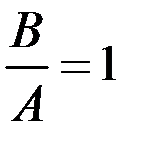 
, то есть при В = А, значения 
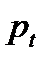чередуются вокруг равновесного значения.
Итак, определяющим моментом для устойчивости системы является менее сильная, сглаживающая реакция на изменения цены той функции, которая имеет временной лаг (функция предложения S).
В реальности при 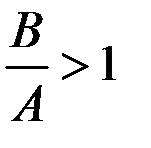бесконечно возрастающих колебаний, конечно, не будет, так как при больших отклонениях от равновесия линейное приближение становится нереалистичным.
В более реалистической нелинейной модели устанавливаются нелинейные колебания большой, но конечной амплитуды, которые являются прообразом экономических циклов подъёма и спада производства.
Модель Самуэльсона
Модель Самуэльсона моделирует связь между изменением цены Р и неудовлетворённым спросом и имеет вид:
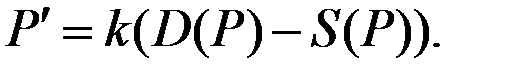
Здесь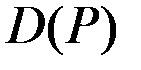 
и 
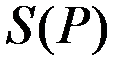– соответственно величины спроса и предложения при цене Р, 
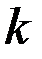– коэффициент.
Предположим, что спрос и предложение задаются линейными функциями цены
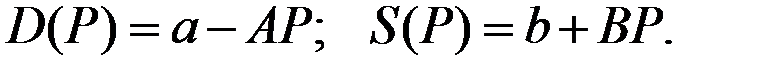
где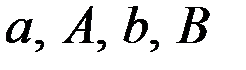 
– некоторые положительные числа.
С учётом этого уравнение Самуэльсона примет вид
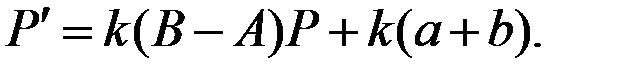
Это уравнение является линейным неоднородным дифференциальным уравнением.
Найдём решение соответствующего ему однородного уравнения.
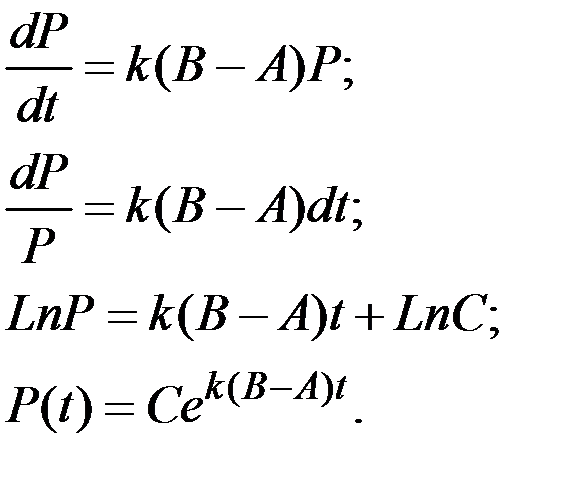
Частным решением уравнения является стационарное равновесное решение Р(t) =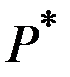 
= const, где 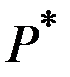– корень уравнения 
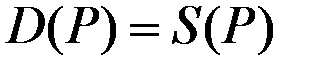(в этом случае обе части дифференциального уравнения будут равны нулю).
Нетрудно определить, что
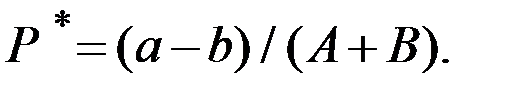
Общее решение уравнения примет вид
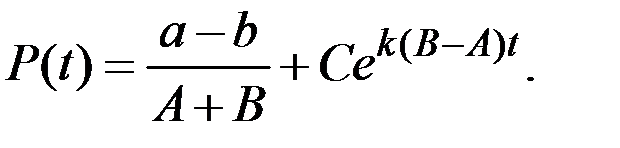
Отсюда следует, что если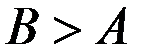 
, то с течением времени интегральные кривые будут отдаляться от состояния равновесия .
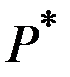Если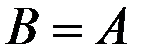 
, то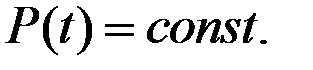 
Если же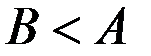 
, то с течением времени интегральные кривые будут асимптотически приближаться к состоянию равновесия .
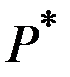Данную модель можно рассматривать как непрерывный аналог паутинной модели рынка.
Модель Харрода–Домара
В качестве примера модели макроэкономической динамики с непрерывным временем рассмотрим модель Харрода–Домара.
Модель описывает динамику дохода Y(t), который рассматривается как сумма потребления С(t) и инвестиций I(t):
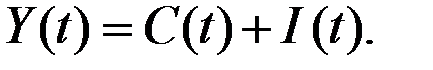
Экономика считается закрытой, поэтому чистый экспорт равен нулю, а государственные расходы в модели не выделяются.
Основная предпосылка модели роста – формула взаимосвязи между инвестициями и скоростью роста дохода.
Предполагается, что инвестиции пропорциональны скорости роста дохода (и наоборот):
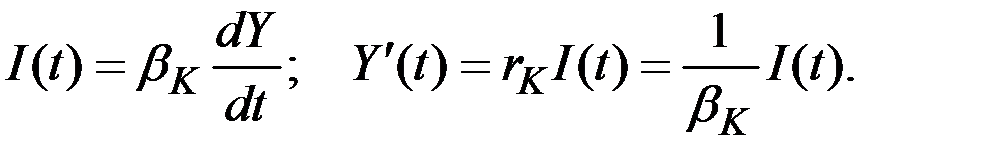
Здесь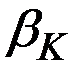 
– коэффициент капиталоёмкости (акселератор) прироста дохода, или приростной капиталоёмкости (обратная величина называется приростной капиталоотдачей, темп прироста дохода от инвестиций 
).
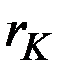В модель включаются следующие предпосылки:
1) инвестиционный лаг равен нулю: инвестиции мгновенно переходят в прирост капитала.
Формально это означает, что
,
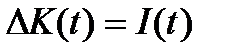где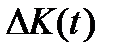 
– непрерывная функция прироста капитала во времени;
2) выбытие капитала отсутствует;
3) производственная функция в модели линейна; это вытекает из пропорциональности прироста дохода приросту капитала:
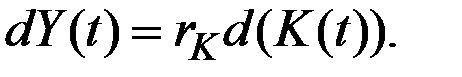
Этим свойством обладает линейная производственная функция
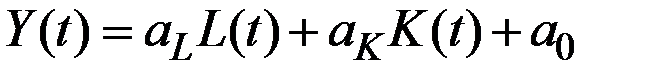
в случае, если либо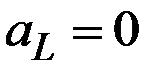 
, либо 
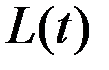= const.
Тем самым следующая предпосылка такова:
4) затраты труда постоянны во времени либо выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом;
5) модель не учитывает технического прогресса.
Перечисленные предпосылки, конечно, огрубляют описание динамики реальных макроэкономических процессов, делают затруднительным применение данной модели, например, для непосредственного расчёта или прогноза величины совокупного выпуска или дохода.
Но её относительная простота позволяет более глубоко изучить взаимосвязь динамики инвестиций и роста выпуска, получить точные формулы траекторий рассматриваемых параметров при сделанных предпосылках.
Зависимость, связывающая между собой во времени показатели инвестиций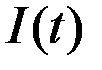 
, определяемый ими объём основного капитала 
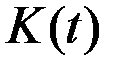и уровень выпуска (дохода) 
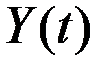, является базовой во всех моделях макроэкономической динамики.
Кроме того, в этих моделях необходимо определить принципы формирования структуры выпуска (дохода) и распределения его между составляющими, прежде всего – между потреблением и накоплением.
Эти принципы могут основываться на оптимизационном подходе (обычно это максимизация совокупных объёмов потребления в той или иной форме), экстраполяционном, равновесном и других.
В рассматриваемой модели предполагается, что динамика объёма потребления С(t) задаётся экзогенно.
Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом прироста или иметь какую–либо другую динамику (в первых двух случаях более просто получить решение модели).
Рассмотрим три варианта модели.
1. Простейший вариант модели получается, если считать
С(t) = 0.
Этот случай совершенно нереалистичен с практической точки зрения (нет потребления), однако в нём все ресурсы направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста. В этом случае получаем динамическое уравнение экономического роста:
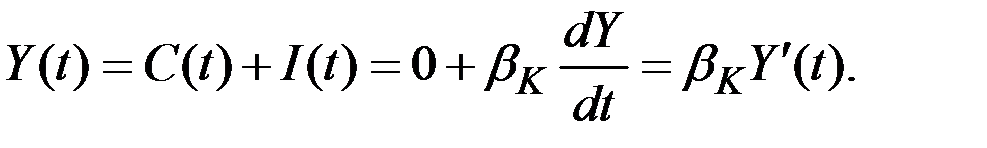
Это – линейное однородное дифференциальное уравнение, и его решение имеет вид
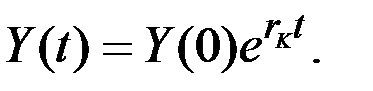
Непрерывный темп прироста (капиталоотдача) здесь равен
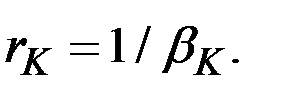
Это максимально возможный (технологический) темп прироста.
2. Пусть теперь потребление постоянно во времени С(t) = C.
Получаем неоднородное линейное дифференциальное уравнение
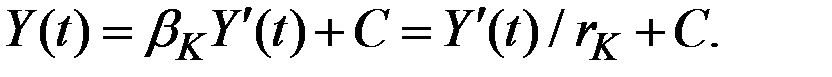
Его частным решением является Y(t) = С, и складывая его с общим решением однородного уравнения
,
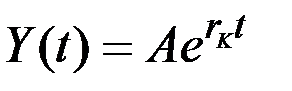получаем общее решение неоднородного уравнения
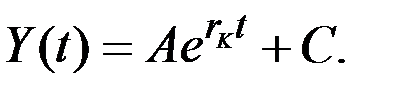
Отсюда, подставив t = 0, имеем:
А = Y(0) – С = I(0)
и динамическое уравнение экономического роста имеет вид:
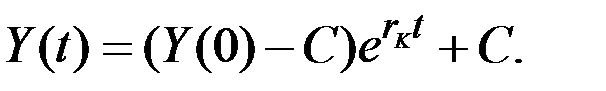
Непрерывный общий темп прироста дохода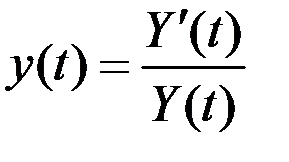 
в этом решении равен
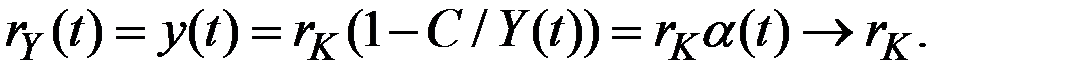
Он составляет величину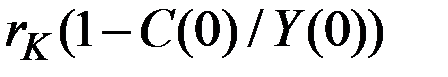 
в начальный момент времени (t = 0) и, возрастая, стремится к 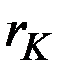при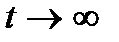 
(доход растёт, а постоянный объём потребления С составляет всё меньшую его долю).
Величина в скобках
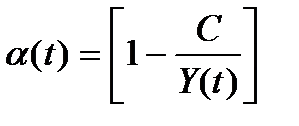
есть норма накопления в момент времени t.
Темп прироста дохода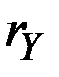 
оказывается пропорциональным этой величине, как и показателю приростной капиталоотдачи .
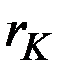При прочих равных условиях рост нормы накопления пропорционально увеличивает темпы прироста дохода.
В то же время это снижает уровень текущего потребления, и для разрешения проблемы согласования конкурентных целей увеличения темпов роста и уровня текущего благосостояния в модель обычно включают элементы оптимизации.
В этом случае решается оптимизационная задача на максимум общего объёма потребления за конечный или бесконечный период времени.
Для отражения предпочтительности более раннего получения результата в модель включается временное дисконтирование, при котором более ранний результат учитывается в критерии с большим "весом".
3. Рассмотрим вариант модели с показателем потребления C(t), растущим с постоянным темпом прироста потребления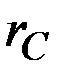 
:
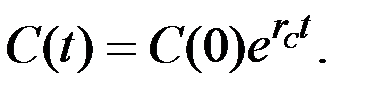
Дифференциальное уравнение этой модели имеет вид:
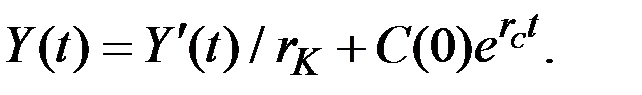
Решение этого уравнения имеет вид:
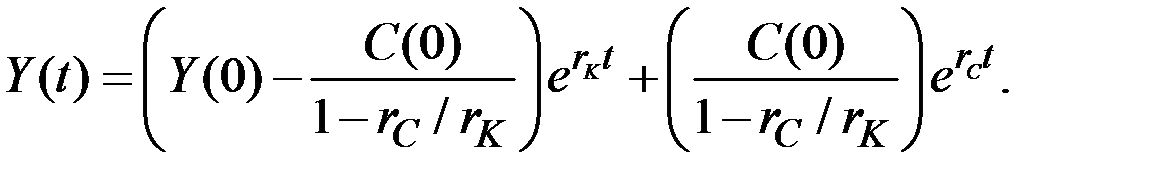
Из общих соображений ясно, что темп прироста потребления 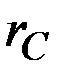не должен быть больше максимально возможного темпа прироста дохода от инвестиций (капиталоотдачи) 
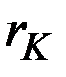, так как иначе потребление будет занимать всё большую и в конце концов – подавляющую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход.
Ясно это и из формулы решения модели, поскольку в случае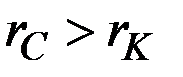 
коэффициент 
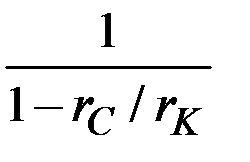отрицателен, а 
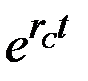растёт быстрее, чем 
.
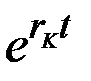Следовательно, второе слагаемое при этом отрицательно и через некоторое время "перевесит" первое.
В решении рассматриваемой модели роста при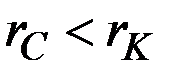 
многое зависит от соотношения между темпами прироста потребления 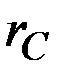и дохода
.
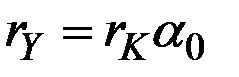Здесь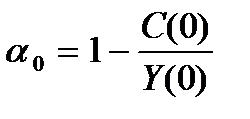 
– норма накопления в начальный момент времени t = 0.
1. Если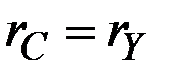 
, то темп прироста дохода равен темпу прироста потребления, и решением является
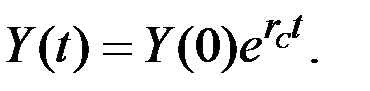
Норма накопления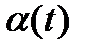 
в этом случае постоянна во времени и равна 
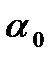, а темп прироста дохода пропорционален норме накопления 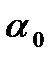и капиталоотдаче .
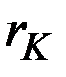Именно эта модификация модели экономического роста, в которой постоянна норма накопления называется моделью Харрода–Домара.
2. Если в рассматриваемой модели роста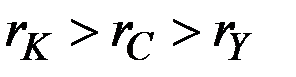 
, то требуемый темп прироста потребления оказывается слишком высоким для экономики. В этом случае коэффициент 
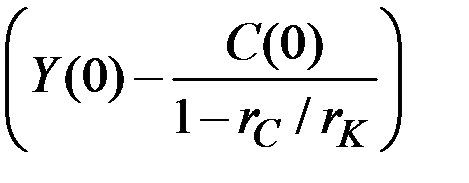отрицателен и, поскольку 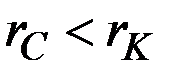, первое, отрицательное слагаемое в решении "перевешивает" в конце концов второе.
Поэтому темп прироста дохода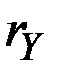 
падает и становится с некоторого момента отрицательным.
Через некоторое время сам доход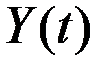 
становится равным нулю, после чего модель теряет экономический смысл.
Это аналогично случаю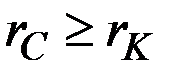 
, хотя здесь уже дело не в том, что нужный темп прироста потребления в принципе недостижим за длительный период.
В данном случае слишком низкой оказывается начальная норма накопления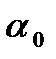 
.
3. Если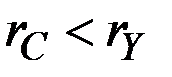 
, то норма накопления, а вместе с ней и темп прироста дохода 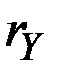растут, причём последний в пределе приближается к .
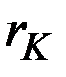Однако в этом случае происходит "накопление ради накопления", ибо потребление растёт заданным темпом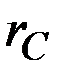 
, а темп прироста дохода 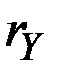удаётся увеличить за счёт более быстрого роста инвестиций.
Норма накопления 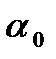здесь превышает 
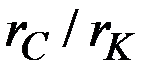, и если исходить из задачи максимизации объёма потребления, то эта норма слишком высока.
Более высокий её уровень требует увеличения инвестиций I(0) за счёт сокращения потребления С(0) в начальный момент, что при фиксированном темпе прироста потребления 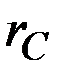обусловливает более низкий его уровень на всей траектории.
В то же время нужный темп прироста потребления 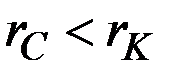можно поддерживать при
.
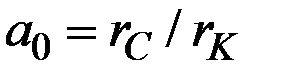Таким образом, если требуется поддерживать постоянный темп прироста потребления 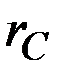, не превышающий технологического темпа, то для максимизации объёма потребления за любой период нужно установить начальную норму накопления
.
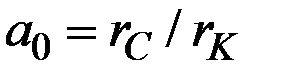Более сложен вопрос о том, какой уровень темпа прироста потребления 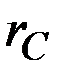более предпочтителен.
Большая его величина позволяет обеспечить больший объём потребления за длительный период, но это происходит за счёт сокращения потребления на начальном этапе.
Таким образом, для выбора значения 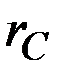(если оно предполагается постоянным) нужна информация о межвременных предпочтениях лица, принимающего решение.
Пример 3.2. Капиталоотдача и норма накопления в модели Харрода–Домара считаются постоянными и равными, соответственно, 0,2 и 0,3. Чему равен темп прироста дохода? Через сколько лет фирма удвоит доход?
Решение. Темп прироста дохода в модели Харрода–Домара равен
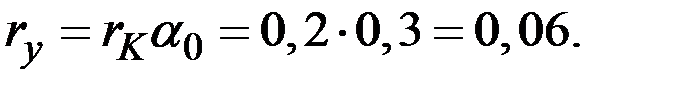
Для удвоения дохода имеем соотношение
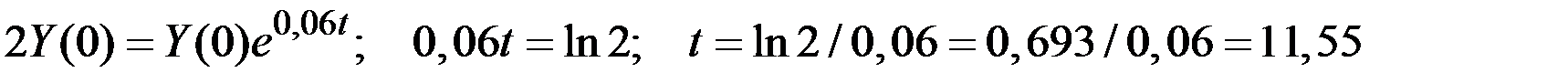лет.
Пример 3.3. Коэффициент капиталоёмкости прироста дохода в модели Харрода–Домара равен 4. Каков максимально возможный темп прироста дохода? Через сколько лет в этой экономике удвоится доход?
Решение. Считаем, что в модели Харрода–Домара потребления нет: С(t) = 0. Тогда динамическое уравнение экономического роста имеет вид:
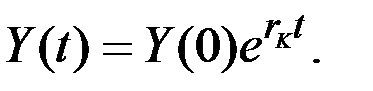
Здесь непрерывный темп прироста дохода (капиталоотдача) равен
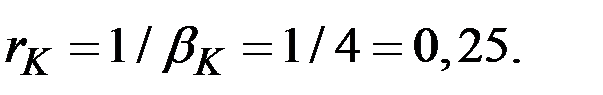
Для удвоения дохода имеем соотношение
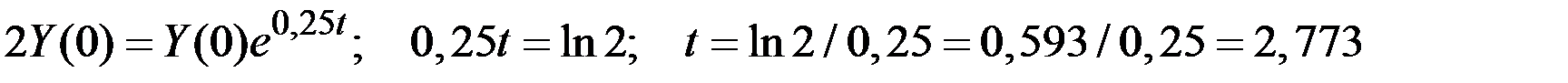года.
Пример 3.4. В экономике некоторой страны равновесие наступило при объёме национального выпуска 6500 млрд. долл. Предельная склонность к потреблению составила 0,8. Коэффициент капиталоёмкости прироста дохода (коэффициент акселерации) равен 2. Определить гарантированный темп прироста дохода согласно модели Харрода–Домара.
Решение. Предельная склонность к сбережению составит величину
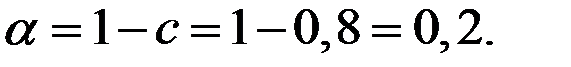
Капиталоотдача (темп прироста дохода от инвестиций) составит величину
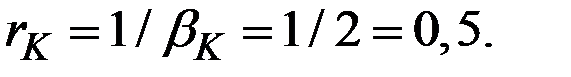
Гарантированный темп прироста дохода составит величину
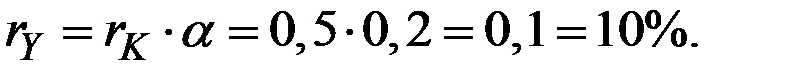
Дата: 2019-03-05, просмотров: 835.
