Равновесие означает такое состояние объекта (системы), которое он сохраняет при отсутствии внешних воздействий.

Задачи экономической динамики включают как описание процессов выхода к состоянию равновесия, так и процессов трансформации самого этого состояния под воздействием внешних сил.

Рассмотрим простую экономическую систему в состоянии равновесия и опишем движение такой системы в непрерывном и дискретном случаях.

В первом случае динамика системы описывается с помощью дифференциального уравнения, во втором – с помощью разностного уравнения.

В непрерывном случае дифференциальное уравнение связывает изменения показателя (если наша система описывается одним показателем x(t), или просто х) со скоростью его движения .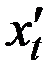

Будем считать, что скорость изменения показателя х пропорциональна величине его отклонения от равновесного значения 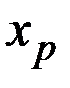, т.е. чем дальше показатель отклонился от равновесного значения, тем быстрее он стремится вернуться к нему.

Если в уравнении присутствует только первая производная х по времени, а сама связь линейна, то это линейное дифференциальное уравнение.

1. Пусть линейное неоднородное дифференциальное уравнение имеет, например, следующий вид (для непрерывного времени):

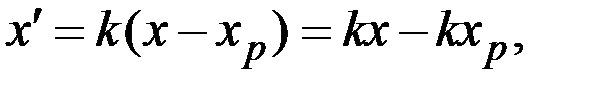
где k – коэффициент пропорциональности.

В этом уравнении 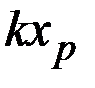 – свободный член.

Без него уравнение 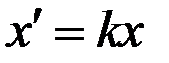 называется однородным и его решение

.

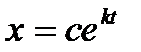Исходное неоднородное уравнение имеет частное решение

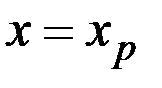
(если величина х находится в состоянии равновесия), а общее решение неоднороднго уравнения есть сумма любого частного решения и общего решения однородного уравнения, то есть

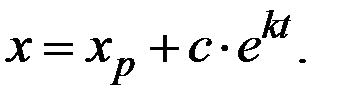
Учитывая, что при t = 0 величина х равна х(0), получаем

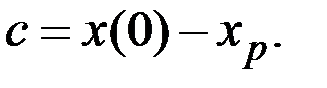
Общее решение исходного неоднородного уравнения имеет вид

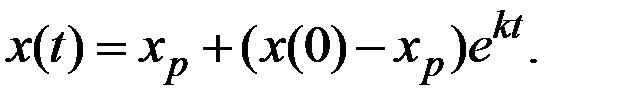
Если k < 0, то 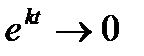 и равновесие устойчиво, то есть при отклонении величины x(t) от значения  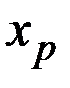она вновь стремится принять это значение (рис. 3.1).

Непрерывное время

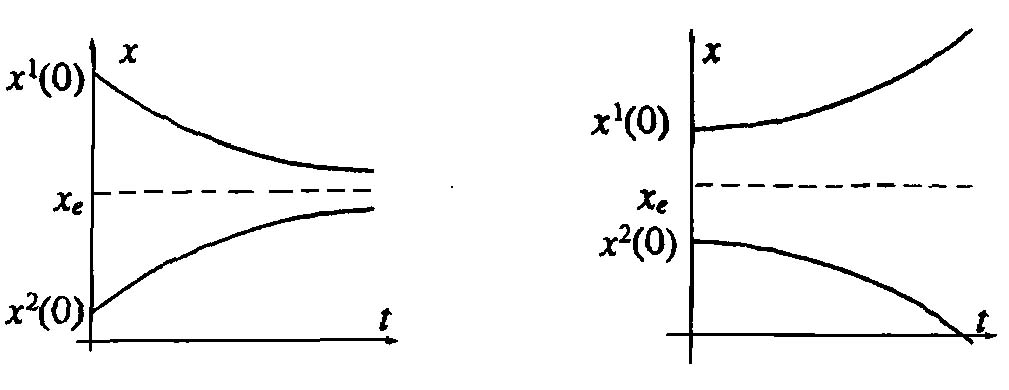
Дискретное время

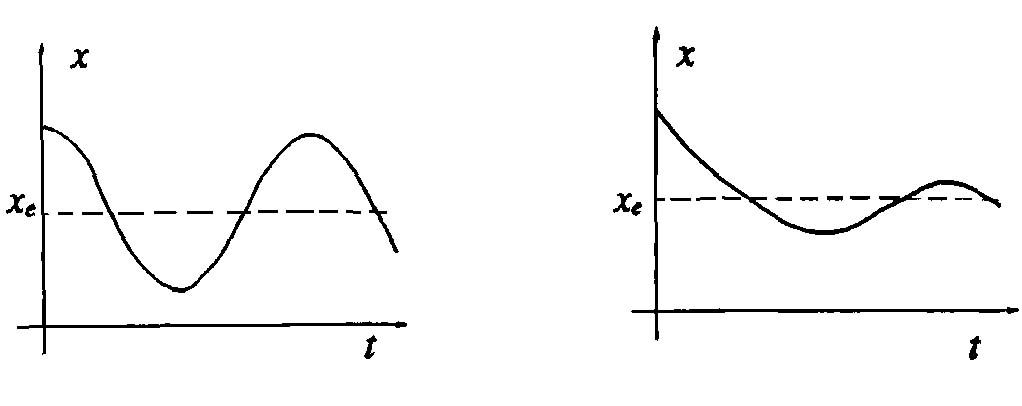
Рис. 3.1. Условия динамического равновесия системы

При k > 0 величина 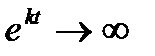 и x(t) стремится к бесконечности (если начальное состояние не совпадает состоянием равновесия).

2. Поведение в дискретном времени может быть описано с помощью разностного уравнения, связывающего величины х в соседние моменты времени, то есть 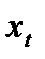 и .

Например, в дискретной ситуации, аналогичной уже описанной, может использоваться разностное уравнение

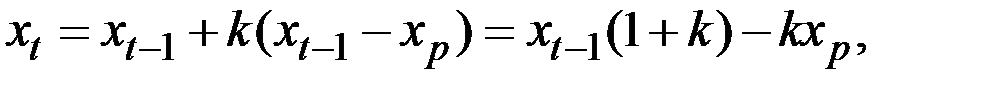
решением которого является

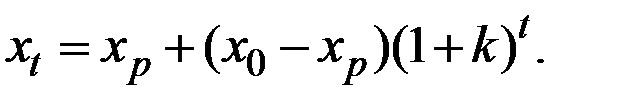
Это решение найдено (аналогично непрерывному случаю) как сумма общего решения

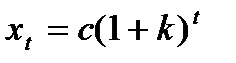
для однородного уравнения

,

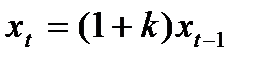и частного решения

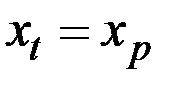
для исходного разностного уравнения (с учётом 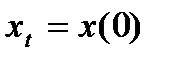 при t = 0).

При k < 0 система в случае уклонения от 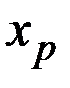 будет двигаться в направлении 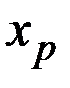, при k > 0 – уходить ещё дальше от него.

Равновесие устойчиво при

– 2 < k < 0

и неустойчиво при

k > 0   или   k < – 2

При k < –1 показатель х каждый раз "перескакивает" равновесное значение 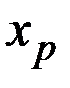, причём при k < – 2 показатель х каждый раз "перескакивает" равновесное значение  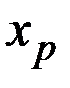слишком далеко, чтобы приблизиться в конце концов к .

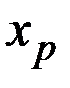При –1  < k < 0 показатель х стремится к состоянию рвновесия 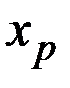 не перескакивая через него.

Ниже приводятся некоторые примеры моделей экономической динамики: модели Вальраса, Самуэльсона, Харрода–Домара, Соллоу.