Динамику показателей экономического объекта характеризуют прежде всего:

1) абсолютные приросты, 2) темпы роста, 3) темпы прироста.

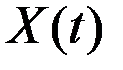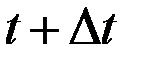Если рассматривается зависящая от времени величина , то абсолютный прирост этой величины от момента  до момента  равен

,

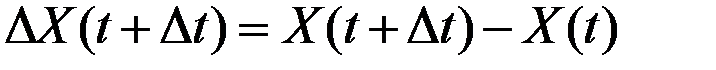дискретный темп роста равен величине (индексу)

,

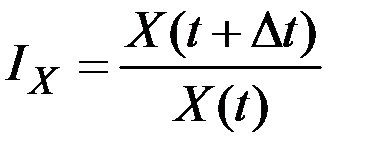дискретный темп прироста равен величине

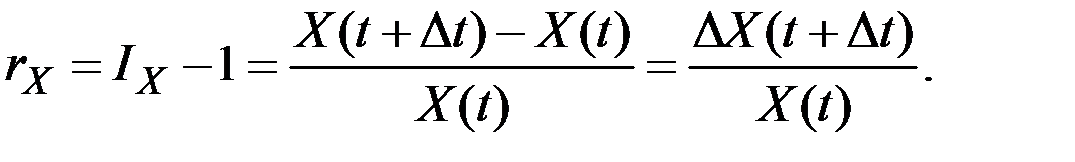
Непрерывный темп роста величины 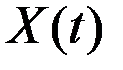 равен значению

.

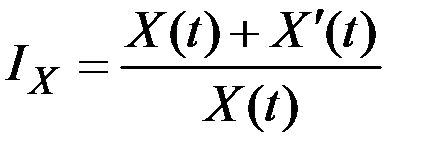Непрерывный темп прироста величины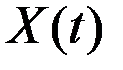

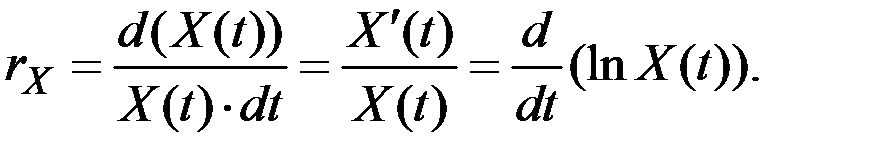
Если темп прироста 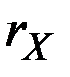 дискретен и неизменен во времени, то динамика показателя  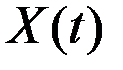может быть описана в виде зависимости

.

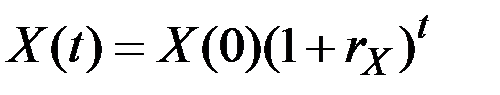Если величина 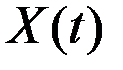 есть непрерывная функция времени, то её рост с непрерывным темпом прироста  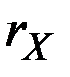записывается в виде

,

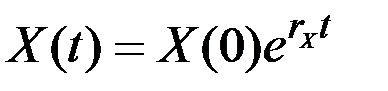где 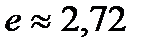 – основание натуральных логарифмов,

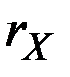 – непрерывный темп прироста.

При росте величины 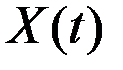 с непрерывным темпом прироста 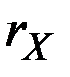дискретный темп роста за один такт времени  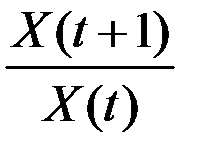равен 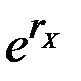, что при малых  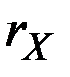близко к (1+ 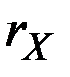), то есть к темпу роста при дискретном темпе прироста .

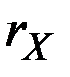Исследуем темпы прироста суммы и произведения двух показателей с различными темпами прироста.

1. Пусть показатель 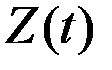 есть сумма показателе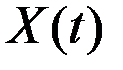й  и 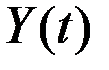, растущих соответственно, с постоянными непрерывными темпам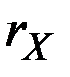и  и 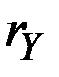, причём 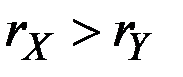. Тогда  

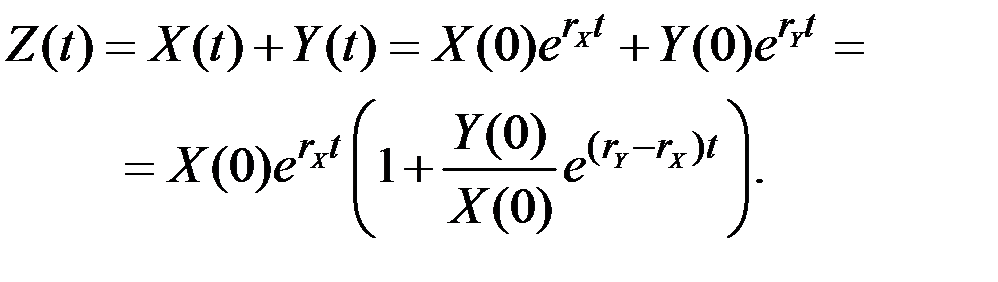
Поскольку 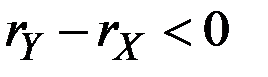, то величина в скобках стремится к единице при 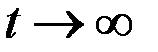, и темп прироста суммы приближается к темпу быстрее растущего составляющего, то есть к .

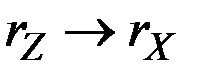2. Сумма показателе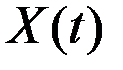й  и 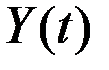, растущих с постоянными дискретными темпам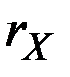и  и 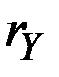, причём  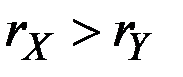описывается зависимостью

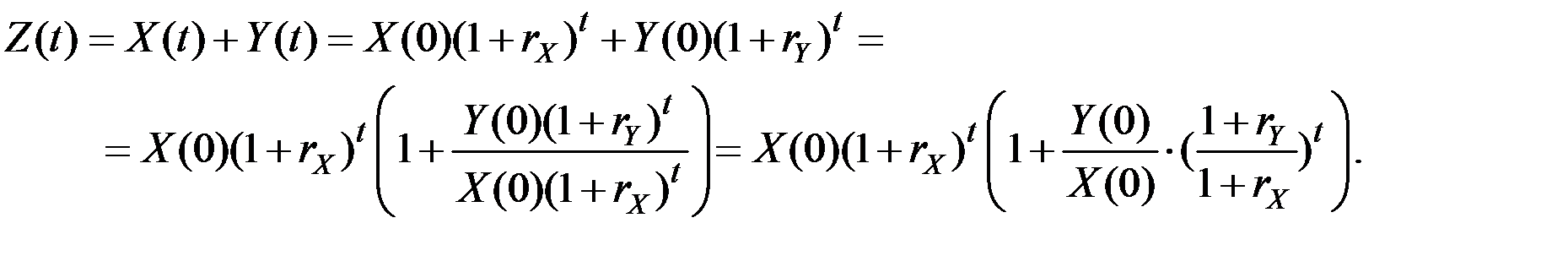
Поскольку 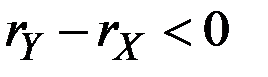, то величина в скобках стремится к единице при 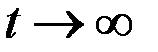, и темп прироста суммы приближается к темпу быстрее растущего составляющего, то есть к .

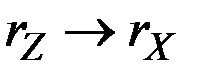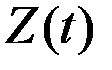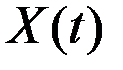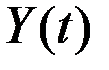3. Пусть величина  есть произведение показателей  и , растущих с постоянными непрерывными темпам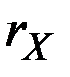и  и 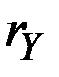. Тогда:

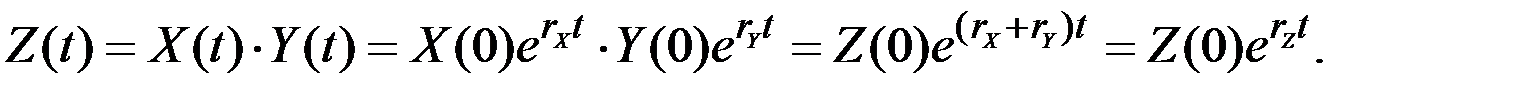
Здесь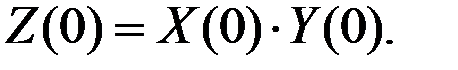

В этом случае темп прироста произведения равен сумме темпов прироста сомножителей: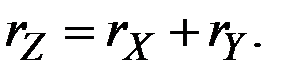

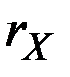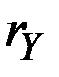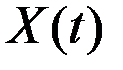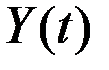4. Если  и  – дискретные темпы прироста  и , то

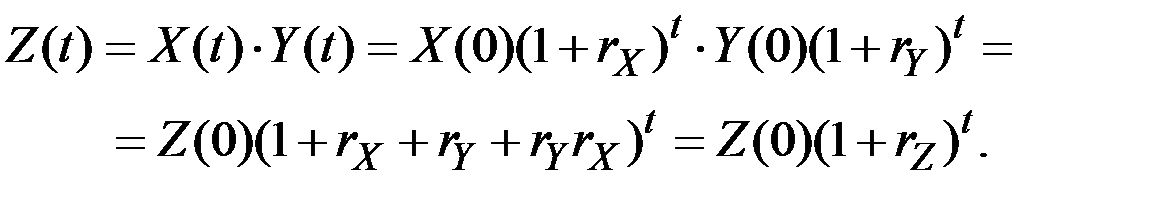
Здесь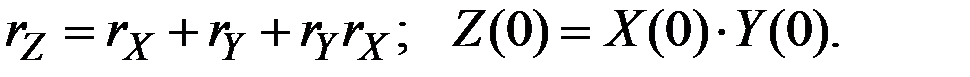

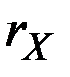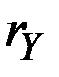При малых  и  величина  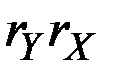пренебрежимо мала, и темп прироста произведения приближённо равен сумме темпов прироста сомножителей. Если же произведение  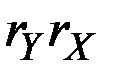значительно, то темп прироста произведения показателей не может приближённо считаться равным сумме темпов прироста сомножителей, поскольку существенно её превышает.

Связь объёмных и темповых (прироста) величин легко продемонстрировать на примере производственной функции.

Пусть:

Y(t), K(t), L(t) – объёмные показатели выпуска продукции, использованного капитала и труда (непрерывные функции времени);

y(t), k(t), l(t) – непрерывные темпы их прироста.

Объёмная производственная функция с нейтральным техническим прогрессом (при постоянном темпе 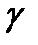) имеет вид

.

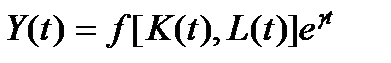Логарифмируя эту зависимость, получаем:

.

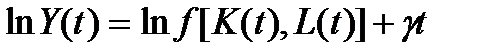Далее дифференцируем по времени:

,

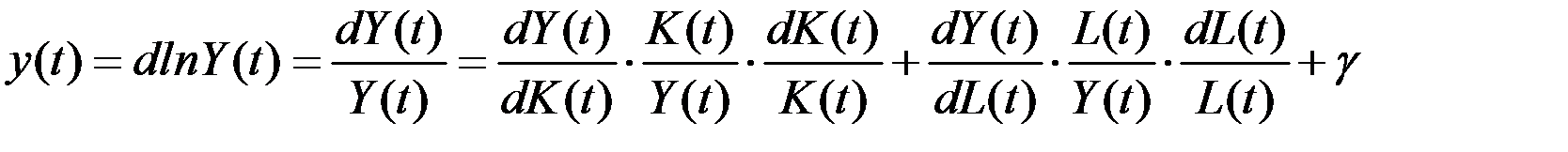то есть,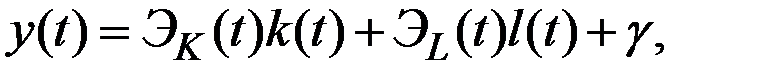         

где 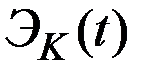 и 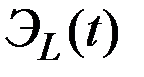 – эластичности выпуска по капиталу и труду соответственно.

Эта линейная формула характеризует вклад темпов прироста факторов производства в общие темпы прироста дохода, а показатель 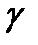 характеризует вклад технического прогресса.